| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
 Postano: 21:33 sri, 12. 5. 2010 Naslov: Postano: 21:33 sri, 12. 5. 2010 Naslov: |
    |
|
|
Si bila na vjezbama cca. 4.5.?. Uglavnom, imas cijeli postupak za takav slican zadatak. Rijesili smo ga na 3 nacina.
a=alfa1 a1 + alfa2 a2 + alfa3 a3
b=v-a
sad trebas naci alfe. Primjeti da b mora biti okomit na M.
Dakle
(b, a1) = 0
(b, a2) = 0
(b, a3) = 0
imas 3 jdbe sa 3 nepoznanice i izracunas alfa1, alfa2 i alfa3
sad te alfe uvrsti u prvu jdbu da izracunas a, pa uvrsti u jdbu ispod i izracunas b
EDIT: naravno, kao sto boris rece, prvo trebas dobiti bazu :oops:
Si bila na vjezbama cca. 4.5.?. Uglavnom, imas cijeli postupak za takav slican zadatak. Rijesili smo ga na 3 nacina.
a=alfa1 a1 + alfa2 a2 + alfa3 a3
b=v-a
sad trebas naci alfe. Primjeti da b mora biti okomit na M.
Dakle
(b, a1) = 0
(b, a2) = 0
(b, a3) = 0
imas 3 jdbe sa 3 nepoznanice i izracunas alfa1, alfa2 i alfa3
sad te alfe uvrsti u prvu jdbu da izracunas a, pa uvrsti u jdbu ispod i izracunas b
EDIT: naravno, kao sto boris rece, prvo trebas dobiti bazu 
_________________
Though your dreams be tossed and blown...
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 12:53 čet, 13. 5. 2010 Naslov: Postano: 12:53 čet, 13. 5. 2010 Naslov: |
    |
|
|
[quote="michelangelo"]evo može objašnjenje 1. zadatka, jel to ide gram-schmidtom i baza mi je p(t) ili se varam???
i pitanje je li u zad. br. 2 dovoljno napraviti ovo: A=B+C, C=A-B gdje A imamo zadan, a B=aA1+bA2 a sad negdje sam u bilježnici vidjela da je asistent ove a i b izračunao kao a=<B|A1> i analogno za b tako bi onda za čas izračunali B i na kraju i C.
http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol2a.pdf[/quote]
u prvom imas polinom p(t)=a+2at+bt^2=a(1+2t)+bt^2, pa je baza {1+2t,t^2}, a onda tu bazu ortonormiras Gram-Schmidtom
u drugom a=<B|A1> vrijedi samo ako je A1 ortonormirana,tako i za A2,pa ih prvo ortonormiraš.
u tom zadatku je dimM=2, pa je dimM^t=7,pa nije baš pametno(bar ja tako nebi) ići načinom da prvo nadopunimo do baze,pa ortonormiramo sve, a niti tražiti bazu za M^t tako da uzmemo da je x E M^t okomit na A1 i A2,pa rješavati sustav.(samo mala opaska :))
najbolje je ovako kako si počeo,ali prije toga ortonormiraj A1 i A2 :wink:
p.s.M^t mi je oznaka za ortogonalnu komplement od M
p.s.s. izgleda da su nešto krivo napisali u zadatku? piše Prikazite matricu A u obliku A = B +C, takoda je A iz M, a B iz M^t. valjda se misli B iz M, C iz M^t..ili?
| michelangelo (napisa): | evo može objašnjenje 1. zadatka, jel to ide gram-schmidtom i baza mi je p(t) ili se varam???
i pitanje je li u zad. br. 2 dovoljno napraviti ovo: A=B+C, C=A-B gdje A imamo zadan, a B=aA1+bA2 a sad negdje sam u bilježnici vidjela da je asistent ove a i b izračunao kao a=<B|A1> i analogno za b tako bi onda za čas izračunali B i na kraju i C.
http://web.math.hr/nastava/la/kolokviji/07-08/la2/kol2a.pdf |
u prvom imas polinom p(t)=a+2at+bt^2=a(1+2t)+bt^2, pa je baza {1+2t,t^2}, a onda tu bazu ortonormiras Gram-Schmidtom
u drugom a=<B|A1> vrijedi samo ako je A1 ortonormirana,tako i za A2,pa ih prvo ortonormiraš.
u tom zadatku je dimM=2, pa je dimM^t=7,pa nije baš pametno(bar ja tako nebi) ići načinom da prvo nadopunimo do baze,pa ortonormiramo sve, a niti tražiti bazu za M^t tako da uzmemo da je x E M^t okomit na A1 i A2,pa rješavati sustav.(samo mala opaska  ) )
najbolje je ovako kako si počeo,ali prije toga ortonormiraj A1 i A2 
p.s.M^t mi je oznaka za ortogonalnu komplement od M
p.s.s. izgleda da su nešto krivo napisali u zadatku? piše Prikazite matricu A u obliku A = B +C, takoda je A iz M, a B iz M^t. valjda se misli B iz M, C iz M^t..ili?
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 15:39 čet, 13. 5. 2010 Naslov: Postano: 15:39 čet, 13. 5. 2010 Naslov: |
    |
|
|
neeee... tj.da,al nemoj si zagorčavat život.. :D
prvo ortonormiraj pomoću gram-schmidta A1 i A2,nazovimo tu novu ortonormiranu bazu sa A1˘ i A2ˇ - to je i dalje baza za M. znači da je B i dalje prikaziv pomoću njih -> B= aA1ˇ + bA2ˇ. sada,budući da je {A1˘, A2ˇ} ortonormirana baza, a=<B,A1ˇ>, b=<B,A2ˇ>. sada je C=A-B. i to je to.
ovako kako si napisao,imao stvaaarno previše računanja,a nije potrebno!
hm,sad baš gledam,kako si mislio riješiti ovo? da nebi bilo da sam ti rekla da je taj način dobar,a ustvari nije..
neeee... tj.da,al nemoj si zagorčavat život.. 
prvo ortonormiraj pomoću gram-schmidta A1 i A2,nazovimo tu novu ortonormiranu bazu sa A1˘ i A2ˇ - to je i dalje baza za M. znači da je B i dalje prikaziv pomoću njih -> B= aA1ˇ + bA2ˇ. sada,budući da je {A1˘, A2ˇ} ortonormirana baza, a=<B,A1ˇ>, b=<B,A2ˇ>. sada je C=A-B. i to je to.
ovako kako si napisao,imao stvaaarno previše računanja,a nije potrebno!
hm,sad baš gledam,kako si mislio riješiti ovo? da nebi bilo da sam ti rekla da je taj način dobar,a ustvari nije..
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:48 pet, 14. 5. 2010 Naslov: Postano: 20:48 pet, 14. 5. 2010 Naslov: |
    |
|
|
Dobi se [latex]q(t) = 2 - 3 t - 2 t^2[/latex] i [latex]r(t) = -7 - 8 t + 5 t^2[/latex]. Prvo sam ortonormirao bazu za L [latex]\{p_1, p_2\}[/latex] i dobio ONB [latex]\{e_1, e_2\}[/latex], gdje je [latex]e_1(t) = \sqrt{\frac{3}{14}} (1 - 2 t)[/latex] i [latex]e_2(t) = \frac{1}{7} \sqrt{\frac{35}{26}} (4 - t - 14 t^2)[/latex]. Tada je [latex]q(t) = \langle p, e_1\rangle e_1 + \langle p, e_2\rangle e_2[/latex] ([latex]\langle p, e_1\rangle = \frac{20}{3} \sqrt{\frac{3}{14}}[/latex], [latex]\langle p, e_2\rangle = \sqrt{\frac{26}{35}}[/latex]) i [latex]r(t) = p(t) - q(t)[/latex].
Dobi se  i i 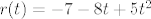 . Prvo sam ortonormirao bazu za L . Prvo sam ortonormirao bazu za L 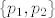 i dobio ONB i dobio ONB 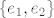 , gdje je , gdje je 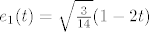 i i 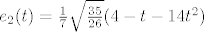 . Tada je . Tada je 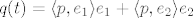 ( (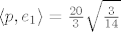 , , 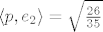 ) i ) i 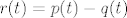 . .
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 17:19 uto, 18. 5. 2010 Naslov: Postano: 17:19 uto, 18. 5. 2010 Naslov: |
    |
|
|
Za ovo drugo, mogu se ubacit bilokoja 2 vektora tako da skup bude nezavisan (tocnije: baza) , pa se ortonormira baza pomocu GS (s tim da su prva dva vektora vec ortonormirana)
Za ono prvo, u a) zadatku te traze da odredis A*. Kad imas A i A*, onda se odredi A+A*, pa znamo i njegovu matricu, koja se onda najobicnije (vise se ne smije rec normalno :D) dijagonalizira, samo sto se dobivena baza u kojoj je matrica dijagonalna onda jos mora ortonormirati. (Mozemo naci ortonormiranu bazu u kojoj je A+A* dijagonalan bas zato sto je hermitski)
Za ovo drugo, mogu se ubacit bilokoja 2 vektora tako da skup bude nezavisan (tocnije: baza) , pa se ortonormira baza pomocu GS (s tim da su prva dva vektora vec ortonormirana)
Za ono prvo, u a) zadatku te traze da odredis A*. Kad imas A i A*, onda se odredi A+A*, pa znamo i njegovu matricu, koja se onda najobicnije (vise se ne smije rec normalno  ) dijagonalizira, samo sto se dobivena baza u kojoj je matrica dijagonalna onda jos mora ortonormirati. (Mozemo naci ortonormiranu bazu u kojoj je A+A* dijagonalan bas zato sto je hermitski) ) dijagonalizira, samo sto se dobivena baza u kojoj je matrica dijagonalna onda jos mora ortonormirati. (Mozemo naci ortonormiranu bazu u kojoj je A+A* dijagonalan bas zato sto je hermitski)
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 20:28 pet, 21. 5. 2010 Naslov: Postano: 20:28 pet, 21. 5. 2010 Naslov: |
    |
|
|
Mislim da je A*(x,y,z)=(3/2x+i/2z, 3iy, i/2x+3/2z), ak nisam nes fulo
Mislim da je A*(x,y,z)=(3/2x+i/2z, 3iy, i/2x+3/2z), ak nisam nes fulo
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|



















