|
Imas zadane matrice:
[latex]S_1 = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, \quad S_2 = \begin{bmatrix} 1 & 2 \\ 0 & 0 \end{bmatrix}, \quad S_3 = \begin{bmatrix} 1 & 2 \\ 3 & 0 \end{bmatrix}[/latex].
Tebe zanimaju sve matrice
[latex]X = \begin{bmatrix} a & b \\ c & d \end{bmatrix}[/latex]
takve da je
[latex]\operatorname{tr} S_kX^\tau = 0, \quad k = 1, 2, 3[/latex].
Uvrstis i dobijes tri jednadzbe s 4 nepoznanice:
[latex]$\begin{align*}
a &= 0, \\
a + 2b &= 0, \\
a + 2b + 3c &= 0.
\end{align*}$[/latex]
Dakle, rješenje je:
[latex]X = \begin{bmatrix} 0 & 0 \\ 0 & d \end{bmatrix}, \quad d \in \mathbb{R}[/latex].
E sad, meni ovo izgleda banalno... ali ne vidim gdje sam fulao (a ne da mi se traziti :oops:), no princip je tu.
Usput, svejedno je gledas li [latex]\operatorname{tr} S_kX^\tau = 0[/latex] ili [latex]\operatorname{tr} XS_k^\tau = 0[/latex] jer je [latex]\operatorname{tr} A = \operatorname{tr} A^\tau[/latex], pa imas:
[latex]\operatorname{tr} S_kX^\tau = \operatorname{tr} (S_kX^\tau)^\tau = \operatorname{tr} XS_k^\tau[/latex].
Naravno, da to ne vrijedi, ne bi imao skalarni produkt.
Imas zadane matrice:
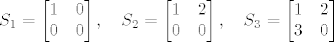 . .
Tebe zanimaju sve matrice
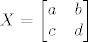
takve da je
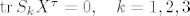 . .
Uvrstis i dobijes tri jednadzbe s 4 nepoznanice:
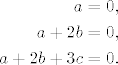
Dakle, rješenje je:
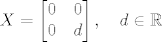 . .
E sad, meni ovo izgleda banalno... ali ne vidim gdje sam fulao (a ne da mi se traziti  ), no princip je tu. ), no princip je tu.
Usput, svejedno je gledas li 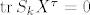 ili ili 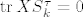 jer je jer je 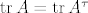 , pa imas: , pa imas:
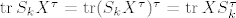 . .
Naravno, da to ne vrijedi, ne bi imao skalarni produkt.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |





