Uvrsti što imaš...
[latex]4 \cdot 10^{11} \cdot 5^2 = 10^{-11} \cdot r_{12}^2 \\
4 \cdot 10^{11} \cdot r_{23}^2 = 10^{-11} \cdot r_{12}^2 \\
4 \cdot 10^{11} \cdot r_{23}^2 = 10^{-11} \cdot r_{12}^2[/latex]
Zadnje dvije jednadžbe su identične, pa možemo pisati samo
[latex]4 \cdot 10^{11} \cdot 5^2 = 10^{-11} \cdot r_{12}^2 \\
4 \cdot 10^{11} \cdot r_{23}^2 = 10^{-11} \cdot r_{12}^2[/latex]
Odnosno
[latex]10^{13} = 10^{-11} \cdot r_{12}^2 \\
4 \cdot 10^{11} \cdot r_{23}^2 = 10^{-11} \cdot r_{12}^2[/latex]
Iz prve jednadžbe direktno dobijemo
[latex]r_{12}^2 = 10^{24} \implies r_{12} = \pm 10^{12}[/latex]
Hm, to je to... Tražilo se [latex]r_{13}[/latex] i [latex]r_{12}[/latex]...ovaj prvi je već bio zadan, a drugi je sada izračunat.
EDIT: jesi siguran da ovaj sustav, odnosno uvjeti, štimaju? :D Izračunaj [latex]r_{23}[/latex], a onda pogledaj ovaj uvjet koji povezuje [latex]r_{12}, r_{23}, r_{13}[/latex]
Uvrsti što imaš...
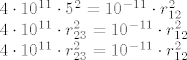
Zadnje dvije jednadžbe su identične, pa možemo pisati samo
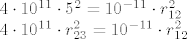
Odnosno
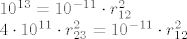
Iz prve jednadžbe direktno dobijemo

Hm, to je to... Tražilo se 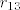 i
i 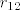 ...ovaj prvi je već bio zadan, a drugi je sada izračunat.
...ovaj prvi je već bio zadan, a drugi je sada izračunat.
EDIT: jesi siguran da ovaj sustav, odnosno uvjeti, štimaju?  Izračunaj
Izračunaj 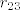 , a onda pogledaj ovaj uvjet koji povezuje
, a onda pogledaj ovaj uvjet koji povezuje 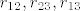
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein





