|
Vjerojatno misliš na zatvarač grafa funkcije [latex]f : \langle 0, +\infty \rangle \to \mathbb{R}[/latex], [latex]f(x) = \sin \frac{1}{x}[/latex]. Nekako je očito [latex]\overline{\Gamma_f} = \Gamma_f \cup (\{0\} \times [-1, 1])[/latex]. Vidimo su skupovi [latex]\Gamma_f[/latex] i [latex]\{0\} \times [-1, 1][/latex] svaki za sebe povezani i povezani putevima [size=7](lako se pokaže da su povezani putevima, a to implicira da su i povezani)[/size].
Pitanje je što je s njihovom unijom. Argument (laički) za povezanost ta dva skupa je što su "preblizu" [size=7](njihova udaljenost je doista jednaka 0)[/size] da bi mogli naći dva otvorena skupa takva da je prvi nadskup od [latex]\{0\} \times [-1, 1][/latex], a drugi od [latex]\Gamma_f[/latex] [size=7](može se formalno dokazati da svaki otvoreni nadskup od {0}x[-1,1] sadržava barem jednu točku iz grafa fje f)[/size]. Za povezanost putevima je protuargument (opet laički) to što su ipak ta dva skupa "odvojena" [size=7](formalni argument za nepostojanje [b]neprekidne[/b] funkcije a : [0, 1] -> {zatvarač grafa} td. je, npr. a(0) = (0, 0) i a(1) = (1/pi, 0) je taj što je limes zdesna funkcije f u 0 ne postoji, pa fja a ne može biti neprekidna)[/size].
Nisam se mogao zadržati na laičkom. :)
Vjerojatno misliš na zatvarač grafa funkcije 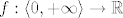 , , 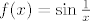 . Nekako je očito . Nekako je očito 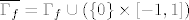 . Vidimo su skupovi . Vidimo su skupovi 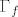 i i 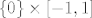 svaki za sebe povezani i povezani putevima (lako se pokaže da su povezani putevima, a to implicira da su i povezani). svaki za sebe povezani i povezani putevima (lako se pokaže da su povezani putevima, a to implicira da su i povezani).
Pitanje je što je s njihovom unijom. Argument (laički) za povezanost ta dva skupa je što su "preblizu" (njihova udaljenost je doista jednaka 0) da bi mogli naći dva otvorena skupa takva da je prvi nadskup od 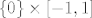 , a drugi od , a drugi od 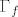 (može se formalno dokazati da svaki otvoreni nadskup od {0}x[-1,1] sadržava barem jednu točku iz grafa fje f). Za povezanost putevima je protuargument (opet laički) to što su ipak ta dva skupa "odvojena" (formalni argument za nepostojanje neprekidne funkcije a : [0, 1] → {zatvarač grafa} td. je, npr. a(0) = (0, 0) i a(1) = (1/pi, 0) je taj što je limes zdesna funkcije f u 0 ne postoji, pa fja a ne može biti neprekidna). (može se formalno dokazati da svaki otvoreni nadskup od {0}x[-1,1] sadržava barem jednu točku iz grafa fje f). Za povezanost putevima je protuargument (opet laički) to što su ipak ta dva skupa "odvojena" (formalni argument za nepostojanje neprekidne funkcije a : [0, 1] → {zatvarač grafa} td. je, npr. a(0) = (0, 0) i a(1) = (1/pi, 0) je taj što je limes zdesna funkcije f u 0 ne postoji, pa fja a ne može biti neprekidna).
Nisam se mogao zadržati na laičkom. 
|





