| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)
Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 17:52 sub, 5. 2. 2005 Naslov: |
    |
|
|
[quote="HijenA"]znam da se matrica moze dijagonalizirati ako su joj algebarske kratnosti jednake geometrijskim kratnostima[/quote]
To je samo kriterij kada se može dijagonalizirati, a nije postupak kako se to radi.
Treba naći po jednu bazu svakog svojstvenog potprostora. Unija svih tih baza čini bazu cijelog prostora u kojoj se operator (matrica) dijagonalizira. Matrica P koja se traži u zadatku je matrica prijelaza iz kanonske baze u traženu (dijagonalizirajuću) bazu. Nju ćemo dobiti tako da po stupcima napišemo vektore dobivene (dijagonalizirajuće) baze u kanonskoj bazi.
Katakteristični polinom je [latex]-(\lambda+1)\lambda(\lambda-1)[/latex] pa su svojstvene vrijednosti -1,0,1.
Svojstveni potprostori su (kratki račun - rješavanje sustava):
Ker (A+I) = [{(2,-1,1)}]
Ker A = [{(1,-1,1)}]
Ker (A-I) = [{(-1,-2,1)}]
Zato je P=
[code:1] 2 1 -1
-1 -1 -2
1 1 1[/code:1]
| HijenA (napisa): | | znam da se matrica moze dijagonalizirati ako su joj algebarske kratnosti jednake geometrijskim kratnostima |
To je samo kriterij kada se može dijagonalizirati, a nije postupak kako se to radi.
Treba naći po jednu bazu svakog svojstvenog potprostora. Unija svih tih baza čini bazu cijelog prostora u kojoj se operator (matrica) dijagonalizira. Matrica P koja se traži u zadatku je matrica prijelaza iz kanonske baze u traženu (dijagonalizirajuću) bazu. Nju ćemo dobiti tako da po stupcima napišemo vektore dobivene (dijagonalizirajuće) baze u kanonskoj bazi.
Katakteristični polinom je 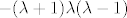 pa su svojstvene vrijednosti -1,0,1.
Svojstveni potprostori su (kratki račun - rješavanje sustava):
Ker (A+I) = [{(2,-1,1)}]
Ker A = [{(1,-1,1)}]
Ker (A-I) = [{(-1,-2,1)}]
Zato je P=
| Kod: | 2 1 -1
-1 -1 -2
1 1 1 |
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)
Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol:
Lokacija: Prazan skup ;-)
|
| Postano: 17:58 sub, 5. 2. 2005 Naslov: |
|
|
|
[quote="vjekovac"][quote="HijenA"]znam da se matrica moze dijagonalizirati ako su joj algebarske kratnosti jednake geometrijskim kratnostima[/quote]
To je samo kriterij kada se može dijagonalizirati, a nije postupak kako se to radi.
Treba naći po jednu bazu svakog svojstvenog potprostora. Unija svih tih baza čini bazu cijelog prostora u kojoj se operator (matrica) dijagonalizira. Matrica P koja se traži u zadatku je matrica prijelaza iz kanonske baze u traženu (dijagonalizirajuću) bazu. Nju ćemo dobiti tako da po stupcima napišemo vektore dobivene (dijagonalizirajuće) baze u kanonskoj bazi.[/quote]
i mislio sam da se mora racunati karakteristicni polinom ali nisam bio siguran da li to radi kad je u pitanju matrica a ne lin. operator.
[quote]
Katakteristični polinom je [latex]-(\lambda+1)\lambda(\lambda-1)[/latex] pa su svojstvene vrijednosti -1,0,1.
Svojstveni potprostori su (kratki račun - rješavanje sustava):
Ker (A+I) = [{(2,-1,1)}]
Ker A = [{(1,-1,1)}]
Ker (A-I) = [{(-1,-2,1)}][/quote]
ti si tu uvrstio umjesto [latex]\lambda[/latex] svojstvenu vrijednost, odnosno sve 3 svojstvene vrijednosti?
| vjekovac (napisa): | | HijenA (napisa): | | znam da se matrica moze dijagonalizirati ako su joj algebarske kratnosti jednake geometrijskim kratnostima |
To je samo kriterij kada se može dijagonalizirati, a nije postupak kako se to radi.
Treba naći po jednu bazu svakog svojstvenog potprostora. Unija svih tih baza čini bazu cijelog prostora u kojoj se operator (matrica) dijagonalizira. Matrica P koja se traži u zadatku je matrica prijelaza iz kanonske baze u traženu (dijagonalizirajuću) bazu. Nju ćemo dobiti tako da po stupcima napišemo vektore dobivene (dijagonalizirajuće) baze u kanonskoj bazi. |
i mislio sam da se mora racunati karakteristicni polinom ali nisam bio siguran da li to radi kad je u pitanju matrica a ne lin. operator.
| Citat: |
Katakteristični polinom je 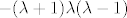pa su svojstvene vrijednosti -1,0,1.
Svojstveni potprostori su (kratki račun - rješavanje sustava):
Ker (A+I) = [{(2,-1,1)}]
Ker A = [{(1,-1,1)}]
Ker (A-I) = [{(-1,-2,1)}] |
ti si tu uvrstio umjesto  svojstvenu vrijednost, odnosno sve 3 svojstvene vrijednosti?
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 18:05 sub, 5. 2. 2005 Naslov: |
|
|
|
[quote="HijenA"]i mislio sam da se mora racunati karakteristicni polinom ali nisam bio siguran da li to radi kad je u pitanju matrica a ne lin. operator.[/quote]
Pa karakteristični polinom se izvorno i definira za matricu. To što dvije slične matrice imaju isti karakteristični polinom, pa možemo govoriti o karakterističnom polinomu operatora, je drugi par čarapa. :-)
[quote][quote]Svojstveni potprostori su (kratki račun - rješavanje sustava):
Ker (A+I) = [{(2,-1,1)}]
Ker A = [{(1,-1,1)}]
Ker (A-I) = [{(-1,-2,1)}][/quote]
ti si tu uvrstio umjesto [latex]\lambda[/latex] svojstvenu vrijednost, odnosno sve 3 svojstvene vrijednosti?[/quote]
Upravo tako. Svojstveni potprostor od lam je skup svih x takvih da je Ax=lamx , odnosno (A-lam*I)x=0 -- dakle to je jezgra od A-lam*I . Na primjer, svojstveni potprostor od -1 je zapravo jezgra od A+I .
HTH,
| HijenA (napisa): | | i mislio sam da se mora racunati karakteristicni polinom ali nisam bio siguran da li to radi kad je u pitanju matrica a ne lin. operator. |
Pa karakteristični polinom se izvorno i definira za matricu. To što dvije slične matrice imaju isti karakteristični polinom, pa možemo govoriti o karakterističnom polinomu operatora, je drugi par čarapa. 
| Citat: | | Citat: | Svojstveni potprostori su (kratki račun - rješavanje sustava):
Ker (A+I) = [{(2,-1,1)}]
Ker A = [{(1,-1,1)}]
Ker (A-I) = [{(-1,-2,1)}] |
ti si tu uvrstio umjesto svojstvenu vrijednost, odnosno sve 3 svojstvene vrijednosti? |
Upravo tako. Svojstveni potprostor od lam je skup svih x takvih da je Ax=lamx , odnosno (A-lam*I)x=0 – dakle to je jezgra od A-lam*I . Na primjer, svojstveni potprostor od -1 je zapravo jezgra od A+I .
HTH,
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol:
|
| Postano: 18:06 sub, 5. 2. 2005 Naslov: |
|
|
|
[quote="HijenA"]i mislio sam da se mora racunati karakteristicni polinom[/quote]
Pa karakteristični polinom mi je trebao da nađem spektar. Obično se tako krene.
[quote="HijenA"]ali nisam bio siguran da li to radi kad je u pitanju matrica a ne lin. operator.[/quote]
:?
Jedna od osnovnih poanti Linerane algebre je da (uz fiksiranu bazu) postoji korespondencija (preciznije izomorfizam algebri, ali nema veze) između linearnih operatora i matrica.
Ako imaš danu matricu, onda je uvijek shvatiš kao matricu nekog linearnog operatora u kanonskoj bazi. (Tada za matrice imaju smisla svi pojmovi kao i za linearne operatore.)
[quote="HijenA"]
ti si tu uvrstio umjesto [latex]\lambda[/latex] svojstvenu vrijednost, odnosno sve 3 svojstvene vrijednosti?[/quote]
Da. Svojstveni potprostori pridruženi sv. vrij. -1,0,1 su redom
Ker (A-(-1)I) = Ker (A+I)
Ker (A-0I) = Ker A
Ker (A-1I) = Ker (A-I)
| HijenA (napisa): | | i mislio sam da se mora racunati karakteristicni polinom |
Pa karakteristični polinom mi je trebao da nađem spektar. Obično se tako krene.
| HijenA (napisa): | | ali nisam bio siguran da li to radi kad je u pitanju matrica a ne lin. operator. |
Jedna od osnovnih poanti Linerane algebre je da (uz fiksiranu bazu) postoji korespondencija (preciznije izomorfizam algebri, ali nema veze) između linearnih operatora i matrica.
Ako imaš danu matricu, onda je uvijek shvatiš kao matricu nekog linearnog operatora u kanonskoj bazi. (Tada za matrice imaju smisla svi pojmovi kao i za linearne operatore.)
| HijenA (napisa): |
ti si tu uvrstio umjesto svojstvenu vrijednost, odnosno sve 3 svojstvene vrijednosti? |
Da. Svojstveni potprostori pridruženi sv. vrij. -1,0,1 su redom
Ker (A-(-1)I) = Ker (A+I)
Ker (A-0I) = Ker A
Ker (A-1I) = Ker (A-I)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)
Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol:
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)
Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol:
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
| Postano: 17:23 ned, 6. 2. 2005 Naslov: |
|
|
|
[quote="HijenA"]eto...jos jedno pitanje. meni nije jasno kak si dobio sljedecu stvar
Ker (A-I)=[{(-1,-2,1)}]
naime...imam sljedecu stvar
[latex]A-I=\left ( \begin{array}{rlc} -3 & 5 & 7 \\ 1 & -1 & -1 \\ -1 & 1 & 1 \end{array} \right) \sim \left( \begin{array}{rlc} -3 & 5 & 7 \\ 1 & -1 & -1 \\ 0 & 0 & 0 \end{array} \right) \sim \left( \begin{array}{rlc} 0 & 2 & 4 \\ 1 & -1 & -1 \\ 0 & 0 & 0 \end{array} \right)[/latex]
[/quote]
prvi redak podijeli sa 2, i onda ga dodaj drugom retku! dobijes
0 1 2
1 0 1
0 0 0
tj. x1=-x3, x2=-2x3, kuzis?
| HijenA (napisa): | eto...jos jedno pitanje. meni nije jasno kak si dobio sljedecu stvar
Ker (A-I)=[{(-1,-2,1)}]
naime...imam sljedecu stvar
|
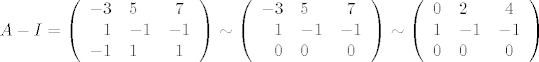
prvi redak podijeli sa 2, i onda ga dodaj drugom retku! dobijes
0 1 2
1 0 1
0 0 0
tj. x1=-x3, x2=-2x3, kuzis?
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
HijenA
Forumaš(ica)
Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol:
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
gdje sam fulao?! 
