| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 17:22 ned, 17. 10. 2010 Naslov: Postano: 17:22 ned, 17. 10. 2010 Naslov: |
    |
|
|
Nisam siguran jesam li skužio pitanje, [latex]\left[ \begin{array}{lrc} 1 & 1 \\ 1 & 1 \end{array} \right][/latex] i [latex]\left[ \begin{array}{lrc} 1 & 1 \\ 1 & 2 \end{array} \right][/latex] su dvije matrice iz [latex]M_2(\mathbb{R})[/latex]. Možeš ih označavati bilo uglatim bilo oblim zagradama, svejedno je.
Dakle, te dvije matrice su dva vektora u ovom četverodimenzionalnom vektorskom prostoru, i sad trebaš naći još dvije koje će zajedno s ovima činiti bazu, kao i inače u takvim zadacima. Znaš sada, ili treba rješenje?
Nisam siguran jesam li skužio pitanje, 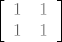 i i 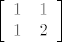 su dvije matrice iz su dvije matrice iz 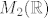 . Možeš ih označavati bilo uglatim bilo oblim zagradama, svejedno je. . Možeš ih označavati bilo uglatim bilo oblim zagradama, svejedno je.
Dakle, te dvije matrice su dva vektora u ovom četverodimenzionalnom vektorskom prostoru, i sad trebaš naći još dvije koje će zajedno s ovima činiti bazu, kao i inače u takvim zadacima. Znaš sada, ili treba rješenje?
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
lavicha
Forumaš(ica)
Pridružen/a: 15. 10. 2010. (18:25:49)
Postovi: (1A)16
|
 Postano: 20:54 ned, 17. 10. 2010 Naslov: Postano: 20:54 ned, 17. 10. 2010 Naslov: |
    |
|
|
Dodaj kanonsku bazu (e1,e2,e3,e4) i tada prikazuj pomocu predhodnika svaki dok ne dobijes bazu M2(R).. rjesenje je na kraju (a1,a2,e1,e2).
ako ti treba detaljniji postupak, samo reci :)
Dodaj kanonsku bazu (e1,e2,e3,e4) i tada prikazuj pomocu predhodnika svaki dok ne dobijes bazu M2(R).. rjesenje je na kraju (a1,a2,e1,e2).
ako ti treba detaljniji postupak, samo reci 
_________________ ....I think about the little things that make life great!!  |
|
| [Vrh] |
|
Optik
Forumaš(ica)

Pridružen/a: 12. 07. 2010. (01:11:37)
Postovi: (2)16
|
|
| [Vrh] |
|
lavicha
Forumaš(ica)
Pridružen/a: 15. 10. 2010. (18:25:49)
Postovi: (1A)16
|
 Postano: 21:22 ned, 17. 10. 2010 Naslov: Postano: 21:22 ned, 17. 10. 2010 Naslov: |
    |
|
|
dakle isprobavas koji se daju prikazati kao linearna kombinacija pomocu predhodnika..a to radis kako bi dobio linearno nezavisni skup,koji je tada baza. vidis da a2,e1,e2 ne idu kao linearne kombinacije,ali e3=2a1-a2-e1-e2, pa se izbacuje e3, i onda dobijes e4=-a1+a2, pa izbacis e4. nakon toga ostane baza (a1,a2,e1,e2) i to je to..
dakle isprobavas koji se daju prikazati kao linearna kombinacija pomocu predhodnika..a to radis kako bi dobio linearno nezavisni skup,koji je tada baza. vidis da a2,e1,e2 ne idu kao linearne kombinacije,ali e3=2a1-a2-e1-e2, pa se izbacuje e3, i onda dobijes e4=-a1+a2, pa izbacis e4. nakon toga ostane baza (a1,a2,e1,e2) i to je to..
_________________ ....I think about the little things that make life great!!  |
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 20:24 pon, 18. 10. 2010 Naslov: Postano: 20:24 pon, 18. 10. 2010 Naslov: |
    |
|
|
hvala svima ,samo nisam skuzio da se to moze zapisat(mislim moze...,nemoze al je ista stvar ko i) u obliku normalnih zagrada ( 1,1,1,1) pa je zadatak ustvari jednostavan...
hvala svima ,samo nisam skuzio da se to moze zapisat(mislim moze...,nemoze al je ista stvar ko i) u obliku normalnih zagrada ( 1,1,1,1) pa je zadatak ustvari jednostavan...
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
|







