| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
chiko
Forumaš(ica)


Pridružen/a: 14. 09. 2010. (17:43:27)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 16:32 uto, 19. 10. 2010 Naslov: Postano: 16:32 uto, 19. 10. 2010 Naslov: |
    |
|
|
Vjerojatno je to negdje odgovoreno na forumu, ali dovoljno sam lijen da sad ne tražim. :) Uglavnom, ideja je iskoristiti da je [latex]g[/latex] zapravo u potpunosti definiran s vrijednostima [latex]f(a)[/latex], gdje su [latex]a[/latex] proizvoljni pozitivni brojevi. Drugim riječima, kako je [latex]3^x+9^x>0[/latex], nas zapravo ne zanimaju vrijednosti funkcije [latex]f[/latex] u negativnim brojevima.
Stoga, želimo pronaći funkciju [latex]f[/latex] koja je surjektivna na [latex]\langle 0,+\infty\rangle[/latex] (a za ostatak nam je svejedno kako je definirana). Pa dobro, definirajmo [latex]f[/latex] ovako: [latex]f(x)=0[/latex] za [latex]x\leq 0[/latex] i [latex]f(x)=\ln x[/latex] za [latex]x>0[/latex].
Funkcija [latex]f[/latex] je očito dobro definirana, a i jasno je da je surjekcija (već se za pozitivne [latex]x[/latex] postižu svi realni brojevi jer je [latex]\ln[/latex] surjekcija). [latex]g[/latex] je zapravo definirana s [latex]\ln (9^x+3^x)[/latex], pa vrijedi da je i injekcija (jer su i [latex]\ln[/latex] i [latex]9^x+3^x[/latex] injekcije), a i surjekcija. Naime, za [latex]9^x+3^x[/latex] postižu se sve pozitivne vrijednosti, a [latex]\ln[/latex] je surjektivna na upravo toj domeni. Može se to i raspisati malo preciznije preko slike kompozicije, ali stvar je ista. :)
Evo, mislim da bi to moglo biti OK. Uglavnom, zapravo nam je jedina ideja bila pronaći funkciju koja je surjektivna na [latex]\langle 0,+\infty\rangle[/latex].
Vjerojatno je to negdje odgovoreno na forumu, ali dovoljno sam lijen da sad ne tražim.  Uglavnom, ideja je iskoristiti da je Uglavnom, ideja je iskoristiti da je  zapravo u potpunosti definiran s vrijednostima zapravo u potpunosti definiran s vrijednostima 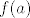 , gdje su , gdje su  proizvoljni pozitivni brojevi. Drugim riječima, kako je proizvoljni pozitivni brojevi. Drugim riječima, kako je 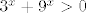 , nas zapravo ne zanimaju vrijednosti funkcije , nas zapravo ne zanimaju vrijednosti funkcije  u negativnim brojevima. u negativnim brojevima.
Stoga, želimo pronaći funkciju  koja je surjektivna na koja je surjektivna na 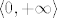 (a za ostatak nam je svejedno kako je definirana). Pa dobro, definirajmo (a za ostatak nam je svejedno kako je definirana). Pa dobro, definirajmo  ovako: ovako: 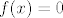 za za  i i 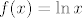 za za 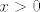 . .
Funkcija  je očito dobro definirana, a i jasno je da je surjekcija (već se za pozitivne je očito dobro definirana, a i jasno je da je surjekcija (već se za pozitivne  postižu svi realni brojevi jer je postižu svi realni brojevi jer je 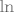 surjekcija). surjekcija).  je zapravo definirana s je zapravo definirana s 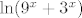 , pa vrijedi da je i injekcija (jer su i , pa vrijedi da je i injekcija (jer su i 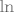 i i 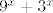 injekcije), a i surjekcija. Naime, za injekcije), a i surjekcija. Naime, za 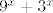 postižu se sve pozitivne vrijednosti, a postižu se sve pozitivne vrijednosti, a 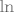 je surjektivna na upravo toj domeni. Može se to i raspisati malo preciznije preko slike kompozicije, ali stvar je ista. je surjektivna na upravo toj domeni. Može se to i raspisati malo preciznije preko slike kompozicije, ali stvar je ista. 
Evo, mislim da bi to moglo biti OK. Uglavnom, zapravo nam je jedina ideja bila pronaći funkciju koja je surjektivna na 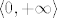 . .
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:29 pet, 22. 10. 2010 Naslov: Postano: 19:29 pet, 22. 10. 2010 Naslov: |
    |
|
|
Možeš malo precizirati kakva se pomoć traži? :) Mislim, zadatak je sam po sebi dosta straightforward, možeš i ići tražiti prasliku kompozicije, a možeš i direktnije (što je opet, zapravo, implicitno kompozicijom). Imaš, dakle, [latex]0<e^{\sin\sqrt{x}}<1[/latex]. Lijeva nejednakost uvijek vrijedi, a za desnu je logaritmiranjem dosta očito da te zanimaju iksevi takvi da je [latex]\sin\sqrt{x}<0[/latex]. To, pak, ne bi trebao biti neki problem (zapis rješenja je malo ružan, ali je legalan nonetheless :))... ili? :)
Možeš malo precizirati kakva se pomoć traži?  Mislim, zadatak je sam po sebi dosta straightforward, možeš i ići tražiti prasliku kompozicije, a možeš i direktnije (što je opet, zapravo, implicitno kompozicijom). Imaš, dakle, Mislim, zadatak je sam po sebi dosta straightforward, možeš i ići tražiti prasliku kompozicije, a možeš i direktnije (što je opet, zapravo, implicitno kompozicijom). Imaš, dakle, 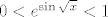 . Lijeva nejednakost uvijek vrijedi, a za desnu je logaritmiranjem dosta očito da te zanimaju iksevi takvi da je . Lijeva nejednakost uvijek vrijedi, a za desnu je logaritmiranjem dosta očito da te zanimaju iksevi takvi da je 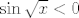 . To, pak, ne bi trebao biti neki problem (zapis rješenja je malo ružan, ali je legalan nonetheless . To, pak, ne bi trebao biti neki problem (zapis rješenja je malo ružan, ali je legalan nonetheless  )... ili? )... ili? 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:20 sub, 23. 10. 2010 Naslov: Postano: 7:20 sub, 23. 10. 2010 Naslov: |
    |
|
|
Pa to i nije neki problem, makar odvratno izgleda. :) Dakle, imamo [latex]\displaystyle\sqrt{x}\in\bigcup_{k\in\mathbb{N}_0}\langle \pi+2k\pi,2\pi+2k\pi\rangle[/latex] ([latex]k[/latex] je nužno nenegativan a ne samo cijeli jer je [latex]\sqrt{x}[/latex] veći ili jednak [latex]0[/latex]). Kvadriranjem dobivamo [latex]\displaystyle x\in\bigcup_{k\in\mathbb{N}_0}\langle \pi^2(1+2k)^2,\pi^2(2+2k)^2\rangle[/latex].
Postoji, naravno, više varijanti zapisa. Koliko vidim, WolframAlpha nudi [latex]\displaystyle\bigcup_{k\in\mathbb{N}}\langle \pi^2(2k-1)^2,\pi^2(2k)^2\rangle[/latex], što je očito isto.
Pa to i nije neki problem, makar odvratno izgleda.  Dakle, imamo Dakle, imamo 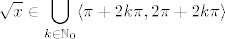 ( ( je nužno nenegativan a ne samo cijeli jer je je nužno nenegativan a ne samo cijeli jer je 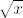 veći ili jednak veći ili jednak  ). Kvadriranjem dobivamo ). Kvadriranjem dobivamo 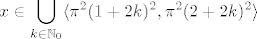 . .
Postoji, naravno, više varijanti zapisa. Koliko vidim, WolframAlpha nudi 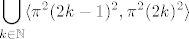 , što je očito isto. , što je očito isto.
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:06 sub, 23. 10. 2010 Naslov: Postano: 12:06 sub, 23. 10. 2010 Naslov: |
    |
|
|
Ne bih baš puno nade polagao u crtanje toga. :) Stoga ostaje čisti, direktni račun, čak nisu uočljive ni neke pametne kompozicije. Prvo, primijeti da uvijek vrijedi [latex]|2x^2+2x-|x^2-1||\geq 0[/latex]. Stoga nas zapravo samo zanima pronaći rješenja od [latex]|2x^2+2x-|x^2-1|\leq 1[/latex], odnosno od [latex]-1 \leq 2x^2+2x-|x^2-1|\leq 1[/latex].
Sad smo u biti došli do kraja bilo čega pametnog i ostaje nam samo rastaviti stvar na dva-tri slučaja i rješavati hrpu kvadratnih jednadžbi. Možda se najintuitivnije čini rastaviti stvar na [latex]x\leq -1[/latex], [latex]-1<x\leq 1[/latex] i [latex]1<x[/latex]. To činimo, naravno, kako bismo se riješili apsolutnih vrijednosti u izrazu. U prvom i trećem slučaju tako dobivamo [latex]-1\leq x^2+2x+1\leq 1[/latex], a u drugom, ako se ne varam, [latex]-1\leq 3x^2+2x-1\leq 1[/latex]. Sad samo ostaje da riješiš kvadratne jednadžbe i pronađeš intervale za koje vrijede gornje nejednadžbe, presječeš to s uvjetima svakog slučaja te na kraju uzmeš uniju rješenja ta tri slučaja.
Završno rješenje bi trebalo imati, ako se ne varam, nekakve korijene od sedam u sebi. Aha, evo, WolframAlpha [url=http://www.wolframalpha.com/input/?i=solve+-1%3C%3D2x%5E2%2B2x-abs%28x%5E2-1%29%3C%3D1]kaže[/url] da je rješenje [latex]\[-2,-\displaystyle\frac{2}{3}\]\cup\[0,\displaystyle\frac{\sqrt{7}-1}{3}\][/latex].
Ne bih baš puno nade polagao u crtanje toga.  Stoga ostaje čisti, direktni račun, čak nisu uočljive ni neke pametne kompozicije. Prvo, primijeti da uvijek vrijedi Stoga ostaje čisti, direktni račun, čak nisu uočljive ni neke pametne kompozicije. Prvo, primijeti da uvijek vrijedi 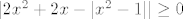 . Stoga nas zapravo samo zanima pronaći rješenja od . Stoga nas zapravo samo zanima pronaći rješenja od 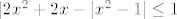 , odnosno od , odnosno od 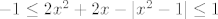 . .
Sad smo u biti došli do kraja bilo čega pametnog i ostaje nam samo rastaviti stvar na dva-tri slučaja i rješavati hrpu kvadratnih jednadžbi. Možda se najintuitivnije čini rastaviti stvar na 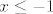 , , 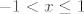 i i 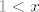 . To činimo, naravno, kako bismo se riješili apsolutnih vrijednosti u izrazu. U prvom i trećem slučaju tako dobivamo . To činimo, naravno, kako bismo se riješili apsolutnih vrijednosti u izrazu. U prvom i trećem slučaju tako dobivamo 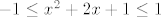 , a u drugom, ako se ne varam, , a u drugom, ako se ne varam, 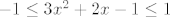 . Sad samo ostaje da riješiš kvadratne jednadžbe i pronađeš intervale za koje vrijede gornje nejednadžbe, presječeš to s uvjetima svakog slučaja te na kraju uzmeš uniju rješenja ta tri slučaja. . Sad samo ostaje da riješiš kvadratne jednadžbe i pronađeš intervale za koje vrijede gornje nejednadžbe, presječeš to s uvjetima svakog slučaja te na kraju uzmeš uniju rješenja ta tri slučaja.
Završno rješenje bi trebalo imati, ako se ne varam, nekakve korijene od sedam u sebi. Aha, evo, WolframAlpha kaže da je rješenje 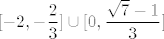 . .
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 15:47 ned, 24. 10. 2010 Naslov: Postano: 15:47 ned, 24. 10. 2010 Naslov: |
    |
|
|
[quote="Lanek_"]1. a) [latex][\sqrt{2}, \infty>[/latex]
b) [latex]x_1=0; x_2=\sqrt{1/2}; x_3=-\sqrt{1/2}[/latex]
2. [latex]f([1,3])=[0, \sqrt{1/x}][/latex]
[latex]Rf=[O,\infty> \diagdown {1}[/latex]
3.[latex]f^-1([0,1])=[-3/2, 1/2] \cup [0, 1/2][/latex]
-> ovo mi sigurno nije točno xD
4. a)[latex]f^-1=\arcsin \sqrt{y} +1[/latex]
b) to mi je ispalo da mi je konstanta al ne znam dalje kaj da radim.[/quote]
znaci 4b)
pretpostavimo da postoji padajuca funkcija.
imamo izraz f(f(x))-f(x^3)=2^f(x)
primjetimo da je ovaj prvi izraz f(f(x)) kompozicija dviju padajucih funkcija sto daje rastucu funkciju
drugi izraz f(x^3)jest padajuća funkcija po nasoj pretpostavci na pocetku zadatka ali zbog minusa postaje rastuca funkcija;
pa sveukupno na lijevoj strani imamo zbroj dviju rastucih funkcija sto je rastuca funkcija a na desnoj strani imamo padajucu funkciju,pa je nas zakljucak da ne postoji padajuca funkcija...
tako bar ja mislim da bi se moglo rjesit
| Lanek_ (napisa): | 1. a) 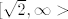
b) 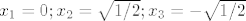
2. 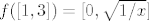
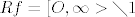
3.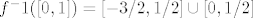
→ ovo mi sigurno nije točno xD
4. a)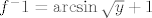
b) to mi je ispalo da mi je konstanta al ne znam dalje kaj da radim. |
znaci 4b)
pretpostavimo da postoji padajuca funkcija.
imamo izraz f(f(x))-f(x^3)=2^f(x)
primjetimo da je ovaj prvi izraz f(f(x)) kompozicija dviju padajucih funkcija sto daje rastucu funkciju
drugi izraz f(x^3)jest padajuća funkcija po nasoj pretpostavci na pocetku zadatka ali zbog minusa postaje rastuca funkcija;
pa sveukupno na lijevoj strani imamo zbroj dviju rastucih funkcija sto je rastuca funkcija a na desnoj strani imamo padajucu funkciju,pa je nas zakljucak da ne postoji padajuca funkcija...
tako bar ja mislim da bi se moglo rjesit
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
|









