|
Jest, [latex]f[/latex] je injekcija. E, sad, kako bismo to precizno zapisali:
Dakle, želimo pokazati da [latex]f[/latex] jest injekcija. Po definiciji, to znači da [latex]f(x)=f(y)\Rightarrow x=y[/latex]. Dakle, to želimo dokazati. Stoga, počinjemo s "Neka su [latex]x[/latex] i [latex]y[/latex] takvi da vrijedi [latex]f(x)=f(y)[/latex]." Želimo nekim manipulacijama doći do toga da nužno vrijedi [latex]x=y[/latex]. (Naravno, iz čiste definicije funkcije za svaki [latex]f[/latex] vrijedi i obrat, tj. [latex]x=y\Rightarrow f(x)=f(y)[/latex], ali o tome uopće ne trebamo ni razmišljati.)
Dakle, imamo [latex]f(x)=f(y)[/latex]. Sada ćemo geovati obje strane iliti primijenit ćemo [latex]g[/latex] na obje strane jednakosti. Budući da znamo da je [latex]f(x)=f(y)[/latex], nužno je i [latex]g(f(x))=g(f(y))[/latex]. Sada iskorištavamo da mi znamo koliko je [latex]g(f(x))[/latex] i [latex]g(f(y))[/latex]: imamo stoga [latex]\sinh x=\sinh y[/latex]. No, mi znamo da je sinus hiperbolni injekcija - to ste svakako rekli, a možda i dokazali. Stoga, po definiciji injekcije znamo da vrijedi [latex]\sinh x=\sinh y\Rightarrow x=y[/latex]. Kako mi znamo da je [latex]\sinh x=\sinh y[/latex], nužno, dakle, i vrijedi [latex]x=y[/latex].
Evo, sad pogledaj s čim smo počeli prethodni odlomak, a s čim završili - dobili smo upravo ono što smo htjeli: [latex]f(x)=f(y)\Rightarrow x=y[/latex]. Dakle, [latex]f[/latex] je injekcija.
Ovo je sad opisano u puno previše riječi, ali barem sam bio detaljan. :)
Jest,  je injekcija. E, sad, kako bismo to precizno zapisali: je injekcija. E, sad, kako bismo to precizno zapisali:
Dakle, želimo pokazati da  jest injekcija. Po definiciji, to znači da jest injekcija. Po definiciji, to znači da 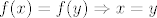 . Dakle, to želimo dokazati. Stoga, počinjemo s "Neka su . Dakle, to želimo dokazati. Stoga, počinjemo s "Neka su  i i  takvi da vrijedi takvi da vrijedi 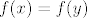 ." Želimo nekim manipulacijama doći do toga da nužno vrijedi ." Želimo nekim manipulacijama doći do toga da nužno vrijedi 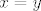 . (Naravno, iz čiste definicije funkcije za svaki . (Naravno, iz čiste definicije funkcije za svaki  vrijedi i obrat, tj. vrijedi i obrat, tj. 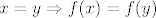 , ali o tome uopće ne trebamo ni razmišljati.) , ali o tome uopće ne trebamo ni razmišljati.)
Dakle, imamo 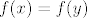 . Sada ćemo geovati obje strane iliti primijenit ćemo . Sada ćemo geovati obje strane iliti primijenit ćemo  na obje strane jednakosti. Budući da znamo da je na obje strane jednakosti. Budući da znamo da je 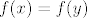 , nužno je i , nužno je i 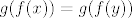 . Sada iskorištavamo da mi znamo koliko je . Sada iskorištavamo da mi znamo koliko je 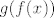 i i 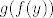 : imamo stoga : imamo stoga 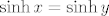 . No, mi znamo da je sinus hiperbolni injekcija - to ste svakako rekli, a možda i dokazali. Stoga, po definiciji injekcije znamo da vrijedi . No, mi znamo da je sinus hiperbolni injekcija - to ste svakako rekli, a možda i dokazali. Stoga, po definiciji injekcije znamo da vrijedi 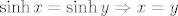 . Kako mi znamo da je . Kako mi znamo da je 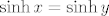 , nužno, dakle, i vrijedi , nužno, dakle, i vrijedi 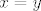 . .
Evo, sad pogledaj s čim smo počeli prethodni odlomak, a s čim završili - dobili smo upravo ono što smo htjeli: 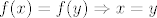 . Dakle, . Dakle,  je injekcija. je injekcija.
Ovo je sad opisano u puno previše riječi, ali barem sam bio detaljan. 
|




