| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
123456
Forumaš(ica)

Pridružen/a: 23. 10. 2010. (13:17:05)
Postovi: (6)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:34 sub, 23. 10. 2010 Naslov: Postano: 13:34 sub, 23. 10. 2010 Naslov: |
    |
|
|
Može. :) Reci, gdje su problemi? Ovako, generalno, evo za prvu ruku neki hintovi, nema smisla da rješavam cijeli zadatak ako si ti sam došao/došla recimo skoro do kraja:
1. Jedini problem koji imaš tu je da nazvnik ne smije biti 0, a area kotangens hiperbolni ima domenu [latex]\langle -\infty,-1\rangle\cup\langle 1,+\infty\rangle[/latex], pa ne smiješ imati [latex]-1\leq\displaystyle\frac{1+x}{2-x}\leq 1[/latex], a to je relativno lako riješiti.
2. Tu pronađi prvo domenu funkcije (dakle, isti zadatak kao u 1., samo nešto lakši), a nakon toga primijeti da je [latex]f=f_1\circ f_2\circ f_3\circ f_4\circ f_5[/latex], gdje je [latex]f_1(x)=x-1[/latex], [latex]f_2(x)=\sinh x[/latex], [latex]f_3(x)=5x-1[/latex], [latex]f_4(x)=\displaystyle\frac{1}{x}[/latex], [latex]f_5(x)=2+x[/latex] (valjda se nisam negdje napamet zeznuo). Dalje onda samo ideš po formuli za sliku kompozicije.
3. Možeš ići direktnije (bez kompozicija), tj. tražiti kad je [latex]1\leq \sqrt{\pi^{\cos x}}\leq 2[/latex], što ne bi trebalo biti preteško (mislim da relativno brzo ispadne da je to ekvivalentno s [latex]\cos x\geq 0[/latex]), a možeš i eksplicitno kompozicijama: uzmi [latex]f_1(x)=\sqrt{x}[/latex], [latex]f_2(x)=\pi^x[/latex] i [latex]f_3(x)=\cos x[/latex] i primijeti da je [latex]f=f_1\circ f_2\circ f_3[/latex]. Dalje onda ideš po formuli za prasliku kompozicije.
Može.  Reci, gdje su problemi? Ovako, generalno, evo za prvu ruku neki hintovi, nema smisla da rješavam cijeli zadatak ako si ti sam došao/došla recimo skoro do kraja: Reci, gdje su problemi? Ovako, generalno, evo za prvu ruku neki hintovi, nema smisla da rješavam cijeli zadatak ako si ti sam došao/došla recimo skoro do kraja:
1. Jedini problem koji imaš tu je da nazvnik ne smije biti 0, a area kotangens hiperbolni ima domenu 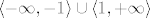 , pa ne smiješ imati , pa ne smiješ imati 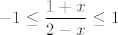 , a to je relativno lako riješiti. , a to je relativno lako riješiti.
2. Tu pronađi prvo domenu funkcije (dakle, isti zadatak kao u 1., samo nešto lakši), a nakon toga primijeti da je 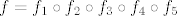 , gdje je , gdje je 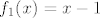 , , 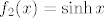 , , 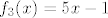 , , 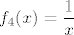 , , 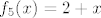 (valjda se nisam negdje napamet zeznuo). Dalje onda samo ideš po formuli za sliku kompozicije. (valjda se nisam negdje napamet zeznuo). Dalje onda samo ideš po formuli za sliku kompozicije.
3. Možeš ići direktnije (bez kompozicija), tj. tražiti kad je 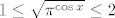 , što ne bi trebalo biti preteško (mislim da relativno brzo ispadne da je to ekvivalentno s , što ne bi trebalo biti preteško (mislim da relativno brzo ispadne da je to ekvivalentno s 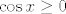 ), a možeš i eksplicitno kompozicijama: uzmi ), a možeš i eksplicitno kompozicijama: uzmi 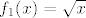 , , 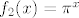 i i 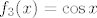 i primijeti da je i primijeti da je 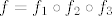 . Dalje onda ideš po formuli za prasliku kompozicije. . Dalje onda ideš po formuli za prasliku kompozicije.
|
|
| [Vrh] |
|
123456
Forumaš(ica)

Pridružen/a: 23. 10. 2010. (13:17:05)
Postovi: (6)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 16:15 sub, 23. 10. 2010 Naslov: Postano: 16:15 sub, 23. 10. 2010 Naslov: |
    |
|
|
f(x)=(1-3^x)/(2+3^x)
odredi sliku
odredi f(<-besk.,0))
muci me to sa beskonacno...kak se to inace provijerava...mislim da bi rjesenje trebalo biti (0,1/2) al do toga sam dosao preko digitrona,koji nesmijemo iamti na kolokviju,pa ako mi ko moze reci kak se to inace racuna kad imamo beskonacno jer nemogu uvrstiti neki broj...
fala
i samo mi recite i sliku da usput provijerim jel mi dobro
f(x)=(1-3^x)/(2+3^x)
odredi sliku
odredi f(<-besk.,0))
muci me to sa beskonacno...kak se to inace provijerava...mislim da bi rjesenje trebalo biti (0,1/2) al do toga sam dosao preko digitrona,koji nesmijemo iamti na kolokviju,pa ako mi ko moze reci kak se to inace racuna kad imamo beskonacno jer nemogu uvrstiti neki broj...
fala
i samo mi recite i sliku da usput provijerim jel mi dobro
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 16:30 sub, 23. 10. 2010 Naslov: Postano: 16:30 sub, 23. 10. 2010 Naslov: |
    |
|
|
[quote="123456"]zanima me samo kak u 1. zadatku odredis domenu od arcth... i mislim da ti to nije kotangens vec tangens[/quote]
* Domena od arctg je cijeli [latex]R[/latex], a domena od Arcth je <-besko.,-1>U<1,+besko.>. I sada ovo što ti se "nalazi" u Arcth ti mora biti iz tog intervala, odnoso [latex]-1>(1-x/2-x)>1[/latex] i rješiš nejednadžbu + ovdje imaš još jedan uvijet da ti x mora biti različito od 2.
i na kraju napraviš presjek od R-a i dobivenog intervala iz nejednadžbe. Eto nadam se da ti je jasnije malo.... *
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote="Lepi91"]f(x)=(1-3^x)/(2+3^x)
odredi sliku
odredi f(<-besk.,0))
muci me to sa beskonacno...kak se to inace provijerava...mislim da bi rjesenje trebalo biti (0,1/2) al do toga sam dosao preko digitrona,koji nesmijemo iamti na kolokviju,pa ako mi ko moze reci kak se to inace racuna kad imamo beskonacno jer nemogu uvrstiti neki broj...
fala
i samo mi recite i sliku da usput provijerim jel mi dobro[/quote]
Meni ovako ispada;
Rf=<1/2,+besko.>
f(<-besk.,0>)=[0,1/2>.
A kako da ti objasnim ovo sa beskonačnoću, a da bude efikasno stvarno ne bih znala, zato to preporučam vrsnijim matematičarima od mene....al savjet, nacrtaj grafove funkcija, ovu f-ju može prikazat kao kompoziciju dviju f-ja, pa se malo zagledaj u to, pa ti moža bude jasnije. :P
| 123456 (napisa): | | zanima me samo kak u 1. zadatku odredis domenu od arcth... i mislim da ti to nije kotangens vec tangens |
* Domena od arctg je cijeli 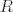 , a domena od Arcth je ←besko.,-1>U<1,+besko.>. I sada ovo što ti se "nalazi" u Arcth ti mora biti iz tog intervala, odnoso , a domena od Arcth je ←besko.,-1>U<1,+besko.>. I sada ovo što ti se "nalazi" u Arcth ti mora biti iz tog intervala, odnoso 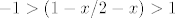 i rješiš nejednadžbu + ovdje imaš još jedan uvijet da ti x mora biti različito od 2. i rješiš nejednadžbu + ovdje imaš još jedan uvijet da ti x mora biti različito od 2.
i na kraju napraviš presjek od R-a i dobivenog intervala iz nejednadžbe. Eto nadam se da ti je jasnije malo.... *
Added after 5 minutes:
| Lepi91 (napisa): | f(x)=(1-3^x)/(2+3^x)
odredi sliku
odredi f(←besk.,0))
muci me to sa beskonacno...kak se to inace provijerava...mislim da bi rjesenje trebalo biti (0,1/2) al do toga sam dosao preko digitrona,koji nesmijemo iamti na kolokviju,pa ako mi ko moze reci kak se to inace racuna kad imamo beskonacno jer nemogu uvrstiti neki broj...
fala
i samo mi recite i sliku da usput provijerim jel mi dobro |
Meni ovako ispada;
Rf=<1/2,+besko.>
f(←besk.,0>)=[0,1/2>.
A kako da ti objasnim ovo sa beskonačnoću, a da bude efikasno stvarno ne bih znala, zato to preporučam vrsnijim matematičarima od mene....al savjet, nacrtaj grafove funkcija, ovu f-ju može prikazat kao kompoziciju dviju f-ja, pa se malo zagledaj u to, pa ti moža bude jasnije. 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 12:01 ned, 24. 10. 2010 Naslov: Postano: 12:01 ned, 24. 10. 2010 Naslov: |
    |
|
|
[quote="medonja"][quote="123456"]zanima me samo kak u 1. zadatku odredis domenu od arcth... i mislim da ti to nije kotangens vec tangens[/quote]
* Domena od arctg je cijeli [latex]R[/latex], a domena od Arcth je <-besko.,-1>U<1,+besko.>. I sada ovo što ti se "nalazi" u Arcth ti mora biti iz tog intervala, odnoso [latex]-1>(1-x/2-x)>1[/latex] i rješiš nejednadžbu + ovdje imaš još jedan uvijet da ti x mora biti različito od 2.
i na kraju napraviš presjek od R-a i dobivenog intervala iz nejednadžbe. Eto nadam se da ti je jasnije malo.... *
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote="Lepi91"]f(x)=(1-3^x)/(2+3^x)
odredi sliku
odredi f(<-besk.,0))
muci me to sa beskonacno...kak se to inace provijerava...mislim da bi rjesenje trebalo biti (0,1/2) al do toga sam dosao preko digitrona,koji nesmijemo iamti na kolokviju,pa ako mi ko moze reci kak se to inace racuna kad imamo beskonacno jer nemogu uvrstiti neki broj...
fala
i samo mi recite i sliku da usput provijerim jel mi dobro[/quote]
Meni ovako ispada;
Rf=<1/2,+besko.>
f(<-besk.,0>)=[0,1/2>.
A kako da ti objasnim ovo sa beskonačnoću, a da bude efikasno stvarno ne bih znala, zato to preporučam vrsnijim matematičarima od mene....al savjet, nacrtaj grafove funkcija, ovu f-ju može prikazat kao kompoziciju dviju f-ja, pa se malo zagledaj u to, pa ti moža bude jasnije. :P[/quote]
jel greska ako se napise <0.5,0]???
| medonja (napisa): | | 123456 (napisa): | | zanima me samo kak u 1. zadatku odredis domenu od arcth... i mislim da ti to nije kotangens vec tangens |
* Domena od arctg je cijeli 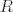 , a domena od Arcth je ←besko.,-1>U<1,+besko.>. I sada ovo što ti se "nalazi" u Arcth ti mora biti iz tog intervala, odnoso , a domena od Arcth je ←besko.,-1>U<1,+besko.>. I sada ovo što ti se "nalazi" u Arcth ti mora biti iz tog intervala, odnoso 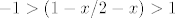 i rješiš nejednadžbu + ovdje imaš još jedan uvijet da ti x mora biti različito od 2. i rješiš nejednadžbu + ovdje imaš još jedan uvijet da ti x mora biti različito od 2.
i na kraju napraviš presjek od R-a i dobivenog intervala iz nejednadžbe. Eto nadam se da ti je jasnije malo.... *
Added after 5 minutes:
| Lepi91 (napisa): | f(x)=(1-3^x)/(2+3^x)
odredi sliku
odredi f(←besk.,0))
muci me to sa beskonacno...kak se to inace provijerava...mislim da bi rjesenje trebalo biti (0,1/2) al do toga sam dosao preko digitrona,koji nesmijemo iamti na kolokviju,pa ako mi ko moze reci kak se to inace racuna kad imamo beskonacno jer nemogu uvrstiti neki broj...
fala
i samo mi recite i sliku da usput provijerim jel mi dobro |
Meni ovako ispada;
Rf=<1/2,+besko.>
f(←besk.,0>)=[0,1/2>.
A kako da ti objasnim ovo sa beskonačnoću, a da bude efikasno stvarno ne bih znala, zato to preporučam vrsnijim matematičarima od mene....al savjet, nacrtaj grafove funkcija, ovu f-ju može prikazat kao kompoziciju dviju f-ja, pa se malo zagledaj u to, pa ti moža bude jasnije.  |
jel greska ako se napise <0.5,0]???
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
|






