|
Evo i treći i 2. a):
Dakle, treći. Prirodno je nekako očekivati da će se supremum postići za male [latex]m[/latex] i [latex]n[/latex]. To ćemo i dokazati: za [latex]m=n=1[/latex] dobivamo element [latex]\sqrt{3}[/latex], pa ćemo pokazati da za sve [latex]m,n\in\mathbb{N}[/latex] vrijedi [latex]\sqrt[(m+n)!]{n+2m}\leq \sqrt{3}[/latex]. Tada će očito vrijediti [latex]\sup A=\sqrt{3}[/latex].
Pa dobro: [latex]\displaystyle\sqrt[(m+n)!]{n+2m} \leq \sqrt{3}[/latex] je ekvivalentno s [latex]\displaystyle n+2m\leq 3^{\frac{(m+n)!}{2}[/latex]. Kako je [latex](m+n)!\geq m+n[/latex], a [latex]n+2m<2n+2m[/latex], dovoljno nam je pokazati [latex]\displaystyle 2n+2m\leq 3^{\frac{m+n}{2}[/latex]. Neka je sad [latex]t=m+n[/latex]. Tada zapravo (kad kvadriramo) želimo pokazati [latex]3^{t}\geq 4t^2[/latex]. Sad, indukcijom ili kako već lako se pokazuje da ta tvrdnja vrijedi za sve [latex]t\geq 4[/latex] (baza je jasna, a za takve [latex]t[/latex] [latex]3\cdot 4t^2\geq 4(t+1)^2[/latex] - samo riješi kvadratnu jednadžbu). Stoga, za [latex]m+n\geq 4[/latex] smo pokazali da vrijedi [latex]\displaystyle n+2m<2n+2m\leq 3^{\frac{m+n}{2}} \leq 3^{\frac{(m+n)!}{2}[/latex], čime smo gotovi. Preostaje [latex]t\leq 4[/latex]. No, tada je ili [latex]m=n=1[/latex] (gdje dobivamo [latex]\sqrt{3}[/latex]), ili je [latex](m,n)=(2,1)[/latex], gdje dobivamo [latex]\sqrt[6]{5}<\sqrt{3}[/latex], ili je [latex](m,n)=(2,1)[/latex], što daje [latex]\sqrt[6]{4}<\sqrt{3}[/latex]. Stoga, najveći član ovog skupa i ujedno supremum je [latex]\sqrt{3}[/latex].
Infimum je lagan: očito su svi elementi veći ili jednaki [latex]1[/latex]. Sad uzmi niz članova koji dobivamo za [latex]m=n[/latex]. Tad imamo [latex]a_n=\sqrt[(2n)!]{3n}<\sqrt[n]{3n}[/latex], pa ovaj niz očito konvergira u jedinicu. Dakle, [latex]\inf A=1[/latex].
Idemo sad na 2. a). Ovaj niz zapravo može imati svega nekoliko različitih članova. To ćemo i dokazati. :)
Primijeti da nam [latex]n^2[/latex] može davati ostatke [latex]0,1,2,4[/latex] pri dijeljenju sa [latex]7[/latex]. (To lako provjeriš gledanjem svih mogućih ostataka [latex]n[/latex] pri dijeljenju sa [latex]7[/latex]. Stoga, [latex]2n^2[/latex] može davati ostatke [latex]0,2,4,8\equiv 1[/latex] pri dijeljenju sa [latex]7[/latex]. Dakle, [latex]\displaystyle\frac{2n^2}{7}[/latex] može biti oblika [latex]\displaystyle\frac{7k}{7}=k[/latex], [latex]\displaystyle\frac{7k+1}{7}=k+\frac{1}{7}[/latex], [latex]\displaystyle\frac{7k+2}{7}=k+\frac{2}{7}[/latex] ili [latex]\displaystyle\frac{7k+4}{7}=k+\frac{4}{7}[/latex], pri čemu je [latex]k[/latex] cijeli broj (i, primijetimo, iznosi baš [latex]\lfloor\displaystyle\frac{2n^2}{7}\rfloor[/latex]). Dakle, [latex]\displaystyle\frac{2n^2}{7}-\lfloor \frac{2n^2}{7}\rfloor[/latex] je uvijek iz skupa [latex]\displaystyle \{0,\frac{1}{7},\frac{2}{7},\frac{4}{7}\}[/latex]. Kako za beskonačno mnogo članova (npr. za sve [latex]n=7l+3[/latex]) možemo postići četiri sedmine, upravo je to najveće gomilište.
Evo, nisam možda bio precizan koliko se tražilo na kolokvijima :P, ali mislim da shvaćaš poantu. :)
Evo i treći i 2. a):
Dakle, treći. Prirodno je nekako očekivati da će se supremum postići za male 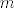 i i  . To ćemo i dokazati: za . To ćemo i dokazati: za  dobivamo element dobivamo element  , pa ćemo pokazati da za sve , pa ćemo pokazati da za sve 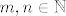 vrijedi vrijedi  . Tada će očito vrijediti . Tada će očito vrijediti 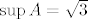 . .
Pa dobro: 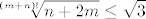 je ekvivalentno s je ekvivalentno s 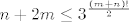 . Kako je . Kako je 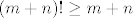 , a , a  , dovoljno nam je pokazati , dovoljno nam je pokazati 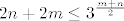 . Neka je sad . Neka je sad 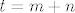 . Tada zapravo (kad kvadriramo) želimo pokazati . Tada zapravo (kad kvadriramo) želimo pokazati  . Sad, indukcijom ili kako već lako se pokazuje da ta tvrdnja vrijedi za sve . Sad, indukcijom ili kako već lako se pokazuje da ta tvrdnja vrijedi za sve 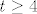 (baza je jasna, a za takve (baza je jasna, a za takve  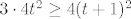 - samo riješi kvadratnu jednadžbu). Stoga, za - samo riješi kvadratnu jednadžbu). Stoga, za 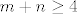 smo pokazali da vrijedi smo pokazali da vrijedi 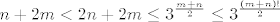 , čime smo gotovi. Preostaje , čime smo gotovi. Preostaje 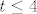 . No, tada je ili . No, tada je ili  (gdje dobivamo (gdje dobivamo  ), ili je ), ili je  , gdje dobivamo , gdje dobivamo  , ili je , ili je  , što daje , što daje 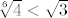 . Stoga, najveći član ovog skupa i ujedno supremum je . Stoga, najveći član ovog skupa i ujedno supremum je  . .
Infimum je lagan: očito su svi elementi veći ili jednaki 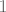 . Sad uzmi niz članova koji dobivamo za . Sad uzmi niz članova koji dobivamo za  . Tad imamo . Tad imamo 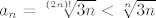 , pa ovaj niz očito konvergira u jedinicu. Dakle, , pa ovaj niz očito konvergira u jedinicu. Dakle,  . .
Idemo sad na 2. a). Ovaj niz zapravo može imati svega nekoliko različitih članova. To ćemo i dokazati. 
Primijeti da nam 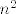 može davati ostatke može davati ostatke 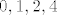 pri dijeljenju sa pri dijeljenju sa 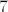 . (To lako provjeriš gledanjem svih mogućih ostataka . (To lako provjeriš gledanjem svih mogućih ostataka  pri dijeljenju sa pri dijeljenju sa 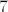 . Stoga, . Stoga, 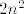 može davati ostatke može davati ostatke 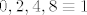 pri dijeljenju sa pri dijeljenju sa 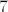 . Dakle, . Dakle,  može biti oblika može biti oblika 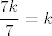 , , 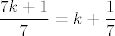 , , 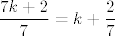 ili ili  , pri čemu je , pri čemu je 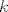 cijeli broj (i, primijetimo, iznosi baš cijeli broj (i, primijetimo, iznosi baš 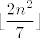 ). Dakle, ). Dakle,  je uvijek iz skupa je uvijek iz skupa 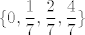 . Kako za beskonačno mnogo članova (npr. za sve . Kako za beskonačno mnogo članova (npr. za sve 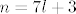 ) možemo postići četiri sedmine, upravo je to najveće gomilište. ) možemo postići četiri sedmine, upravo je to najveće gomilište.
Evo, nisam možda bio precizan koliko se tražilo na kolokvijima  , ali mislim da shvaćaš poantu. , ali mislim da shvaćaš poantu. 
|





