| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 13:43 pon, 27. 12. 2010 Naslov: Postano: 13:43 pon, 27. 12. 2010 Naslov: |
    |
|
|
Ovaj prvi nema neke pretjerane veze s implicitno zadanim funkcijama, ali ok. Neka je [latex]f : \mathbb{R}^3 \to \mathbb{R}^2[/latex] definirana s [latex]f(x, y, z) = (x y^3 z, x^2 + y^2)[/latex]. Očito je [latex]g = F \circ f[/latex]. Funkcije [latex]F[/latex] i [latex]f[/latex] su diferencijabilne (prva zato što tako kaže zadatak, druga zato što joj je svaka komponenta polinom), pa je i [latex]g[/latex] diferencijabilna. Preostaje odrediti [latex]\nabla g(x, y, z)[/latex], ali po teoremu o diferencijalu kompozicije slijedi da je [latex]\nabla g(x, y, z) = \nabla F(f(x, y, z)) \cdot \nabla f(x, y, z)[/latex]. Znamo odrediti [latex]\nabla f(x, y, z)[/latex], ali [latex]\nabla F(f(x, y, z))[/latex] trebamo ostaviti.
Sad na drugi. Definiramo [latex]F : \mathbb{R}^2 \to \mathbb{R}[/latex] s [latex]F(x, y) = x^2 y^3 + 2 y - \cos y[/latex]. Uočimo da je [latex]F[/latex] klase [latex]C^1[/latex] (treba nam za primjenu teorema o implicitnoj funkciji).
Treba pokazati da postoji jedinstvena funkcija [latex]f : \mathbb{R} \to \mathbb{R}[/latex] klase [latex]C^1[/latex] td. [latex]F(x, f(x)) = 0[/latex] za svaki [latex]x \in \mathbb{R}[/latex]. Da dokažemo samo da postoji jedinstvena funkcija (bez tvrdnje koje je klase) koja zadovoljava to svojstvo, dovoljno nam je znanje MA. Teorem o implicitnoj funkciji nam je potreban da pokažemo da je ta funkcija doista klase [latex]C^1[/latex]. Primijetimo da ne možemo odmah skočiti na taj drugi korak, jer se u teoremu o implicitnoj funkciji zahtijeva postojanje točke [latex](x_0, y_0)[/latex] koja zadovoljava [latex]F(x_0, y_0) = 0[/latex], što u biti znači postojanje funkcije [latex]x_0 \mapsto y_0[/latex]. Krenimo!
Dokažimo da za proizvoljan [latex]x_0 \in \mathbb{R}[/latex] postoji jedinstveni [latex]y_0 \in \mathbb{R}[/latex] td. [latex]F(x_0, y_0) = 0[/latex]. Definiramo [latex]F_{x_0} : \mathbb{R} \to \mathbb{R}[/latex] s [latex]F_{x_0}(y) = x_0^2 y^3 + 2 y - \cos y[/latex]. Trebamo pokazati da funkcija [latex]F_{x_0}[/latex] ima jedinstvenu nultočku. Vidimo da je [latex]\displaystyle \lim_{y \to \pm \infty} F_{x_0}(y) = \pm \infty[/latex], pa zbog neprekidnosti funkcije [latex]F_{x_0}[/latex] slijedi ona ima nultočku. Preostaje pokazati da je jedinstvena. Uočimo [latex]F'_{x_0}(y) = 3 x_0^2 y^2 + 2 + \sin y \geq 0 + 2 - 1 = 1 > 0[/latex], što povlači da je [latex]F_{x_0}[/latex] strogo rastuća, a time i injekcija. Dakle, postoji jedinstvena točka [latex]y_0 \in \mathbb{R}[/latex] td. je [latex]F_{x_0}(y_0) = F(x_0, y_0) = 0[/latex]. Definiramo [latex]f(x_0) = y_0[/latex]. Time smo odredili funkciju [latex]f[/latex].
Dokažimo da je [latex]f \in C^1[/latex]. Uzmimo proizvoljni [latex]x_0 \in \mathbb{R}[/latex] i pripadni [latex]y_0 \in \mathbb{R}[/latex] td. [latex]F(x_0, y_0) = 0[/latex]. Znamo da je [latex]F \in C^1[/latex] i da je [latex]\displaystyle \frac{\partial F}{\partial y}(x, y) = \left[ 3 x^2 y^2 + 2 + \sin y \right][/latex] regularna matrica (determinanta različita od 0). Po [b]teoremu[/b] [size=7]drumroll[/size] [b]o[/b] [size=7]drumroll[/size] [b]implicitnoj[/b] [size=7]drumroll[/size] [b]funkciji[/b] slijedi da postoji okolina [latex]U[/latex] točke [latex]x_0[/latex], okolina [latex]V[/latex] točke [latex]y_0[/latex] i jedinstvena funkcija [latex]f_{x_0} : U \to V[/latex] klase [latex]C^1[/latex] td. [latex]F(x, f_{x_0}(x)) = 0[/latex], za svaki [latex]x \in U[/latex]. No, kako je [latex]f[/latex] jedinstvena, slijedi da je [latex]f(x) = f_{x_0}(x)[/latex] za sve [latex]x \in U[/latex]. To znači da je [latex]f[/latex] klase [latex]C^1[/latex] na okolini (proizvoljne) točke [latex]x_0[/latex]. Slijedi da je [latex]f[/latex] klase [latex]C^1[/latex].
Ovaj prvi nema neke pretjerane veze s implicitno zadanim funkcijama, ali ok. Neka je 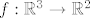 definirana s definirana s 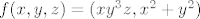 . Očito je . Očito je 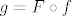 . Funkcije . Funkcije 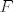 i i  su diferencijabilne (prva zato što tako kaže zadatak, druga zato što joj je svaka komponenta polinom), pa je i su diferencijabilne (prva zato što tako kaže zadatak, druga zato što joj je svaka komponenta polinom), pa je i  diferencijabilna. Preostaje odrediti diferencijabilna. Preostaje odrediti 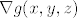 , ali po teoremu o diferencijalu kompozicije slijedi da je , ali po teoremu o diferencijalu kompozicije slijedi da je 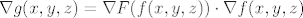 . Znamo odrediti . Znamo odrediti 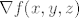 , ali , ali 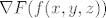 trebamo ostaviti. trebamo ostaviti.
Sad na drugi. Definiramo 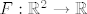 s s 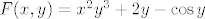 . Uočimo da je . Uočimo da je 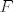 klase klase 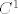 (treba nam za primjenu teorema o implicitnoj funkciji). (treba nam za primjenu teorema o implicitnoj funkciji).
Treba pokazati da postoji jedinstvena funkcija 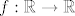 klase klase 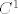 td. td. 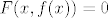 za svaki za svaki 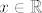 . Da dokažemo samo da postoji jedinstvena funkcija (bez tvrdnje koje je klase) koja zadovoljava to svojstvo, dovoljno nam je znanje MA. Teorem o implicitnoj funkciji nam je potreban da pokažemo da je ta funkcija doista klase . Da dokažemo samo da postoji jedinstvena funkcija (bez tvrdnje koje je klase) koja zadovoljava to svojstvo, dovoljno nam je znanje MA. Teorem o implicitnoj funkciji nam je potreban da pokažemo da je ta funkcija doista klase 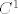 . Primijetimo da ne možemo odmah skočiti na taj drugi korak, jer se u teoremu o implicitnoj funkciji zahtijeva postojanje točke . Primijetimo da ne možemo odmah skočiti na taj drugi korak, jer se u teoremu o implicitnoj funkciji zahtijeva postojanje točke 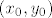 koja zadovoljava koja zadovoljava 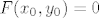 , što u biti znači postojanje funkcije , što u biti znači postojanje funkcije 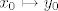 . Krenimo! . Krenimo!
Dokažimo da za proizvoljan 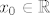 postoji jedinstveni postoji jedinstveni 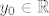 td. td. 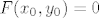 . Definiramo . Definiramo 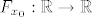 s s 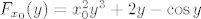 . Trebamo pokazati da funkcija . Trebamo pokazati da funkcija 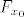 ima jedinstvenu nultočku. Vidimo da je ima jedinstvenu nultočku. Vidimo da je 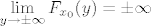 , pa zbog neprekidnosti funkcije , pa zbog neprekidnosti funkcije 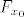 slijedi ona ima nultočku. Preostaje pokazati da je jedinstvena. Uočimo slijedi ona ima nultočku. Preostaje pokazati da je jedinstvena. Uočimo 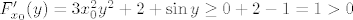 , što povlači da je , što povlači da je 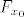 strogo rastuća, a time i injekcija. Dakle, postoji jedinstvena točka strogo rastuća, a time i injekcija. Dakle, postoji jedinstvena točka 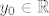 td. je td. je 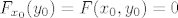 . Definiramo . Definiramo 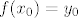 . Time smo odredili funkciju . Time smo odredili funkciju  . .
Dokažimo da je 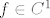 . Uzmimo proizvoljni . Uzmimo proizvoljni 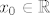 i pripadni i pripadni 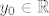 td. td. 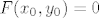 . Znamo da je . Znamo da je 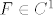 i da je i da je 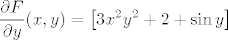 regularna matrica (determinanta različita od 0). Po teoremu drumroll o drumroll implicitnoj drumroll funkciji slijedi da postoji okolina regularna matrica (determinanta različita od 0). Po teoremu drumroll o drumroll implicitnoj drumroll funkciji slijedi da postoji okolina 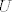 točke točke  , okolina , okolina 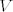 točke točke 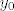 i jedinstvena funkcija i jedinstvena funkcija 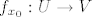 klase klase 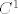 td. td. 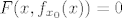 , za svaki , za svaki 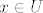 . No, kako je . No, kako je  jedinstvena, slijedi da je jedinstvena, slijedi da je 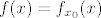 za sve za sve 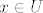 . To znači da je . To znači da je  klase klase 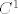 na okolini (proizvoljne) točke na okolini (proizvoljne) točke  . Slijedi da je . Slijedi da je  klase klase 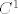 . .
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 11:17 uto, 28. 12. 2010 Naslov: Postano: 11:17 uto, 28. 12. 2010 Naslov: |
    |
|
|
Hvala!!!
[quote="pmli"]
Definiramo [latex]F_{x_0} : \mathbb{R} \to \mathbb{R}[/latex] s [latex]F_{x_0}(y) = x_0^2 y^3 + 2 y - \cos y[/latex].[/quote]
uvijek na ovaj način definiramo funkciju?tj,ono što nam je f(x) nam je varijabla,a ostalo konstante? ako razumiješ što želim reći,tako smo i na vježbama radili!
[quote="pmli"]
Trebamo pokazati da funkcija [latex]F_{x_0}[/latex] ima jedinstvenu nultočku. Vidimo da je [latex]\displaystyle \lim_{y \to \pm \infty} F_{x_0}(y) = \pm \infty[/latex], pa zbog neprekidnosti funkcije [latex]F_{x_0}[/latex] slijedi ona ima nultočku. Preostaje pokazati da je jedinstvena. Uočimo [latex]F'_{x_0}(y) = 3 x_0^2 y^2 + 2 + \sin y \geq 0 + 2 - 1 = 1 > 0[/latex], što povlači da je [latex]F_{x_0}[/latex] strogo rastuća, a time i injekcija. Dakle, postoji jedinstvena točka [latex]y_0 \in \mathbb{R}[/latex] td. je [latex]F_{x_0}(y_0) = F(x_0, y_0) = 0[/latex].[/quote]
ovo također,postoji li neki drugi način da se odredi je li točka jedinstvena(samo smo ovako radili i na vježbama pa nisam sigurna)
http://web.math.hr/nastava/difraf/dif/vjezbe9c.pdf
i zanima me kako smo u zadatku 1.4. da je F(1,0,1,1)=0?
Hvala!!!
| pmli (napisa): |
Definiramo 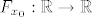 s s 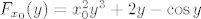 . . |
uvijek na ovaj način definiramo funkciju?tj,ono što nam je f(x) nam je varijabla,a ostalo konstante? ako razumiješ što želim reći,tako smo i na vježbama radili!
| pmli (napisa): |
Trebamo pokazati da funkcija 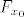 ima jedinstvenu nultočku. Vidimo da je ima jedinstvenu nultočku. Vidimo da je 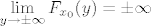 , pa zbog neprekidnosti funkcije , pa zbog neprekidnosti funkcije 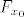 slijedi ona ima nultočku. Preostaje pokazati da je jedinstvena. Uočimo slijedi ona ima nultočku. Preostaje pokazati da je jedinstvena. Uočimo 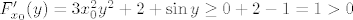 , što povlači da je , što povlači da je 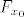 strogo rastuća, a time i injekcija. Dakle, postoji jedinstvena točka strogo rastuća, a time i injekcija. Dakle, postoji jedinstvena točka 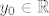 td. je td. je 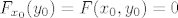 . . |
ovo također,postoji li neki drugi način da se odredi je li točka jedinstvena(samo smo ovako radili i na vježbama pa nisam sigurna)
http://web.math.hr/nastava/difraf/dif/vjezbe9c.pdf
i zanima me kako smo u zadatku 1.4. da je F(1,0,1,1)=0?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 16:46 uto, 28. 12. 2010 Naslov: Postano: 16:46 uto, 28. 12. 2010 Naslov: |
    |
|
|
[quote=".anchy."]uvijek na ovaj način definiramo funkciju?tj,ono što nam je f(x) nam je varijabla,a ostalo konstante? ako razumiješ što želim reći,tako smo i na vježbama radili![/quote]
Iskreno, ne razumijem te u potpunosti. "Uvijek" je jaka riječ. Pročitaj si ponovo zadatak i što se traži. Što znači da postoji jedinstvena funkcija? To znači da za svaki x postoji jedinstven y td. nešto vrijedi. Da to dokažemo, uzmemo proizvoljan, fiksan x, i promatramo što se događa kad mijenjamo y. Dakle, fiksirali smo x, a y je ostao varijabilan. Sad smo sretni, jer smo dobili realnu funkciju realne varijable na koje smo navikli. :w00t:
Ono što pokušavam objasniti je da, kad vidiš neki zadatak koji imalo smrdi po teoremu o implicitnoj funkciji, ne kreneš tražiti funkcije više varijable koje bi mogla pretvoriti u funkcije jedne varijable. Razmisli što se traži prije nego nastaviš. :)
[quote=".anchy."]ovo također,postoji li neki drugi način da se odredi je li točka jedinstvena(samo smo ovako radili i na vježbama pa nisam sigurna)[/quote]
Vjerojatno postoji, ali zašto se brinuti oko toga? Funkcija je diferencijabilna i koristeći to možemo elegantno odrediti raste li ili pada (i time je li injekcija).
[quote=".anchy."]http://web.math.hr/nastava/difraf/dif/vjezbe9c.pdf
i zanima me kako smo u zadatku 1.4. da je F(1,0,1,1)=0?[/quote]
Imam osjećaj da si zaboravila neki glagol. :) kako smo... što? Dokazali, skužili? Kad uvrstiš te brojeve, dobi se 0. Točke (1,0) i (1,1) su ti zadane, pa je razumljivo da se baš njih uvrsti. :)
| .anchy. (napisa): | | uvijek na ovaj način definiramo funkciju?tj,ono što nam je f(x) nam je varijabla,a ostalo konstante? ako razumiješ što želim reći,tako smo i na vježbama radili! |
Iskreno, ne razumijem te u potpunosti. "Uvijek" je jaka riječ. Pročitaj si ponovo zadatak i što se traži. Što znači da postoji jedinstvena funkcija? To znači da za svaki x postoji jedinstven y td. nešto vrijedi. Da to dokažemo, uzmemo proizvoljan, fiksan x, i promatramo što se događa kad mijenjamo y. Dakle, fiksirali smo x, a y je ostao varijabilan. Sad smo sretni, jer smo dobili realnu funkciju realne varijable na koje smo navikli. 
Ono što pokušavam objasniti je da, kad vidiš neki zadatak koji imalo smrdi po teoremu o implicitnoj funkciji, ne kreneš tražiti funkcije više varijable koje bi mogla pretvoriti u funkcije jedne varijable. Razmisli što se traži prije nego nastaviš. 
| .anchy. (napisa): | | ovo također,postoji li neki drugi način da se odredi je li točka jedinstvena(samo smo ovako radili i na vježbama pa nisam sigurna) |
Vjerojatno postoji, ali zašto se brinuti oko toga? Funkcija je diferencijabilna i koristeći to možemo elegantno odrediti raste li ili pada (i time je li injekcija).
| .anchy. (napisa): | http://web.math.hr/nastava/difraf/dif/vjezbe9c.pdf
i zanima me kako smo u zadatku 1.4. da je F(1,0,1,1)=0? |
Imam osjećaj da si zaboravila neki glagol.  kako smo... što? Dokazali, skužili? Kad uvrstiš te brojeve, dobi se 0. Točke (1,0) i (1,1) su ti zadane, pa je razumljivo da se baš njih uvrsti. kako smo... što? Dokazali, skužili? Kad uvrstiš te brojeve, dobi se 0. Točke (1,0) i (1,1) su ti zadane, pa je razumljivo da se baš njih uvrsti. 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 19:04 uto, 28. 12. 2010 Naslov: Postano: 19:04 uto, 28. 12. 2010 Naslov: |
    |
|
|
[quote="pmli"]Imam osjećaj da si zaboravila neki glagol. :) kako smo... što? Dokazali, skužili? Kad uvrstiš te brojeve, dobi se 0. Točke (1,0) i (1,1) su ti zadane, pa je razumljivo da se baš njih uvrsti. :)[/quote]
:lol:
da,jesam,glagol je dobili,ali si mi i odgovorio na to pitanje.isto tako i ono prvo pitanje sam shvatila,a i drugo,pa ti puuunooooo hvala!!!!!
| pmli (napisa): | Imam osjećaj da si zaboravila neki glagol.  kako smo... što? Dokazali, skužili? Kad uvrstiš te brojeve, dobi se 0. Točke (1,0) i (1,1) su ti zadane, pa je razumljivo da se baš njih uvrsti. kako smo... što? Dokazali, skužili? Kad uvrstiš te brojeve, dobi se 0. Točke (1,0) i (1,1) su ti zadane, pa je razumljivo da se baš njih uvrsti.  |

da,jesam,glagol je dobili,ali si mi i odgovorio na to pitanje.isto tako i ono prvo pitanje sam shvatila,a i drugo,pa ti puuunooooo hvala!!!!!
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
|











