| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
 Postano: 18:08 sub, 23. 10. 2010 Naslov: Kolokvij 2006. Postano: 18:08 sub, 23. 10. 2010 Naslov: Kolokvij 2006. |
    |
|
|
Moze li mi netko pomoci oko ovih zadataka?
1.f(x)=arctg( (1-x)/x). f(<0,+bes>, f([1/2, 1>)
2. f(x)=e^-ln^2x + 5lnx-6. f^-1([1,e>)
3. Prirodna domena funkcije
osmi korijen( log5(x)+1/log5(x)-2)
Moze samo hintovi, al bih voli i rjesenja da mogu provjeriti. Puno hvala :D
Moze li mi netko pomoci oko ovih zadataka?
1.f(x)=arctg( (1-x)/x). f(<0,+bes>, f([1/2, 1>)
2. f(x)=e^-ln^2x + 5lnx-6. f^-1([1,e>)
3. Prirodna domena funkcije
osmi korijen( log5(x)+1/log5(x)-2)
Moze samo hintovi, al bih voli i rjesenja da mogu provjeriti. Puno hvala 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 18:36 sub, 23. 10. 2010 Naslov: Re: Kolokvij 2006. Postano: 18:36 sub, 23. 10. 2010 Naslov: Re: Kolokvij 2006. |
    |
|
|
[quote="CROmpir"]Moze li mi netko pomoci oko ovih zadataka?
1.f(x)=arctg( (1-x)/x). f(<0,+bes>, f([1/2, 1>)
2. f(x)=e^-ln^2x + 5lnx-6. f^-1([1,e>)
3. Prirodna domena funkcije
osmi korijen( log5(x)+1/log5(x)-2)
Moze samo hintovi, al bih voli i rjesenja da mogu provjeriti. Puno hvala :D[/quote]
znaci ovako:
2. trazimo kada je ta vrijednost jednaka 1,to znaci kada je eksponent jednak nuli -ln^2x + 5lnx-6=0
sad napravis supstituciju: t=lnx i dobis kvadratnu jednadzbu -a^2+5a-6=0
analogno kad je ta vrijednost jednaka e,kada je eksponent jednak 1
isti postupak
3.
1)x mora biti razlicit od 2
2)izraz pod korijenom mora biti >= 0
3) x+1>0
x-2>0
domena ti je presjek svih tih rjesenja
a prvi nek ti netko od starijih pomogne malo je za mene kompliciran zgob ovog beskonacno u a) jer neznam kak bi to
| CROmpir (napisa): | Moze li mi netko pomoci oko ovih zadataka?
1.f(x)=arctg( (1-x)/x). f(<0,+bes>, f([1/2, 1>)
2. f(x)=e^-ln^2x + 5lnx-6. f^-1([1,e>)
3. Prirodna domena funkcije
osmi korijen( log5(x)+1/log5(x)-2)
Moze samo hintovi, al bih voli i rjesenja da mogu provjeriti. Puno hvala  |
znaci ovako:
2. trazimo kada je ta vrijednost jednaka 1,to znaci kada je eksponent jednak nuli -ln^2x + 5lnx-6=0
sad napravis supstituciju: t=lnx i dobis kvadratnu jednadzbu -a^2+5a-6=0
analogno kad je ta vrijednost jednaka e,kada je eksponent jednak 1
isti postupak
3.
1)x mora biti razlicit od 2
2)izraz pod korijenom mora biti >= 0
3) x+1>0
x-2>0
domena ti je presjek svih tih rjesenja
a prvi nek ti netko od starijih pomogne malo je za mene kompliciran zgob ovog beskonacno u a) jer neznam kak bi to
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 18:52 sub, 23. 10. 2010 Naslov: Re: Kolokvij 2006. Postano: 18:52 sub, 23. 10. 2010 Naslov: Re: Kolokvij 2006. |
    |
|
|
[quote="Lepi91"][quote="CROmpir"]Moze li mi netko pomoci oko ovih zadataka?
1.f(x)=arctg( (1-x)/x). f(<0,+bes>, f([1/2, 1>)
2. f(x)=e^-ln^2x + 5lnx-6. f^-1([1,e>)
3. Prirodna domena funkcije
osmi korijen( log5(x)+1/log5(x)-2)
Moze samo hintovi, al bih voli i rjesenja da mogu provjeriti. Puno hvala :D[/quote]
znaci ovako:
2. trazimo kada je ta vrijednost jednaka 1,to znaci kada je eksponent jednak nuli -ln^2x + 5lnx-6=0
sad napravis supstituciju: t=lnx i dobis kvadratnu jednadzbu -a^2+5a-6=0
analogno kad je ta vrijednost jednaka e,kada je eksponent jednak 1
isti postupak
3.
[color=red]1)x mora biti razlicit od 2[/color]
2)izraz pod korijenom mora biti >= 0
3) x+1>0
x-2>0
domena ti je presjek svih tih rjesenja
a prvi nek ti netko od starijih pomogne malo je za mene kompliciran zgob ovog beskonacno u a) jer neznam kak bi to[/quote]
Ovo log5(x)-2 treba biti različito od nule, a ne samo 2....
| Lepi91 (napisa): | | CROmpir (napisa): | Moze li mi netko pomoci oko ovih zadataka?
1.f(x)=arctg( (1-x)/x). f(<0,+bes>, f([1/2, 1>)
2. f(x)=e^-ln^2x + 5lnx-6. f^-1([1,e>)
3. Prirodna domena funkcije
osmi korijen( log5(x)+1/log5(x)-2)
Moze samo hintovi, al bih voli i rjesenja da mogu provjeriti. Puno hvala  |
znaci ovako:
2. trazimo kada je ta vrijednost jednaka 1,to znaci kada je eksponent jednak nuli -ln^2x + 5lnx-6=0
sad napravis supstituciju: t=lnx i dobis kvadratnu jednadzbu -a^2+5a-6=0
analogno kad je ta vrijednost jednaka e,kada je eksponent jednak 1
isti postupak
3.
1)x mora biti razlicit od 2
2)izraz pod korijenom mora biti >= 0
3) x+1>0
x-2>0
domena ti je presjek svih tih rjesenja
a prvi nek ti netko od starijih pomogne malo je za mene kompliciran zgob ovog beskonacno u a) jer neznam kak bi to |
Ovo log5(x)-2 treba biti različito od nule, a ne samo 2....
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 19:29 sub, 23. 10. 2010 Naslov: Postano: 19:29 sub, 23. 10. 2010 Naslov: |
    |
|
|
[quote="CROmpir"]Okej, sad sam skuzio 2. al kolko vam rjesenje na kraju ispada?
i 3. btw, mislim da mora biti log5(x)-2<>0 a ne 2. Pa ispada da nesmije biti 25. ako se ne varam?[/quote]
gore sam napisala, nije dobro stavio, da je x različit od nule, taj uvijet u ovom zadatku ne postoji, nego da je log5(x)-2 [color=red]RAZLIČITO[/color] od nule... cijeli taj izraz mora biti raz od nule,...a za rješenja nemam pojma, nisam rješavala :D ak će mi se dat, javim kaj mi je ispalo....
| CROmpir (napisa): | Okej, sad sam skuzio 2. al kolko vam rjesenje na kraju ispada?
i 3. btw, mislim da mora biti log5(x)-2<>0 a ne 2. Pa ispada da nesmije biti 25. ako se ne varam? |
gore sam napisala, nije dobro stavio, da je x različit od nule, taj uvijet u ovom zadatku ne postoji, nego da je log5(x)-2 RAZLIČITO od nule... cijeli taj izraz mora biti raz od nule,...a za rješenja nemam pojma, nisam rješavala  ak će mi se dat, javim kaj mi je ispalo.... ak će mi se dat, javim kaj mi je ispalo....
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 19:51 sub, 23. 10. 2010 Naslov: Postano: 19:51 sub, 23. 10. 2010 Naslov: |
    |
|
|
Ustvari još bolja ideja, kad dobiješ nejednadžbu koristi supstituciju, npr. [latex]t=log_5(x)[/latex] :P
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="CROmpir"]Na kraju dobijem x>25.[/quote]
x je različit od 25.... [color=red]MORA BIT RAZLIČIT :D[/color]
a nejednadžbu mi se trenutno ne da rješavat 8)
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
Pošto sad gledam već u taj zadatak, MISLIM da je D_f=[1,+besko.>\{25}jer ako koristimo supstituciju dobimo neš tipa t^2+1, a rješenja su konjugirano kompleksna, a još moramo gledat da je x jednak ili veći 1 ...i bla
Ustvari još bolja ideja, kad dobiješ nejednadžbu koristi supstituciju, npr. 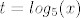 
Added after 1 minutes:
| CROmpir (napisa): | | Na kraju dobijem x>25. |
x je različit od 25.... MORA BIT RAZLIČIT 
a nejednadžbu mi se trenutno ne da rješavat 
Added after 5 minutes:
Pošto sad gledam već u taj zadatak, MISLIM da je D_f=[1,+besko.>\{25}jer ako koristimo supstituciju dobimo neš tipa t^2+1, a rješenja su konjugirano kompleksna, a još moramo gledat da je x jednak ili veći 1 ...i bla
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 11:01 ned, 24. 10. 2010 Naslov: Postano: 11:01 ned, 24. 10. 2010 Naslov: |
    |
|
|
Čisto jedno upozorenje na temelju nečega što je rekao Lepi, a što me sad podsjetilo. Ne kažem da itko tu radi tu grešku, ali ajde... prirodno je razmišljati na taj način, pa da skrenem pažnju. :D
Recimo da je [latex]f(x)=x^2[/latex] i da se traži [latex]f(\[-1,2\])[/latex]. E, sad, ako to idete računati na način "rub intervala uvijek se preslika u rub" (u smislu "izračunat ću u što ode [latex]-1[/latex], a u što [latex]2[/latex], pa spojiti te dvije točke"), to će otići kvragu. Naime, [latex]f(-1)=1[/latex], a [latex]f(2)=4[/latex]. Stoga bismo "izračunali" da je [latex]f(\[-1,2\])=\[1,4\][/latex]. No, to ne stoji - s grafa se sasvim razumno vidi da je traženo rješenje [latex]\[0,4\][/latex]. Daklem, nemojte tako računati. :)
A što se tiče prvog zadatka iz opening posta, vidim da nitko još nije odgovorio. U svakom slučaju, stvar je relativno jasna, [latex]f[/latex] shvatiš kao kompoziciju funkcija [latex]\arctan x[/latex], [latex]x-1[/latex] i [latex]\displaystyle\frac{1}{x}[/latex] i sad računaš slike preko te kompozicije. Rješenja su sad valjda [latex]\langle -\displaystyle\frac{\pi}{4},\displaystyle\frac{\pi}{2}\rangle[/latex] i [latex]\langle 0, \displaystyle\frac{\pi}{4}\][/latex], ali to sam malo napamet računao, tako da sam se možda zeznuo.
Čisto jedno upozorenje na temelju nečega što je rekao Lepi, a što me sad podsjetilo. Ne kažem da itko tu radi tu grešku, ali ajde... prirodno je razmišljati na taj način, pa da skrenem pažnju. 
Recimo da je 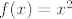 i da se traži i da se traži 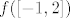 . E, sad, ako to idete računati na način "rub intervala uvijek se preslika u rub" (u smislu "izračunat ću u što ode . E, sad, ako to idete računati na način "rub intervala uvijek se preslika u rub" (u smislu "izračunat ću u što ode  , a u što , a u što  , pa spojiti te dvije točke"), to će otići kvragu. Naime, , pa spojiti te dvije točke"), to će otići kvragu. Naime, 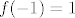 , a , a 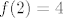 . Stoga bismo "izračunali" da je . Stoga bismo "izračunali" da je 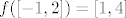 . No, to ne stoji - s grafa se sasvim razumno vidi da je traženo rješenje . No, to ne stoji - s grafa se sasvim razumno vidi da je traženo rješenje 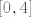 . Daklem, nemojte tako računati. . Daklem, nemojte tako računati. 
A što se tiče prvog zadatka iz opening posta, vidim da nitko još nije odgovorio. U svakom slučaju, stvar je relativno jasna,  shvatiš kao kompoziciju funkcija shvatiš kao kompoziciju funkcija 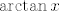 , , 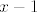 i i 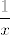 i sad računaš slike preko te kompozicije. Rješenja su sad valjda i sad računaš slike preko te kompozicije. Rješenja su sad valjda 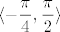 i i 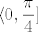 , ali to sam malo napamet računao, tako da sam se možda zeznuo. , ali to sam malo napamet računao, tako da sam se možda zeznuo.
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:50 pon, 25. 10. 2010 Naslov: Postano: 20:50 pon, 25. 10. 2010 Naslov: |
    |
|
|
Dobro, znam da su kolokviji prošli, ali nije to valjda razlog da vas prestanu zanimati rješenja zadataka? :P
Uglavnom, da, nije baš najtrivijalniji zadatak (barem ovako, bez derivacija), sjećam ga se još iz doba (:djed:) dok sam ja bio na prvoj godini. :) Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju.
No, ajde da vidimo. Neka je [latex]f(x)[/latex] funkcija s lijeve strane jednadžbe. Očito vrijedi [latex]-\displaystyle\frac{\pi}{2}<f(x)<\displaystyle\frac{3\pi}{2}[/latex]. To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi [latex]\cot (f(x))=0[/latex], imat ćemo da je [latex]f(x)=\displaystyle\frac{\pi}{2}[/latex]. (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo [latex]\displaystyle\frac{\pi}{2}[/latex].)
No dobro, ajde. Dakle, kotangensujmo to i sad idemo po adicijskim formulama za kotangens. Njih se da izvesti, a i relativno su poznate. Dakle, imamo [latex]\cot f(x)=\cot (\arctan x+\mathrm{arccot} x)=\displaystyle\frac{\cot (\arctan x)\cot(\mathrm{arccot} x)-1}{\cot (\arctan x)+\cot(\mathrm{arccot} x)}[/latex]. Sad koristimo da je [latex]\cot(\arctan x)=\displaystyle\frac{1}{\tan(\arctan x)}=\displaystyle\frac{1}{x}[/latex] (pri čemu to ima smisla samo za [latex]x\neq 0[/latex], ali za [latex]x=0[/latex] trivijalno provjerimo da [latex]f[/latex] zadovoljava uvjete zadatka), kao i da je [latex]\cot(\mathrm{arccot} x)=x[/latex].
Dakle, imamo [latex]\cot f(x)=\displaystyle\frac{\displaystyle\frac{x}{x}-1}{x+\displaystyle\frac{1}{x}}[/latex]. (Primjećujemo da nazivnik nije nikad jednak [latex]0[/latex].) Dakle, [latex]\cot f(x)=0[/latex], pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za [latex]x\neq 0[/latex], ali za [latex]x=0[/latex] dobivamo odgovor direktnim uvrštavanjem.)
Eto, nije baš toliko teško koliko mi se činilo pred dvije godine. :D Ali dobro, ta ideja... možda malkice čudna, da. :)
Dobro, znam da su kolokviji prošli, ali nije to valjda razlog da vas prestanu zanimati rješenja zadataka? 
Uglavnom, da, nije baš najtrivijalniji zadatak (barem ovako, bez derivacija), sjećam ga se još iz doba ( ) dok sam ja bio na prvoj godini. ) dok sam ja bio na prvoj godini.  Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju. Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju.
No, ajde da vidimo. Neka je 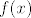 funkcija s lijeve strane jednadžbe. Očito vrijedi funkcija s lijeve strane jednadžbe. Očito vrijedi 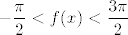 . To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi . To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi 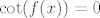 , imat ćemo da je , imat ćemo da je 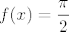 . (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo . (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo  .) .)
No dobro, ajde. Dakle, kotangensujmo to i sad idemo po adicijskim formulama za kotangens. Njih se da izvesti, a i relativno su poznate. Dakle, imamo 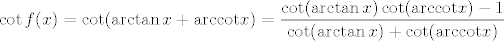 . Sad koristimo da je . Sad koristimo da je 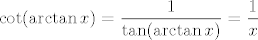 (pri čemu to ima smisla samo za (pri čemu to ima smisla samo za 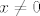 , ali za , ali za  trivijalno provjerimo da trivijalno provjerimo da  zadovoljava uvjete zadatka), kao i da je zadovoljava uvjete zadatka), kao i da je 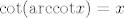 . .
Dakle, imamo 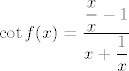 . (Primjećujemo da nazivnik nije nikad jednak . (Primjećujemo da nazivnik nije nikad jednak  .) Dakle, .) Dakle, 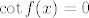 , pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za , pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za 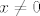 , ali za , ali za  dobivamo odgovor direktnim uvrštavanjem.) dobivamo odgovor direktnim uvrštavanjem.)
Eto, nije baš toliko teško koliko mi se činilo pred dvije godine.  Ali dobro, ta ideja... možda malkice čudna, da. Ali dobro, ta ideja... možda malkice čudna, da. 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
 Postano: 21:10 pon, 25. 10. 2010 Naslov: Postano: 21:10 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="mornik"]Dobro, znam da su kolokviji prošli, [u]ali nije to valjda razlog da vas prestanu zanimati rješenja zadataka[/u]? :P
Uglavnom, da, nije baš najtrivijalniji zadatak (barem ovako, bez derivacija), sjećam ga se još iz doba (:djed:) dok sam ja bio na prvoj godini. :) Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju.
No, ajde da vidimo. Neka je [latex]f(x)[/latex] funkcija s lijeve strane jednadžbe. Očito vrijedi [latex]-\displaystyle\frac{\pi}{2}<f(x)<\displaystyle\frac{3\pi}{2}[/latex]. To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi [latex]\cot (f(x))=0[/latex], imat ćemo da je [latex]f(x)=\displaystyle\frac{\pi}{2}[/latex]. (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo [latex]\displaystyle\frac{\pi}{2}[/latex].)
No dobro, ajde. Dakle, kotangensujmo to i sad idemo po adicijskim formulama za kotangens. Njih se da izvesti, a i relativno su poznate. Dakle, imamo [latex]\cot f(x)=\cot (\arctan x+\mathrm{arccot} x)=\displaystyle\frac{\cot (\arctan x)\cot(\mathrm{arccot} x)-1}{\cot (\arctan x)+\cot(\mathrm{arccot} x)}[/latex]. Sad koristimo da je [latex]\cot(\arctan x)=\displaystyle\frac{1}{\tan(\arctan x)}=\displaystyle\frac{1}{x}[/latex] (pri čemu to ima smisla samo za [latex]x\neq 0[/latex], ali za [latex]x=0[/latex] trivijalno provjerimo da [latex]f[/latex] zadovoljava uvjete zadatka), kao i da je [latex]\cot(\mathrm{arccot} x)=x[/latex].
Dakle, imamo [latex]\cot f(x)=\displaystyle\frac{\displaystyle\frac{x}{x}-1}{x+\displaystyle\frac{1}{x}}[/latex]. (Primjećujemo da nazivnik nije nikad jednak [latex]0[/latex].) Dakle, [latex]\cot f(x)=0[/latex], pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za [latex]x\neq 0[/latex], ali za [latex]x=0[/latex] dobivamo odgovor direktnim uvrštavanjem.)
Eto, nije baš toliko teško koliko mi se činilo pred dvije godine. :D Ali dobro, ta ideja... možda malkice čudna, da. :)[/quote]
| mornik (napisa): | Dobro, znam da su kolokviji prošli, ali nije to valjda razlog da vas prestanu zanimati rješenja zadataka? 
Uglavnom, da, nije baš najtrivijalniji zadatak (barem ovako, bez derivacija), sjećam ga se još iz doba ( ) dok sam ja bio na prvoj godini. ) dok sam ja bio na prvoj godini.  Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju. Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju.
No, ajde da vidimo. Neka je 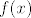 funkcija s lijeve strane jednadžbe. Očito vrijedi funkcija s lijeve strane jednadžbe. Očito vrijedi 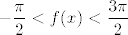 . To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi . To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi 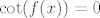 , imat ćemo da je , imat ćemo da je 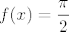 . (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo . (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo  .) .)
No dobro, ajde. Dakle, kotangensujmo to i sad idemo po adicijskim formulama za kotangens. Njih se da izvesti, a i relativno su poznate. Dakle, imamo 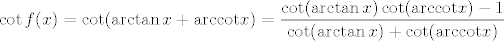 . Sad koristimo da je . Sad koristimo da je 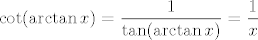 (pri čemu to ima smisla samo za (pri čemu to ima smisla samo za 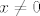 , ali za , ali za  trivijalno provjerimo da trivijalno provjerimo da  zadovoljava uvjete zadatka), kao i da je zadovoljava uvjete zadatka), kao i da je 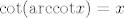 . .
Dakle, imamo 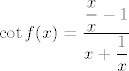 . (Primjećujemo da nazivnik nije nikad jednak . (Primjećujemo da nazivnik nije nikad jednak  .) Dakle, .) Dakle, 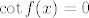 , pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za , pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za 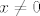 , ali za , ali za  dobivamo odgovor direktnim uvrštavanjem.) dobivamo odgovor direktnim uvrštavanjem.)
Eto, nije baš toliko teško koliko mi se činilo pred dvije godine.  Ali dobro, ta ideja... možda malkice čudna, da. Ali dobro, ta ideja... možda malkice čudna, da.  |
Zadnja promjena: Lanek_; 6:29 uto, 26. 10. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
 Postano: 21:20 pon, 25. 10. 2010 Naslov: Postano: 21:20 pon, 25. 10. 2010 Naslov: |
    |
|
|
[quote="mornik"]Dobro, znam da su kolokviji prošli, ali nije to valjda razlog da vas prestanu zanimati rješenja zadataka? :P
Uglavnom, da, nije baš najtrivijalniji zadatak (barem ovako, bez derivacija), sjećam ga se još iz doba (:djed:) dok sam ja bio na prvoj godini. :) Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju.
No, ajde da vidimo. Neka je [latex]f(x)[/latex] funkcija s lijeve strane jednadžbe. Očito vrijedi [latex]-\displaystyle\frac{\pi}{2}<f(x)<\displaystyle\frac{3\pi}{2}[/latex]. To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi [latex]\cot (f(x))=0[/latex], imat ćemo da je [latex]f(x)=\displaystyle\frac{\pi}{2}[/latex]. (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo [latex]\displaystyle\frac{\pi}{2}[/latex].)
No dobro, ajde. Dakle, kotangensujmo to i sad idemo po adicijskim formulama za kotangens. Njih se da izvesti, a i relativno su poznate. Dakle, imamo [latex]\cot f(x)=\cot (\arctan x+\mathrm{arccot} x)=\displaystyle\frac{\cot (\arctan x)\cot(\mathrm{arccot} x)-1}{\cot (\arctan x)+\cot(\mathrm{arccot} x)}[/latex]. Sad koristimo da je [latex]\cot(\arctan x)=\displaystyle\frac{1}{\tan(\arctan x)}=\displaystyle\frac{1}{x}[/latex] (pri čemu to ima smisla samo za [latex]x\neq 0[/latex], ali za [latex]x=0[/latex] trivijalno provjerimo da [latex]f[/latex] zadovoljava uvjete zadatka), kao i da je [latex]\cot(\mathrm{arccot} x)=x[/latex].
Dakle, imamo [latex]\cot f(x)=\displaystyle\frac{\displaystyle\frac{x}{x}-1}{x+\displaystyle\frac{1}{x}}[/latex]. (Primjećujemo da nazivnik nije nikad jednak [latex]0[/latex].) Dakle, [latex]\cot f(x)=0[/latex], pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za [latex]x\neq 0[/latex], ali za [latex]x=0[/latex] dobivamo odgovor direktnim uvrštavanjem.)
Eto, nije baš toliko teško koliko mi se činilo pred dvije godine. :D Ali dobro, ta ideja... možda malkice čudna, da. :)[/quote]
kad si radio zadatke iz domaćeg onda ( a to je jedan od njih ) prije 2 godine, reko si da se to pomnoži s arcctg i tamo da dobijemo nulu sa strane. smijemo li to raditi ( s obzirom na pravilo da 'ne diramo desnu stranu' kod dokaza) pa eto, učinilo se zgodno pa da pitam :)
P.S.: jel ispo dobro onaj integral s vodom na kraju ? :P
| mornik (napisa): | Dobro, znam da su kolokviji prošli, ali nije to valjda razlog da vas prestanu zanimati rješenja zadataka? 
Uglavnom, da, nije baš najtrivijalniji zadatak (barem ovako, bez derivacija), sjećam ga se još iz doba ( ) dok sam ja bio na prvoj godini. ) dok sam ja bio na prvoj godini.  Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju. Mislim, nije nešto težak, samo ima tu jednu relativno netipičnu ideju.
No, ajde da vidimo. Neka je 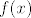 funkcija s lijeve strane jednadžbe. Očito vrijedi funkcija s lijeve strane jednadžbe. Očito vrijedi 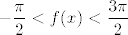 . To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi . To čisto slijedi iz slika tih dvaju arkusa. Dakle, ukoliko mi pokažemo da vrijedi 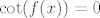 , imat ćemo da je , imat ćemo da je 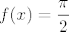 . (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo . (To vrijedi zato što je jedina nultočka kotangensa na intervalu koji gore spominjemo upravo  .) .)
No dobro, ajde. Dakle, kotangensujmo to i sad idemo po adicijskim formulama za kotangens. Njih se da izvesti, a i relativno su poznate. Dakle, imamo 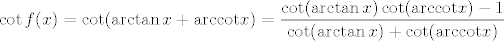 . Sad koristimo da je . Sad koristimo da je 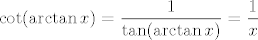 (pri čemu to ima smisla samo za (pri čemu to ima smisla samo za 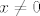 , ali za , ali za  trivijalno provjerimo da trivijalno provjerimo da  zadovoljava uvjete zadatka), kao i da je zadovoljava uvjete zadatka), kao i da je 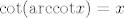 . .
Dakle, imamo 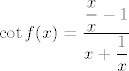 . (Primjećujemo da nazivnik nije nikad jednak . (Primjećujemo da nazivnik nije nikad jednak  .) Dakle, .) Dakle, 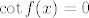 , pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za , pa smo dokazali našu tvrdnju. (Još jednom ponavljam, ako se ne varam, ovaj zadnji odlomak vrijedi samo za 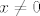 , ali za , ali za  dobivamo odgovor direktnim uvrštavanjem.) dobivamo odgovor direktnim uvrštavanjem.)
Eto, nije baš toliko teško koliko mi se činilo pred dvije godine.  Ali dobro, ta ideja... možda malkice čudna, da. Ali dobro, ta ideja... možda malkice čudna, da.  |
kad si radio zadatke iz domaćeg onda ( a to je jedan od njih ) prije 2 godine, reko si da se to pomnoži s arcctg i tamo da dobijemo nulu sa strane. smijemo li to raditi ( s obzirom na pravilo da 'ne diramo desnu stranu' kod dokaza) pa eto, učinilo se zgodno pa da pitam 
P.S.: jel ispo dobro onaj integral s vodom na kraju ? 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 5:02 uto, 26. 10. 2010 Naslov: Postano: 5:02 uto, 26. 10. 2010 Naslov: |
    |
|
|
Hvala na pitanju, integral je možda čak i prošao malo bolje koliko sam očekivao kad sam ga vidio. :)
U vezi tvojeg prvog pitanja, ne znam misliš li na ovaj zadatak ili na neki drugi (jer kažeš da nešto množimo s arkus kotangensom, a tu ništa ne množim :? ), ali u svakom slučaju, nisam upoznat s pravilom "ne diramo desnu stranu kod dokaza". :) Da malo apstraktnije objasnim dokaz, ja sam tvrdnju gore dokazao tako da sam našao njoj ekvivalentnu tvrdnju, dokazao da je ekvivalentna originalnoj i dokazao da ta ekvivalentna tvrdnja vrijedi, i to je sasvim legalno, kad razmislimo. Sad, ne znam kako misliš da ne diramo desnu stranu prilikom dokaza - svaki dokaz je u redu ako i samo ako legalno dokazuje tvrdnju (dakle, ako u njemu ne činimo ništa nedopušteno i moralno dvojbeno :)). Na primjer, u dokazu (trivijalnom, ali nema veze) da iz [latex]x^2=y^2[/latex] slijedi [latex]|x|=|y|[/latex] mi diramo desnu stranu - recimo, ako "prebacujemo [latex]y^2[/latex] na lijevu stranu" (što bi reklo da zapravo oduzimamo [latex]y^2[/latex] s obje strane, što je sasvim dopušten potez) i tako dobivamo [latex](x-y)(x+y)=0[/latex], to je opet diranje desne strane. Tako da ne znam baš o čemu se radi... :P
Hvala na pitanju, integral je možda čak i prošao malo bolje koliko sam očekivao kad sam ga vidio. 
U vezi tvojeg prvog pitanja, ne znam misliš li na ovaj zadatak ili na neki drugi (jer kažeš da nešto množimo s arkus kotangensom, a tu ništa ne množim  ), ali u svakom slučaju, nisam upoznat s pravilom "ne diramo desnu stranu kod dokaza". ), ali u svakom slučaju, nisam upoznat s pravilom "ne diramo desnu stranu kod dokaza".  Da malo apstraktnije objasnim dokaz, ja sam tvrdnju gore dokazao tako da sam našao njoj ekvivalentnu tvrdnju, dokazao da je ekvivalentna originalnoj i dokazao da ta ekvivalentna tvrdnja vrijedi, i to je sasvim legalno, kad razmislimo. Sad, ne znam kako misliš da ne diramo desnu stranu prilikom dokaza - svaki dokaz je u redu ako i samo ako legalno dokazuje tvrdnju (dakle, ako u njemu ne činimo ništa nedopušteno i moralno dvojbeno Da malo apstraktnije objasnim dokaz, ja sam tvrdnju gore dokazao tako da sam našao njoj ekvivalentnu tvrdnju, dokazao da je ekvivalentna originalnoj i dokazao da ta ekvivalentna tvrdnja vrijedi, i to je sasvim legalno, kad razmislimo. Sad, ne znam kako misliš da ne diramo desnu stranu prilikom dokaza - svaki dokaz je u redu ako i samo ako legalno dokazuje tvrdnju (dakle, ako u njemu ne činimo ništa nedopušteno i moralno dvojbeno  ). Na primjer, u dokazu (trivijalnom, ali nema veze) da iz ). Na primjer, u dokazu (trivijalnom, ali nema veze) da iz  slijedi slijedi 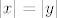 mi diramo desnu stranu - recimo, ako "prebacujemo mi diramo desnu stranu - recimo, ako "prebacujemo 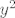 na lijevu stranu" (što bi reklo da zapravo oduzimamo na lijevu stranu" (što bi reklo da zapravo oduzimamo 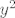 s obje strane, što je sasvim dopušten potez) i tako dobivamo s obje strane, što je sasvim dopušten potez) i tako dobivamo 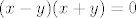 , to je opet diranje desne strane. Tako da ne znam baš o čemu se radi... , to je opet diranje desne strane. Tako da ne znam baš o čemu se radi... 
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
 Postano: 12:47 sri, 27. 10. 2010 Naslov: Postano: 12:47 sri, 27. 10. 2010 Naslov: |
    |
|
|
[quote="mornik"]Hvala na pitanju, integral je možda čak i prošao malo bolje koliko sam očekivao kad sam ga vidio. :)
U vezi tvojeg prvog pitanja, ne znam misliš li na ovaj zadatak ili na neki drugi (jer kažeš da nešto množimo s arkus kotangensom, a tu ništa ne množim :? ), ali u svakom slučaju, nisam upoznat s pravilom "ne diramo desnu stranu kod dokaza". :) Da malo apstraktnije objasnim dokaz, ja sam tvrdnju gore dokazao tako da sam našao njoj ekvivalentnu tvrdnju, dokazao da je ekvivalentna originalnoj i dokazao da ta ekvivalentna tvrdnja vrijedi, i to je sasvim legalno, kad razmislimo. Sad, ne znam kako misliš da ne diramo desnu stranu prilikom dokaza - svaki dokaz je u redu ako i samo ako legalno dokazuje tvrdnju (dakle, ako u njemu ne činimo ništa nedopušteno i moralno dvojbeno :)). Na primjer, u dokazu (trivijalnom, ali nema veze) da iz [latex]x^2=y^2[/latex] slijedi [latex]|x|=|y|[/latex] mi diramo desnu stranu - recimo, ako "prebacujemo [latex]y^2[/latex] na lijevu stranu" (što bi reklo da zapravo oduzimamo [latex]y^2[/latex] s obje strane, što je sasvim dopušten potez) i tako dobivamo [latex](x-y)(x+y)=0[/latex], to je opet diranje desne strane. Tako da ne znam baš o čemu se radi... :P[/quote]
dobro, djeluješ s ctg, ne množiš, ajde :) ( zadatak je inače odavde - http://degiorgi.math.hr/forum/viewtopic.php?t=13930 )
samo me zanimalo jer recimo kod indukcije ne smiješ 'dirati desnu stranu' nego pretpostaviš jedno i to svodiš na ekvivalentnu tvrdnju onoj što stoji iza znaka implikacije...recimo :D
al relativno glupo pitanje je bilo..svejedno hvala i moj grijeh :oops:
| mornik (napisa): | Hvala na pitanju, integral je možda čak i prošao malo bolje koliko sam očekivao kad sam ga vidio. 
U vezi tvojeg prvog pitanja, ne znam misliš li na ovaj zadatak ili na neki drugi (jer kažeš da nešto množimo s arkus kotangensom, a tu ništa ne množim  ), ali u svakom slučaju, nisam upoznat s pravilom "ne diramo desnu stranu kod dokaza". ), ali u svakom slučaju, nisam upoznat s pravilom "ne diramo desnu stranu kod dokaza".  Da malo apstraktnije objasnim dokaz, ja sam tvrdnju gore dokazao tako da sam našao njoj ekvivalentnu tvrdnju, dokazao da je ekvivalentna originalnoj i dokazao da ta ekvivalentna tvrdnja vrijedi, i to je sasvim legalno, kad razmislimo. Sad, ne znam kako misliš da ne diramo desnu stranu prilikom dokaza - svaki dokaz je u redu ako i samo ako legalno dokazuje tvrdnju (dakle, ako u njemu ne činimo ništa nedopušteno i moralno dvojbeno Da malo apstraktnije objasnim dokaz, ja sam tvrdnju gore dokazao tako da sam našao njoj ekvivalentnu tvrdnju, dokazao da je ekvivalentna originalnoj i dokazao da ta ekvivalentna tvrdnja vrijedi, i to je sasvim legalno, kad razmislimo. Sad, ne znam kako misliš da ne diramo desnu stranu prilikom dokaza - svaki dokaz je u redu ako i samo ako legalno dokazuje tvrdnju (dakle, ako u njemu ne činimo ništa nedopušteno i moralno dvojbeno  ). Na primjer, u dokazu (trivijalnom, ali nema veze) da iz ). Na primjer, u dokazu (trivijalnom, ali nema veze) da iz  slijedi slijedi 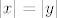 mi diramo desnu stranu - recimo, ako "prebacujemo mi diramo desnu stranu - recimo, ako "prebacujemo 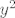 na lijevu stranu" (što bi reklo da zapravo oduzimamo na lijevu stranu" (što bi reklo da zapravo oduzimamo 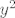 s obje strane, što je sasvim dopušten potez) i tako dobivamo s obje strane, što je sasvim dopušten potez) i tako dobivamo 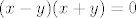 , to je opet diranje desne strane. Tako da ne znam baš o čemu se radi... , to je opet diranje desne strane. Tako da ne znam baš o čemu se radi...  |
dobro, djeluješ s ctg, ne množiš, ajde  ( zadatak je inače odavde - http://degiorgi.math.hr/forum/viewtopic.php?t=13930 ) ( zadatak je inače odavde - http://degiorgi.math.hr/forum/viewtopic.php?t=13930 )
samo me zanimalo jer recimo kod indukcije ne smiješ 'dirati desnu stranu' nego pretpostaviš jedno i to svodiš na ekvivalentnu tvrdnju onoj što stoji iza znaka implikacije...recimo 
al relativno glupo pitanje je bilo..svejedno hvala i moj grijeh 
|
|
| [Vrh] |
|
|





