| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mata2706
Forumaš(ica)

Pridružen/a: 31. 10. 2010. (19:17:39)
Postovi: (2)16
Lokacija: Sisak
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:10 ned, 31. 10. 2010 Naslov: Postano: 22:10 ned, 31. 10. 2010 Naslov: |
    |
|
|
Idem ja rješavati nejednadžbu da malo vježbam LaTex...
[latex]p^2-(4p)(p-1)\geq 0[/latex]
[latex]p^2-4p^2+4p\geq 0[/latex]
[latex]-3p^2+4p\geq 0[/latex]
Odredimo sada nultočke parabole:
[latex]p_{1,2}=\frac{-4 \pm\sqrt {4^2-4*(-3)*0}} {-6}[/latex]
[latex]p_{1,2}=\frac{-4 \pm 4} {-6}[/latex]
dakle su nultočke [latex]x_1 =0, x_2=\frac{4} {3}[/latex]
Kako je [latex]a<0 \ tj. \ a=-3[/latex] parabola ima "kapu" prema gore, tj. ona ima svoj maksimum u tjemenu. Kako je u danoj nejednadžbi znak [latex]\geq[/latex], i nultočke pripadaju intervalu pa je skup rješenja nejednadžbe [latex]p\in [0, \frac {4} {3}][/latex]
Evo, nadam se da je sve dobro! Inače, ja sam 4. raz. opće gimnazije i jedva čekam da dođem na vaš faks :)
(Ovo je sad ispravljeno, Goranm me ispravio)
Idem ja rješavati nejednadžbu da malo vježbam LaTex...
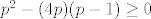
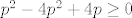
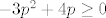
Odredimo sada nultočke parabole:
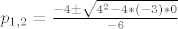
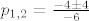
dakle su nultočke 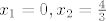
Kako je 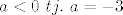 parabola ima "kapu" prema gore, tj. ona ima svoj maksimum u tjemenu. Kako je u danoj nejednadžbi znak parabola ima "kapu" prema gore, tj. ona ima svoj maksimum u tjemenu. Kako je u danoj nejednadžbi znak 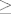 , i nultočke pripadaju intervalu pa je skup rješenja nejednadžbe , i nultočke pripadaju intervalu pa je skup rješenja nejednadžbe 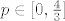
Evo, nadam se da je sve dobro! Inače, ja sam 4. raz. opće gimnazije i jedva čekam da dođem na vaš faks 
(Ovo je sad ispravljeno, Goranm me ispravio)
_________________
U matematici se sve smije, osim pogriješiti!
Zadnja promjena: Vishykc; 22:52 ned, 31. 10. 2010; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:24 ned, 31. 10. 2010 Naslov: Postano: 23:24 ned, 31. 10. 2010 Naslov: |
    |
|
|
[quote="goranm"][quote="Vishykc"]skup rješenja nejednadžbe [je] [latex]p\in [0, \frac {4} {3}][/latex][/quote]
Treba se još uočiti da za [bg=green]jedan[/bg][latex]p\in [0, \frac {4} {3}][/latex] početna jednadžba nije zadovoljena. ;)[/quote]
Aha, to bi bio 0. (Skoro sam napisal 0! kao usklična reč., a to ne bi bilo dobro :D). A gdje se to desilo da je to rješenje ušlo u skup? Znači da nejednadžba [latex]p^2-(4p)(p-1)\geq 0 [/latex] nije ekvivalentna onoj koja bi trebala biti da skup rješenja bude potpuno točan? Uf, jesam skompliciral pitanje...
| goranm (napisa): | | Vishykc (napisa): | skup rješenja nejednadžbe [je] 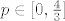 |
Treba se još uočiti da za jedan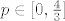 početna jednadžba nije zadovoljena. početna jednadžba nije zadovoljena.  |
Aha, to bi bio 0. (Skoro sam napisal 0! kao usklična reč., a to ne bi bilo dobro  ). A gdje se to desilo da je to rješenje ušlo u skup? Znači da nejednadžba ). A gdje se to desilo da je to rješenje ušlo u skup? Znači da nejednadžba 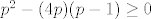 nije ekvivalentna onoj koja bi trebala biti da skup rješenja bude potpuno točan? Uf, jesam skompliciral pitanje... nije ekvivalentna onoj koja bi trebala biti da skup rješenja bude potpuno točan? Uf, jesam skompliciral pitanje...
_________________
U matematici se sve smije, osim pogriješiti!
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
 Postano: 23:37 ned, 31. 10. 2010 Naslov: Postano: 23:37 ned, 31. 10. 2010 Naslov: |
    |
|
|
[quote="Vishykc"][quote="goranm"][quote="Vishykc"]skup rješenja nejednadžbe [je] [latex]p\in [0, \frac {4} {3}][/latex][/quote]
Treba se još uočiti da za [bg=green]jedan[/bg][latex]p\in [0, \frac {4} {3}][/latex] početna jednadžba nije zadovoljena. ;)[/quote]
Aha, to bi bio 0. (Skoro sam napisal 0! kao usklična reč., a to ne bi bilo dobro :D). A gdje se to desilo da je to rješenje ušlo u skup? Znači da nejednadžba [latex]p^2-(4p)(p-1)\geq 0 [/latex] nije ekvivalentna onoj koja bi trebala biti da skup rješenja bude potpuno točan? Uf, jesam skompliciral pitanje...[/quote]
Sjeti se formule za rješavanje kvadratne jednadžbe i njezinog nazivnika. :) entuzijastičnom poput tebe to bi trebalo bit i previše hintova :P
| Vishykc (napisa): | | goranm (napisa): | | Vishykc (napisa): | skup rješenja nejednadžbe [je] 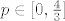 |
Treba se još uočiti da za jedan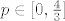 početna jednadžba nije zadovoljena. početna jednadžba nije zadovoljena.  |
Aha, to bi bio 0. (Skoro sam napisal 0! kao usklična reč., a to ne bi bilo dobro  ). A gdje se to desilo da je to rješenje ušlo u skup? Znači da nejednadžba ). A gdje se to desilo da je to rješenje ušlo u skup? Znači da nejednadžba 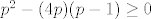 nije ekvivalentna onoj koja bi trebala biti da skup rješenja bude potpuno točan? Uf, jesam skompliciral pitanje... nije ekvivalentna onoj koja bi trebala biti da skup rješenja bude potpuno točan? Uf, jesam skompliciral pitanje... |
Sjeti se formule za rješavanje kvadratne jednadžbe i njezinog nazivnika.  entuzijastičnom poput tebe to bi trebalo bit i previše hintova entuzijastičnom poput tebe to bi trebalo bit i previše hintova 
_________________
No, you clearly don’t know who you’re talking to, so let me clue you in: I am not in danger, Skylar. I am the danger. A guy opens his door and gets shot and you think that of me? No. I am the one who knocks.
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:08 pon, 1. 11. 2010 Naslov: Postano: 0:08 pon, 1. 11. 2010 Naslov: |
    |
|
|
Da, možda i previše :oops: ...Al štel sam videt kak to pravi matematičari stručno kažu... [latex]x_1=0[/latex] slijedi da je [latex]0=\frac {-b+ \sqrt {b^2-4ac}}{2a}[/latex] tj, [latex]-b+ \sqrt{b^2-4ac}=0[/latex]. Kako je a različito od 0 (jer inače ne bi bila kvadratna jednadžba), slijedi da je c=0, a u početnoj jednadžbi c nije 0, tj. morao bi p biti 1 i 0 istovremeno, što je kontradikcija?
Da, možda i previše  ...Al štel sam videt kak to pravi matematičari stručno kažu... ...Al štel sam videt kak to pravi matematičari stručno kažu... 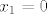 slijedi da je slijedi da je 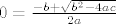 tj, tj,  . Kako je a različito od 0 (jer inače ne bi bila kvadratna jednadžba), slijedi da je c=0, a u početnoj jednadžbi c nije 0, tj. morao bi p biti 1 i 0 istovremeno, što je kontradikcija? . Kako je a različito od 0 (jer inače ne bi bila kvadratna jednadžba), slijedi da je c=0, a u početnoj jednadžbi c nije 0, tj. morao bi p biti 1 i 0 istovremeno, što je kontradikcija?
_________________
U matematici se sve smije, osim pogriješiti!
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:25 pon, 1. 11. 2010 Naslov: Postano: 12:25 pon, 1. 11. 2010 Naslov: |
    |
|
|
Da, dok se početna jednadžba sredi je "p" zapravo "a" kvadratne jednadžbe, što je razl. od 0... Nisam mislil da je tak lagano, pa sam kompliciral... Evo, napokon smo zajedničkim snagama svi zajedno uspjeli rješiti "dječju" kvadratnu nejednadžbu :D.
Da, dok se početna jednadžba sredi je "p" zapravo "a" kvadratne jednadžbe, što je razl. od 0... Nisam mislil da je tak lagano, pa sam kompliciral... Evo, napokon smo zajedničkim snagama svi zajedno uspjeli rješiti "dječju" kvadratnu nejednadžbu  . .
_________________
U matematici se sve smije, osim pogriješiti!
|
|
| [Vrh] |
|
|















