|
Označili smo s [latex]a_1, a_2, a_3[/latex] elemente dane baze za [latex]M[/latex], a s [latex]b_1, b_2, b_3[/latex] elemente druge baze.
Dobi se [latex]b_1 = -2 a_2 + a_3[/latex] (mislim da sam ovo krivo rješio na demonstraturama, ne može se dobiti višestruko rješenje) i [latex]b_3 = 3 a_3 - b_1[/latex] ([latex]b_2[/latex] se ne može prikazati preko prethodnika). U bazu za presjek stavljamo samo dio s a-ovima. Za [latex]b_1[/latex] to je [latex]-2 a_2 + a_3[/latex], što je zapravo jednako [latex]b_1[/latex], pa da si skratimo pisanje, napišemo da je on u bazi. Iz [latex]b_3[/latex] uzmemo [latex]3 a_3[/latex]. Na kolokoviju bi bilo pristojno napisati što je baza bez korištenja oznaka. Ovdje, to je [latex]\{ (1, -1, 1, -1), (3, 3, 3, 3) \}[/latex].
[quote="mayam"]i jos nesto zasto ne vrijde one formule za dim..i kada one vrijede[/quote]
Vrijede uvijek, pa tako i ovdje. Dimenzija od [latex]M[/latex] i [latex]L[/latex] je 3, dobili smo da je dimenzija sume 4 (dobili smo gornjim postupkom da je [latex]\{ a_1, a_2, a_3, b_2 \}[/latex] baza za sumu), a od presjeka 2. Vrijedi [latex]3 + 3 = 4 + 2[/latex].
[quote="mayam"]dim(S+L)= dimS= dimL[/quote]
To vrijedi ako i samo ako je S=L.
Označili smo s 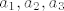 elemente dane baze za elemente dane baze za  , a s , a s 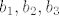 elemente druge baze. elemente druge baze.
Dobi se 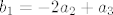 (mislim da sam ovo krivo rješio na demonstraturama, ne može se dobiti višestruko rješenje) i (mislim da sam ovo krivo rješio na demonstraturama, ne može se dobiti višestruko rješenje) i 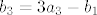 ( (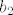 se ne može prikazati preko prethodnika). U bazu za presjek stavljamo samo dio s a-ovima. Za se ne može prikazati preko prethodnika). U bazu za presjek stavljamo samo dio s a-ovima. Za 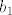 to je to je 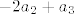 , što je zapravo jednako , što je zapravo jednako 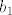 , pa da si skratimo pisanje, napišemo da je on u bazi. Iz , pa da si skratimo pisanje, napišemo da je on u bazi. Iz 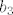 uzmemo uzmemo 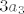 . Na kolokoviju bi bilo pristojno napisati što je baza bez korištenja oznaka. Ovdje, to je . Na kolokoviju bi bilo pristojno napisati što je baza bez korištenja oznaka. Ovdje, to je 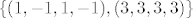 . .
| mayam (napisa): | | i jos nesto zasto ne vrijde one formule za dim..i kada one vrijede |
Vrijede uvijek, pa tako i ovdje. Dimenzija od  i i  je 3, dobili smo da je dimenzija sume 4 (dobili smo gornjim postupkom da je je 3, dobili smo da je dimenzija sume 4 (dobili smo gornjim postupkom da je 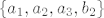 baza za sumu), a od presjeka 2. Vrijedi baza za sumu), a od presjeka 2. Vrijedi 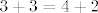 . .
| mayam (napisa): | | dim(S+L)= dimS= dimL |
To vrijedi ako i samo ako je S=L.
|





