|
Uffff, počnimo! :D
Imamo dva niza slučajnih varijabli, [latex]A=\left(A_n\right)_{n \in \mathbb{N}_0}[/latex], [latex]B=\left(B_n\right)_{n \in \mathbb{N}_0}[/latex]. [latex]A_n[/latex] nam je broj [b]zlatnih[/b] krijesnica u trenutku [latex]n[/latex], a [latex]B_n[/latex] broj [b]zelenih[/b]. Zanima nas koliko je [latex]\mathds{E}\left(A_n\right)[/latex], za svaki [latex]n \in \mathbb{N}[/latex], uz uvjet da je [latex]A_0=0[/latex] i [latex]B_0=1[/latex].
Neka je [latex]n \in \mathbb{N}[/latex], primjetimo da vrijedi
[latex]A_{n+1} = 2 \cdot A_{n} + 3 \cdot B_{n} - B_{n+1}[/latex].
Naime, u svakom koraku se broj zlatnih poveća, a od zelenih može nastati najviše trostruko toliko zlatnih, ali onda još od toga oduzmemo koliko je zelenih nastalo, nadam se da je jasno... :)
Sada ovu rekurziju "napadnemo" očekivanjem i iskoristimo linearnost istoga. Dobivamo
[latex]\mathds{E}\left(A_{n+1}\right) = 2 \cdot \mathds{E}\left(A_{n}\right) + 3 \cdot \mathds{E}\left(B_{n}\right) - \mathds{E}\left(B_{n+1}\right)[/latex].
Uvedimo oznake [latex]a_n := \mathds{E}\left(A_n\right),\, b_n := \mathds{E}\left(B_n\right);\ n \in \mathbb{N}[/latex].
Nadalje, primjetimo da je [latex]B[/latex] jednostavan proces grananja, gdje je
[latex]B_1 \sim \left(\begin{array}{cccc}
0 & 1 & 2 & 3 \\
\frac{1}{8} & \frac{3}{8} & \frac{3}{8} & \frac{1}{8}
\end{array}\right)[/latex].
Zanima nas samo koliko svaka zelena krijesnica daje zelenih krijesnica, zlatne krijesnice ne utječu na broj zelenih krijesnica.
Sada možemo izračunati koliko je [latex]b_n[/latex]. Vrijedi
[latex]P\left(s\right) := P_{B_1}\left(s\right) = \left[\frac{1}{2}\left(1+s\right)\right]^3[/latex],
također je [latex]P_{B_n}\left(s\right)=\underbrace{P \circ P \circ \ldots \circ P}_{n}\left(s\right) =: P_n\left(s\right)[/latex]. U ovom se trenutku prisjetimo da je [latex]P\left(1\right)=1[/latex], što nam induktivno povlači da je [latex]P_n\left(1\right)=1[/latex], za svaki [latex]n \in \mathbb{N}[/latex].
Konačno je [latex]b_n = \lim\limits_{s \nearrow 1}{P'_n\left(s\right)}=P'_n\left(1\right) = P'\left[P_{n-1}\left(1\right)\right] \cdot P'_{n-1}\left(1\right) =[/latex]
[latex]=P'\left(1\right) \cdot P'_{n-1}\left(1\right) = \ldots = \left[P'\left(1\right)\right]^{n}=\left(\frac{3}{2}\right)^n[/latex]. Druga jednakost vrijedi jer je prva derivacija dobro definirana u točki [latex]s=1[/latex].
Dakle, trebamo rješiti rekurziju
[latex]a_{n+1}-2a_{n} = 3 \cdot \left(\frac{3}{2}\right)^{n} - \left(\frac{3}{2}\right)^{n+1} = \left(\frac{3}{2}\right)^{n+1}[/latex].
Rješenje pripadajuće homogene jednadžbe [latex]\left(a_{n+1} - 2a_{n}=0\right)[/latex] je očito [latex]a_n^H = A \cdot 2^n,\, n \in \mathbb{N}[/latex], za neku konstantu [latex]A>0[/latex]. Iz oblika na desnoj strani rekurzije znamo da je partikularno rješenje oblika [latex]a_n^P = B \cdot \left(\frac{3}{2}\right)^n,\, n \in \mathbb{N}[/latex], za neku konstantu [latex]B>0[/latex].
Dakle, rješenje ima oblik [latex]a_n = A \cdot 2^n + B \dot \left(\frac{3}{2}\right)^n;\ n \in \mathbb{N},\, A>0,\, B>0[/latex].
[latex]a_1=\frac{3}{2}[/latex] i [latex]a_2=\frac{21}{4}[/latex] računamo na prste te nalazimo da je [latex]A=3[/latex] i [latex]B=-3[/latex].
Konačno je
[latex]\mathds{E}\left(A_n\right)=3 \cdot \left[2^n - \left(\frac{3}{2}\right)^n\right],\, n \in \mathbb{N}[/latex].
Uffff, počnimo! 
Imamo dva niza slučajnih varijabli, 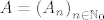 , , 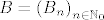 . . 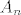 nam je broj zlatnih krijesnica u trenutku nam je broj zlatnih krijesnica u trenutku  , a , a 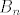 broj zelenih. Zanima nas koliko je broj zelenih. Zanima nas koliko je 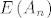 , za svaki , za svaki  , uz uvjet da je , uz uvjet da je 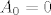 i i 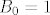 . .
Neka je  , primjetimo da vrijedi , primjetimo da vrijedi
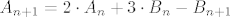 . .
Naime, u svakom koraku se broj zlatnih poveća, a od zelenih može nastati najviše trostruko toliko zlatnih, ali onda još od toga oduzmemo koliko je zelenih nastalo, nadam se da je jasno... 
Sada ovu rekurziju "napadnemo" očekivanjem i iskoristimo linearnost istoga. Dobivamo
 . .
Uvedimo oznake 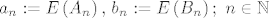 . .
Nadalje, primjetimo da je  jednostavan proces grananja, gdje je jednostavan proces grananja, gdje je
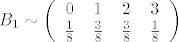 . .
Zanima nas samo koliko svaka zelena krijesnica daje zelenih krijesnica, zlatne krijesnice ne utječu na broj zelenih krijesnica.
Sada možemo izračunati koliko je 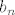 . Vrijedi . Vrijedi
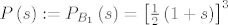 , ,
također je 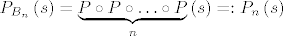 . U ovom se trenutku prisjetimo da je . U ovom se trenutku prisjetimo da je 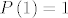 , što nam induktivno povlači da je , što nam induktivno povlači da je 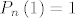 , za svaki , za svaki  . .
Konačno je 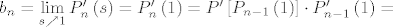
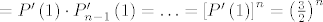 . Druga jednakost vrijedi jer je prva derivacija dobro definirana u točki . Druga jednakost vrijedi jer je prva derivacija dobro definirana u točki 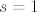 . .
Dakle, trebamo rješiti rekurziju
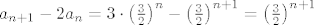 . .
Rješenje pripadajuće homogene jednadžbe 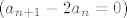 je očito je očito 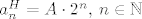 , za neku konstantu , za neku konstantu 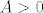 . Iz oblika na desnoj strani rekurzije znamo da je partikularno rješenje oblika . Iz oblika na desnoj strani rekurzije znamo da je partikularno rješenje oblika 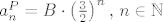 , za neku konstantu , za neku konstantu 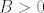 . .
Dakle, rješenje ima oblik 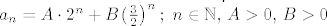 . .
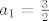 i i 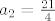 računamo na prste te nalazimo da je računamo na prste te nalazimo da je 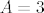 i i 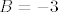 . .
Konačno je
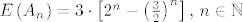 . .
|









