| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mayam
Forumaš(ica)

Pridružen/a: 20. 10. 2010. (18:31:42)
Postovi: (C)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 14:25 pon, 27. 12. 2010 Naslov: Postano: 14:25 pon, 27. 12. 2010 Naslov: |
    |
|
|
Ne moraš odmah svesti na gornjetrokutastu matricu. Zapravo, mala je vjerojatnost da će ti to uspjeti. :) Najčešće ćeš doći do nečeg tipa [latex](\lambda - 3) x = 0[/latex], pa ćeš trebati razlagati na slučajeve. Primijeti da ne smiješ množiti neku jednadžbu s nečim što ovisi o parametru, jer bi moglo ispasti da, za neke vrijednosti parametra, množiš nulom. Množiti jednadžbu nečime i dodavanje u drugu jednadžbu je legalno, jer nije problem ako dodaš nulu.
Toplo ti preporučam da odgađaš množenje nepoznanicama. Npr. čini se najbolje na početku poništavati treći stupac prvim retkom (govorim kao da si već zapisala sustav u matricu).
Ne moraš odmah svesti na gornjetrokutastu matricu. Zapravo, mala je vjerojatnost da će ti to uspjeti.  Najčešće ćeš doći do nečeg tipa Najčešće ćeš doći do nečeg tipa 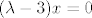 , pa ćeš trebati razlagati na slučajeve. Primijeti da ne smiješ množiti neku jednadžbu s nečim što ovisi o parametru, jer bi moglo ispasti da, za neke vrijednosti parametra, množiš nulom. Množiti jednadžbu nečime i dodavanje u drugu jednadžbu je legalno, jer nije problem ako dodaš nulu. , pa ćeš trebati razlagati na slučajeve. Primijeti da ne smiješ množiti neku jednadžbu s nečim što ovisi o parametru, jer bi moglo ispasti da, za neke vrijednosti parametra, množiš nulom. Množiti jednadžbu nečime i dodavanje u drugu jednadžbu je legalno, jer nije problem ako dodaš nulu.
Toplo ti preporučam da odgađaš množenje nepoznanicama. Npr. čini se najbolje na početku poništavati treći stupac prvim retkom (govorim kao da si već zapisala sustav u matricu).
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:58 pon, 27. 12. 2010 Naslov: Postano: 18:58 pon, 27. 12. 2010 Naslov: |
    |
|
|
[latex]\left[\begin{array}{ccc|c}
1 & \lambda & 1 & -2 \\
-\lambda & -4 & 2 & \mu \\
2 & 3 & 3 & 0
\end{array}\right] & \sim
\left[\begin{array}{ccc|c}
1 & \lambda & 1 & -2 \\
-\lambda - 2 & -4 - 2 \lambda & 0 & \mu + 4 \\
-1 & 3 - 3 \lambda & 0 & 6
\end{array}\right] \sim
\left[\begin{array}{ccc|c}
0 & 3 - 2 \lambda & 1 & 4 \\
0 & (\lambda + 2)(3 \lambda - 5) & 0 & \mu - 6 \lambda - 2 \\
-1 & 3 - 3 \lambda & 0 & 6
\end{array}\right][/latex]
Sad kreće razlaganje na slučajeve:
1° [latex]\lambda = -2[/latex]
[latex]\left[\begin{array}{ccc|c}
0 & 7 & 1 & 4 \\
0 & 0 & 0 & \mu + 4 \\
-1 & 9 & 0 & 6
\end{array}\right][/latex]
1°1° [latex]\mu \neq -4[/latex] Nema rješenja.
1°2° [latex]\mu = -4[/latex]
[latex]\left[\begin{array}{ccc|c}
0 & 7 & 1 & 4 \\
-1 & 9 & 0 & 6
\end{array}\right][/latex] Rješenje je 1-parametarsko: [latex]\left[\begin{array}{c}
x \\ y \\ z
\end{array}\right] = \left[\begin{array}{c}
4 \\ 0 \\ -6
\end{array}\right] + t \left[\begin{array}{c}
-7 \\ 1 \\ 9
\end{array}\right][/latex], [latex]t \in \mathbb{R}[/latex]
2° [latex]\lambda = \frac{5}{3}[/latex]
[latex]\left[\begin{array}{ccc|c}
0 & -\frac{1}{3} & 1 & 4 \\
0 & 0 & 0 & \mu - 12 \\
-1 & -2 & 0 & 6
\end{array}\right][/latex]
2°1° [latex]\mu \neq 12[/latex] Nema rješenja.
2°2° [latex]\mu = 12[/latex]
[latex]\left[\begin{array}{ccc|c}
0 & -\frac{1}{3} & 1 & 4 \\
-1 & -2 & 0 & 6
\end{array}\right][/latex] Rješenje je opet 1-parametarsko.
3° [latex]\lambda \notin \left\{ -2, \frac{5}{3} \right\}[/latex] Rješenje je jedinstveno: [latex]\displaystyle x = -\frac{3 (-12 - \mu + \lambda \mu)}{3 \lambda^2 + \lambda - 10}[/latex], [latex]\displaystyle y = -\frac{8 + 6 \lambda - \mu}{3 \lambda^2 + \lambda - 10}[/latex], [latex]\displaystyle z = -\frac{16 - 6 \lambda + 3 \mu - 2 \lambda \mu}{3 \lambda^2 + \lambda - 10}[/latex].
Možda sam fulao u računanju (dapače, velike su šanse da jesam :)), ali bitna je ideja. :D [size=5]Nadajte se da će i asistenti biti tako raspoloženi.[/size]
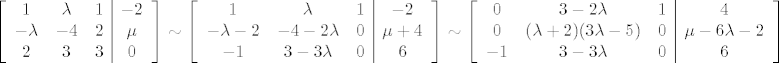
Sad kreće razlaganje na slučajeve:
1° 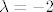

1°1° 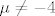 Nema rješenja. Nema rješenja.
1°2° 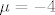
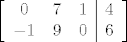 Rješenje je 1-parametarsko: Rješenje je 1-parametarsko: 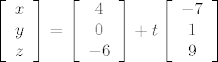 , , 
2° 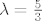
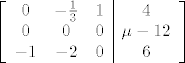
2°1° 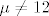 Nema rješenja. Nema rješenja.
2°2° 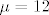
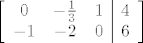 Rješenje je opet 1-parametarsko. Rješenje je opet 1-parametarsko.
3° 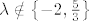 Rješenje je jedinstveno: Rješenje je jedinstveno: 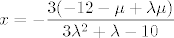 , , 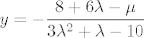 , , 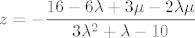 . .
Možda sam fulao u računanju (dapače, velike su šanse da jesam  ), ali bitna je ideja. ), ali bitna je ideja.  Nadajte se da će i asistenti biti tako raspoloženi. Nadajte se da će i asistenti biti tako raspoloženi.
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
|










