|
[quote="123456"]Može pomoć oko ova 2 zadatka. opce nemam ideje...
Je li skup A = {(x1; x2; x3) ∈ C3 : Re x1= Im x2 = −Re x3; Im x1 = −Re x2 = −Im x3}
potprostor kompleksnog vektorskog prostora C3? Ako jest, odredite mu dimenziju i neku
bazu.
[/quote]
[latex]A = \{ (x_1, x_2, x_3) \in \mathbb{C}^3 : Re(x_1)=Im(x_2)=-Re(x_3), Im(x_1)=-Re(x_2)=-Im(x_3) \}[/latex]
s obzirom da je [latex](x_1, x_2, x_3) \in \mathbb{C}^3[/latex] onda su [latex]x_1,x_2,x_3 \in \mathbb{C}[/latex] pa onda ih mogu napisati ovako:
[latex]x_1 = a_1 + a_2\cdot i[/latex]
[latex]x_2 = b_1 + b_2\cdot i[/latex]
[latex]x_3 = c_1 + c_2\cdot i[/latex]
gdje su [latex]a_1,a_2,b_1,b_2,c_1,c_2 \in \mathbb{R}[/latex]
gore iz uvjeta imamo:
[latex]a_1 = b_2 = - c_1[/latex]
[latex]a_2 = - b_1 = - c_2[/latex]
tj.
[latex]x_1 = a_1 + a_2\cdot i[/latex]
[latex]x_2 = - a_2 + a_1\cdot i[/latex]
[latex]x_3 = - a_1 - a_2\cdot i[/latex]
tj.
[latex]A = \{\hspace{2mm} (a_1 + a_2\cdot i, - a_2 + a_1\cdot i, - a_1 - a_2\cdot i ) \in \mathbb{C}^3 \hspace{3mm} |\hspace{3mm} a_1,a_2 \in \mathbb{R} \}[/latex]
sad uzmi dva različita elementa iz A pogledaj dal njihova lin. komb. ostaje u A
| 123456 (napisa): | Može pomoć oko ova 2 zadatka. opce nemam ideje...
Je li skup A = {(x1; x2; x3) ∈ C3 : Re x1= Im x2 = −Re x3; Im x1 = −Re x2 = −Im x3}
potprostor kompleksnog vektorskog prostora C3? Ako jest, odredite mu dimenziju i neku
bazu.
|
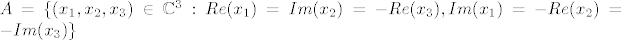
s obzirom da je 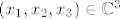 onda su onda su 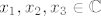 pa onda ih mogu napisati ovako: pa onda ih mogu napisati ovako:
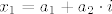
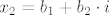
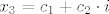
gdje su 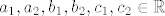
gore iz uvjeta imamo:
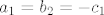
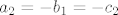
tj.
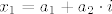
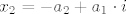
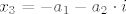
tj.
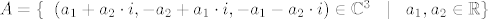
sad uzmi dva različita elementa iz A pogledaj dal njihova lin. komb. ostaje u A
|





