|
Treba samo provjeriti aksiome polja, a lako se vidi da ih dane operacije zadovoljavaju (samo treba koristiti da je [latex]P[/latex] polje sa standardnim operacijama [latex]+, \cdot [/latex] ).
Takodjer iz definicije novih operacija vidi se da ce vrijediti zatvorenost... naime [latex]x, y[/latex] i [latex]a[/latex] su iz [latex]P[/latex] pa ce biti i [latex]x+y-a[/latex] jer je [latex](P,+,\cdot)[/latex] polje. Analogno zakljucujemo za drugu, multiplikativnu operaciju.
Da, na skupu [latex]\mathbb{N}[/latex] ne bi vrijedila zatvorenost, ali [latex](\mathbb{N},+,\cdot)[/latex] nije polje.
Za one koji ne znaju cirilicu, zadatak glasi:
Neka je [latex](P,+,\cdot)[/latex] polje i [latex]a, b[/latex] dva razlicita elementa iz [latex]P[/latex]. Definiramo [latex]*[/latex] i [latex]\circ[/latex] na slijedeci nacin: [latex] x*y = x+y-a,\quad x\circ y = a + \frac{(x-a)(y-a)}{b-a}[/latex]. Dokazi da je [latex](P,*,\circ)[/latex] polje.
Treba samo provjeriti aksiome polja, a lako se vidi da ih dane operacije zadovoljavaju (samo treba koristiti da je  polje sa standardnim operacijama polje sa standardnim operacijama 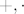 ). ).
Takodjer iz definicije novih operacija vidi se da ce vrijediti zatvorenost... naime 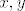 i i  su iz su iz  pa ce biti i pa ce biti i 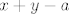 jer je jer je 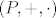 polje. Analogno zakljucujemo za drugu, multiplikativnu operaciju. polje. Analogno zakljucujemo za drugu, multiplikativnu operaciju.
Da, na skupu 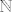 ne bi vrijedila zatvorenost, ali ne bi vrijedila zatvorenost, ali 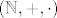 nije polje. nije polje.
Za one koji ne znaju cirilicu, zadatak glasi:
Neka je 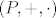 polje i polje i 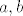 dva razlicita elementa iz dva razlicita elementa iz  . Definiramo . Definiramo  i i  na slijedeci nacin: na slijedeci nacin: 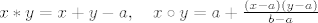 . Dokazi da je . Dokazi da je 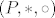 polje. polje.
|





