| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
Alisa
Forumaš(ica)
Pridružen/a: 16. 02. 2008. (15:34:59)
Postovi: (4E)16
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 22:32 sub, 23. 10. 2010 Naslov: Postano: 22:32 sub, 23. 10. 2010 Naslov: |
    |
|
|
[quote="nike"]Može li netko pojasnit rješavanje zadnjeg zadatka u prošlogodišnjem kolokviju (pod b. i c.)
http://web.math.hr/nastava/stat/files/stat-0910-kol1.pdf[/quote]
pod c sam trebaš uvrstiti u onu formulu za umnožak. jer su ti varijable nezavisne, onda je formula za umnožak(propozicija 3.6) integral od minus do plus beskonačno f_X(x)*f_Y(z/x)*1/|x|dx
ovaj pod b mislim da treba računati vjerojatnost da je X-Y<0, a i za to ima formula, propozicija 3.5
pod c sam trebaš uvrstiti u onu formulu za umnožak. jer su ti varijable nezavisne, onda je formula za umnožak(propozicija 3.6) integral od minus do plus beskonačno f_X(x)*f_Y(z/x)*1/|x|dx
ovaj pod b mislim da treba računati vjerojatnost da je X-Y<0, a i za to ima formula, propozicija 3.5
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 3:47 ned, 24. 10. 2010 Naslov: Postano: 3:47 ned, 24. 10. 2010 Naslov: |
    |
|
|
e je, da. ondab ovu funkciju trebalo malo i integrirat. ima i tog na predavanjima, tam ispod propozicija o sumi/produktu
e je, da. ondab ovu funkciju trebalo malo i integrirat. ima i tog na predavanjima, tam ispod propozicija o sumi/produktu
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
 Postano: 18:07 uto, 26. 10. 2010 Naslov: Postano: 18:07 uto, 26. 10. 2010 Naslov: |
    |
|
|
Evo bas gledam 6 zadatak iz proslogodisnjeg kolokvija (pod b).
Pokusavao sam ga rijesiti pomocu onih propozicija sa predavanja ali nije islo, pa sam rijesio na svoj nacin.
Rjesenje je jedako i za (a) i (b) grupu.
Znamo
[latex]
f_{X,Y}(x, y) = f_X(x)f_Y(y)
[/latex]
Obije funkcije su simetrične oko nule pa imamo da je
[latex]f_{X,Y}(x, y) = f_{X,Y}(-x, -y)[/latex]
Zanima nas
[latex]
\mathbb{P}(X>Y) = \int_{X>Y}{f_{X,Y}(x, y)dxdy}
[/latex]
što je
[latex]
\int_{- \infty}^{+ \infty}{\int_{-\infty}^x{f_{X,Y}(x, y)dxdy}}
[/latex]
Zamjenom varijabli [latex](u, v) = (-x, -y)[/latex] dobijemo
[latex]
\int_{-\infty}^{+\infty}{\int_u^{+\infty}{f_{X,Y}(-u, -v)dudv}} =
\int_{-\infty}^{+\infty}{\int_u^{+\infty}{f_{X,Y}(u, v)dudv}} = \mathbb{P}(X<Y)
[/latex]
Dakle, [latex]\mathbb{P}(X>Y) = \mathbb{P}(X<Y) = \frac{1}{2}[/latex]
Mislim da bi to trebalo biti to.
Pozdrav
Evo bas gledam 6 zadatak iz proslogodisnjeg kolokvija (pod b).
Pokusavao sam ga rijesiti pomocu onih propozicija sa predavanja ali nije islo, pa sam rijesio na svoj nacin.
Rjesenje je jedako i za (a) i (b) grupu.
Znamo
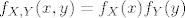
Obije funkcije su simetrične oko nule pa imamo da je

Zanima nas

što je
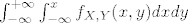
Zamjenom varijabli 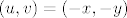 dobijemo dobijemo

Dakle, 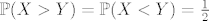
Mislim da bi to trebalo biti to.
Pozdrav
_________________
reductio ad absurdum
|
|
| [Vrh] |
|
malena
Forumaš(ica)

Pridružen/a: 27. 03. 2009. (16:43:42)
Postovi: (62)16
Spol: 
Lokacija: ...
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 0:33 sri, 27. 10. 2010 Naslov: Postano: 0:33 sri, 27. 10. 2010 Naslov: |
    |
|
|
[quote="Anonymous"]Ako ste jos tu, metoda najmanjih kvadrata, ako dobijemo da aproksimiramo funkcijom koja nije pravac sto radimo? Radimo supstituciju da ju svedemo na pravac pa modificiramo podatke ili...???[/quote]
pa koju god funkciju stavi za aproksimaciju uvijek je isto... ( mislim da smo radili sam jednu metodu najmanjih kvadrata, mislim da se ta zove dikretna, jel? )
znači ak treba aproksimirat pravcem pretpostavljam da znaš rješit, pa ću uzet onaj drugi primjer iz nekog odd kolokvija. U zadatku dobijemo neki skup tocaka i trebamo ga aproksimirati funkcijom: [latex]ax^2+b[/latex]
znači uzmemo funkciju:
[latex]\displaystyle{F(a,b) = \sum_{i=1}^{n}( f( x_i ) - ax_{i}^2 - b )^2}[/latex]
( f nam je ona zadana funkcija i imamo njene točke )
i izderiviramo je po a i b i gledamo stacionarne točke ( nultočke tih derivacija ) i dobijemo:
derivacija po a:
[latex]\displaystyle{\sum_{i=1}^{n}x_{i}^2\cdot ( f( x_i ) - ax_{i}^2 - b ) = 0}[/latex]
derivacija po b:
[latex]\displaystyle{\sum_{i=1}^{n}( f( x_i ) - ax_{i}^2 - b ) = 0}[/latex]
i to je to.
| Anonymous (napisa): | | Ako ste jos tu, metoda najmanjih kvadrata, ako dobijemo da aproksimiramo funkcijom koja nije pravac sto radimo? Radimo supstituciju da ju svedemo na pravac pa modificiramo podatke ili...??? |
pa koju god funkciju stavi za aproksimaciju uvijek je isto... ( mislim da smo radili sam jednu metodu najmanjih kvadrata, mislim da se ta zove dikretna, jel? )
znači ak treba aproksimirat pravcem pretpostavljam da znaš rješit, pa ću uzet onaj drugi primjer iz nekog odd kolokvija. U zadatku dobijemo neki skup tocaka i trebamo ga aproksimirati funkcijom: 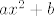
znači uzmemo funkciju:
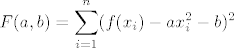
( f nam je ona zadana funkcija i imamo njene točke )
i izderiviramo je po a i b i gledamo stacionarne točke ( nultočke tih derivacija ) i dobijemo:
derivacija po a:
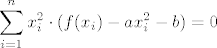
derivacija po b:
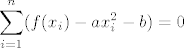
i to je to.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
|















