| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
forumasica13
Forumaš(ica)

Pridružen/a: 17. 11. 2010. (19:14:30)
Postovi: (3)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:48 ned, 5. 12. 2010 Naslov: Postano: 18:48 ned, 5. 12. 2010 Naslov: |
    |
|
|
Ne. Mislim, dobro, da ne ulazimo sad u detalje (generalno, "proizvoljno" razdvajanje na limese baš i ne ide, kao što se možda najbolje vidi iz primjera broja [latex]e[/latex] i njegove definicije), čisto bih htio primijetiti da vrijedi [latex]\displaystyle\lim_{n}\frac{1}{n}=0[/latex], a [latex]\displaystyle\lim_{n}2^n+3^n+4^n=+\infty[/latex]. Stoga ne znam baš koliko bi iznosilo [latex](+\infty)^0[/latex]... :? (A pogotovo zašto bi iznosilo baš [latex]4[/latex]... :D)
U b) dijelu, kao niz [latex](a_n)_n[/latex] uzeli smo konstantan niz jedinica, kao [latex](b_n)_n[/latex] uzeli smo, naravno, niz čiji limes tražimo, a kao [latex](c_n)_n[/latex] niz definiran s [latex]c_n=1+\displaystyle\frac{6^n}{7^n}[/latex]. Kako smo pokazali (uz pomoć ovog međurezultata "desno" od [latex](b_n)_n[/latex], koji lako dokažemo) da vrijedi [latex]a_n\leq b_n\leq c_n[/latex] za sve [latex]n\in\mathbb{N}[/latex], a (očito) [latex]a_n\rightarrow 1[/latex] i [latex]c_n\rightarrow 1[/latex], po Teoremu o sendviču tvrdnja vrijedi.
Ne. Mislim, dobro, da ne ulazimo sad u detalje (generalno, "proizvoljno" razdvajanje na limese baš i ne ide, kao što se možda najbolje vidi iz primjera broja  i njegove definicije), čisto bih htio primijetiti da vrijedi i njegove definicije), čisto bih htio primijetiti da vrijedi 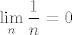 , a , a 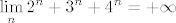 . Stoga ne znam baš koliko bi iznosilo . Stoga ne znam baš koliko bi iznosilo 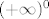 ... ...  (A pogotovo zašto bi iznosilo baš (A pogotovo zašto bi iznosilo baš 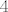 ... ...  ) )
U b) dijelu, kao niz 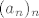 uzeli smo konstantan niz jedinica, kao uzeli smo konstantan niz jedinica, kao 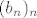 uzeli smo, naravno, niz čiji limes tražimo, a kao uzeli smo, naravno, niz čiji limes tražimo, a kao 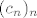 niz definiran s niz definiran s 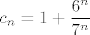 . Kako smo pokazali (uz pomoć ovog međurezultata "desno" od . Kako smo pokazali (uz pomoć ovog međurezultata "desno" od 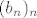 , koji lako dokažemo) da vrijedi , koji lako dokažemo) da vrijedi 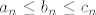 za sve za sve 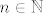 , a (očito) , a (očito)  i i  , po Teoremu o sendviču tvrdnja vrijedi. , po Teoremu o sendviču tvrdnja vrijedi.
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:57 ned, 5. 12. 2010 Naslov: Postano: 23:57 ned, 5. 12. 2010 Naslov: |
    |
|
|
[quote="A-tom"]Zasto smo uzeli bas 1 i 1 + (6/7)^n?[/quote]
Često, kod limesa niza koji liči na razlomak, prvo tražimo što najbrže raste u brojniku, odnosno nazivniku (da znamo čime podijeliti). Konkretno, to je [latex](10 + 3 \cos n)^n[/latex], jer je [latex]7 \leq 10 + 3 \cos n[/latex], pa
[latex](10 + 3 \cos n)^n[/latex] raste barem kao [latex]7^n[/latex]. Kad time podijelimo brojnik i nazivnik, dobivamo [latex]\displaystyle \frac{1 + \frac{6^n}{(10 + 3 \cos n)^n}}{1 + \frac{3^n}{(10 + 3 \cos n)^n}}[/latex]. Sad je jasno [latex]\displaystyle 1 \leq \frac{1 + \frac{6^n}{(10 + 3 \cos n)^n}}{1 + \frac{3^n}{(10 + 3 \cos n)^n}} \leq 1 + \frac{6^n}{(10 + 3 \cos n)^n} \leq 1 + \frac{6^n}{7^n}[/latex].
Naravno, to nisu jedine "dozvoljene" ograde. Možemo uzeti i [latex]\displaystyle \frac{1 + \frac{6^n}{13^n}}{1 + \frac{3^n}{7^n}} \leq \frac{1 + \frac{6^n}{(10 + 3 \cos n)^n}}{1 + \frac{3^n}{(10 + 3 \cos n)^n}} \leq \frac{1 + \frac{6^n}{7^n}}{1 + \frac{3^n}{13^n}}[/latex].
[quote="A-tom"]a) podzatak razumijem gdje sam pogrjesila no mozes li mi objasniti na koji su nacin oni to rjesili? opet pomocu teorema o sendvicu, no kako su dosli do lijeve i desne stane nejednakosti?[/quote]
Možda će ovako biti jasnije: [latex]\displaystyle 4 = \sqrt[n]{0 + 0 + 4^n} \leq \sqrt[n]{2^n + 3^n + 4^n} \leq \sqrt[n]{4^n + 4^n + 4^n} = \sqrt[n]{3 \cdot 4^n} = 4 \sqrt[n]{3}[/latex].
| A-tom (napisa): | | Zasto smo uzeli bas 1 i 1 + (6/7)^n? |
Često, kod limesa niza koji liči na razlomak, prvo tražimo što najbrže raste u brojniku, odnosno nazivniku (da znamo čime podijeliti). Konkretno, to je 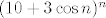 , jer je , jer je 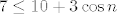 , pa , pa
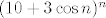 raste barem kao raste barem kao 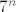 . Kad time podijelimo brojnik i nazivnik, dobivamo . Kad time podijelimo brojnik i nazivnik, dobivamo 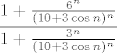 . Sad je jasno . Sad je jasno 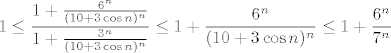 . .
Naravno, to nisu jedine "dozvoljene" ograde. Možemo uzeti i  . .
| A-tom (napisa): | | a) podzatak razumijem gdje sam pogrjesila no mozes li mi objasniti na koji su nacin oni to rjesili? opet pomocu teorema o sendvicu, no kako su dosli do lijeve i desne stane nejednakosti? |
Možda će ovako biti jasnije: 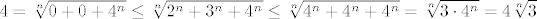 . .
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
|











