| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 0:09 ned, 19. 12. 2010 Naslov: Postano: 0:09 ned, 19. 12. 2010 Naslov: |
    |
|
|
1. Rješava se na istu foru kao i ostali tog tipa. Samo treba pripaziti kod dokaza ograničenosti i monotonosti indukcijom koje rastuće funkcije se koriste. One su [latex]x \mapsto x^2 + c[/latex] i [latex]x \mapsto \frac{1}{6} x + c[/latex]. Prva je rastuća samo za [latex]x \geq 0[/latex], ali vidimo iz početnih članova niza i rekurzije da je [latex]a_n \geq 0[/latex], za sve [latex]n[/latex], pa je sve OK.
3. Treba iskoristiti da je sh strogo rastuća funkcija i zatim podijeliti na uniju, ovisno parnosti od [latex]n[/latex].
Evo, vjerojatno nisam sve jasno i precizno objasnio, pa slobodno reci ako treba nešto razjasniti. :D
1. Rješava se na istu foru kao i ostali tog tipa. Samo treba pripaziti kod dokaza ograničenosti i monotonosti indukcijom koje rastuće funkcije se koriste. One su 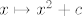 i i 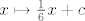 . Prva je rastuća samo za . Prva je rastuća samo za 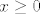 , ali vidimo iz početnih članova niza i rekurzije da je , ali vidimo iz početnih članova niza i rekurzije da je 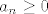 , za sve , za sve  , pa je sve OK. , pa je sve OK.
3. Treba iskoristiti da je sh strogo rastuća funkcija i zatim podijeliti na uniju, ovisno parnosti od  . .
Evo, vjerojatno nisam sve jasno i precizno objasnio, pa slobodno reci ako treba nešto razjasniti. 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:44 ned, 19. 12. 2010 Naslov: Postano: 12:44 ned, 19. 12. 2010 Naslov: |
    |
|
|
Ako te samo taj sh muči, nemaš problema :), jer ako označimo [latex]\displaystyle T = \left\{ \frac{(-1)^n + 2 n}{n \sin \left( \frac{(-1)^{n - 1} \pi}{2} \right)} : n \in \mathbb{N} \right\}[/latex], onda je [latex]S = \sinh T[/latex]. Kako je sh strogo rastuća, vrijedi [latex]\inf S = \sinh \inf T[/latex] i [latex]\sup S = \sinh \sup T[/latex]. Dakle, samo treba odrediti infimum i supremum od [latex]T[/latex].
U prvom treba pokazati da je [latex]a_n \leq a_{n + 1}[/latex], za svaki [latex]n \in \mathbb{N}[/latex].
Baza: Provjerimo za [latex]n = 1[/latex] i [latex]n = 2[/latex].
Korak: Pretpostavimo da za neki [latex]n \in \mathbb{N}[/latex] vrijedi [latex]a_n \leq a_{n + 1}[/latex] i [latex]a_{n + 1} \leq a_{n + 2}[/latex]. Slijedi da je [latex]\displaystyle a_{n + 3} = a_{n + 2}^2 + \frac{1}{6} a_{n + 1} + \frac{1}{9} \geq a_{n + 1}^2 + \frac{1}{6} a_{n + 1} + \frac{1}{9} \geq a_{n + 1}^2 + \frac{1}{6} a_n + \frac{1}{9} = a_{n + 2}[/latex]. Koristio sam ono što sam napomenuo gore o rastućim funkcijama.
Ako te samo taj sh muči, nemaš problema  , jer ako označimo , jer ako označimo 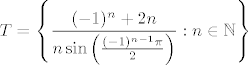 , onda je , onda je 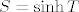 . Kako je sh strogo rastuća, vrijedi . Kako je sh strogo rastuća, vrijedi 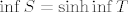 i i 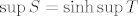 . Dakle, samo treba odrediti infimum i supremum od . Dakle, samo treba odrediti infimum i supremum od  . .
U prvom treba pokazati da je 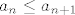 , za svaki , za svaki  . .
Baza: Provjerimo za 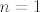 i i  . .
Korak: Pretpostavimo da za neki  vrijedi vrijedi 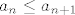 i i 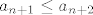 . Slijedi da je . Slijedi da je 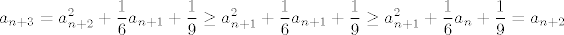 . Koristio sam ono što sam napomenuo gore o rastućim funkcijama. . Koristio sam ono što sam napomenuo gore o rastućim funkcijama.
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:02 sri, 5. 1. 2011 Naslov: Postano: 13:02 sri, 5. 1. 2011 Naslov: |
    |
|
|
Ma da, u svima je ista fora, riješio sam negdje ovaj iz druge grupe tu na forumu, idem vidjeti...
Aha, evo: i prva grupa (pbakic) i druga grupa (ja) su [url=http://degiorgi.math.hr/forum/viewtopic.php?t=15982]tu[/url]. Poanta je samo da shvatiš da ovo unutar korijena "izgleda kao" [latex]e^n[/latex] (dobro, zapravo [latex]\displaystyle\frac{e^n}{2}[/latex], ali to nam je nebitno jer korijen ubije dvojku). Naime i sinus hiperbolni i kosinus hiperbolni tako izgledaju za velike [latex]n[/latex] (jer je tada [latex]e^{-n}[/latex] zanemarivo prema [latex]e^n[/latex]), a i tangens hiperbolni i arkus tangens su ograničeni, pa su i oni zanemarivi prema [latex]e^n[/latex].
Ma da, u svima je ista fora, riješio sam negdje ovaj iz druge grupe tu na forumu, idem vidjeti...
Aha, evo: i prva grupa (pbakic) i druga grupa (ja) su tu. Poanta je samo da shvatiš da ovo unutar korijena "izgleda kao" 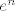 (dobro, zapravo (dobro, zapravo 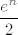 , ali to nam je nebitno jer korijen ubije dvojku). Naime i sinus hiperbolni i kosinus hiperbolni tako izgledaju za velike , ali to nam je nebitno jer korijen ubije dvojku). Naime i sinus hiperbolni i kosinus hiperbolni tako izgledaju za velike  (jer je tada (jer je tada 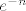 zanemarivo prema zanemarivo prema 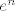 ), a i tangens hiperbolni i arkus tangens su ograničeni, pa su i oni zanemarivi prema ), a i tangens hiperbolni i arkus tangens su ograničeni, pa su i oni zanemarivi prema 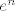 . .
|
|
| [Vrh] |
|
|








