| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:44 sri, 5. 1. 2011 Naslov: Postano: 12:44 sri, 5. 1. 2011 Naslov: |
    |
|
|
Ti, naravno, shvaćaš da tu ima dvije grupe, a u svakoj ima 2 podzadatka? :D Pretpostavljam da tražiš samo rješenje, a ne i nekakav postupak, pa ću ja napisati za sve grupe, a onda reci ako trebaju neki detaljniji hintovi negdje (a onda bi bilo vjerojatno smisleno i da kažeš dokle si došao :)).
Dakle, rješenja su (bar mislim) redom: [latex]2[/latex], [latex]-0.5[/latex], [latex]3[/latex] i [latex]-2[/latex].
Ti, naravno, shvaćaš da tu ima dvije grupe, a u svakoj ima 2 podzadatka?  Pretpostavljam da tražiš samo rješenje, a ne i nekakav postupak, pa ću ja napisati za sve grupe, a onda reci ako trebaju neki detaljniji hintovi negdje (a onda bi bilo vjerojatno smisleno i da kažeš dokle si došao Pretpostavljam da tražiš samo rješenje, a ne i nekakav postupak, pa ću ja napisati za sve grupe, a onda reci ako trebaju neki detaljniji hintovi negdje (a onda bi bilo vjerojatno smisleno i da kažeš dokle si došao  ). ).
Dakle, rješenja su (bar mislim) redom:  , , 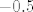 , , 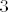 i i 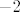 . .
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:54 čet, 6. 1. 2011 Naslov: Postano: 18:54 čet, 6. 1. 2011 Naslov: |
    |
|
|
Hm, da, netipičan malo zadatak. U svakom slučaju, ideja je zamijeniti kosinus unutra sa sinusom, pa da nam se arkus sinusa i sinus "pokrate".
Dakle, iskoristit ćemo da je [latex]\displaystyle\cos(x)=\sin(x-\frac{3\pi}{2})[/latex]. Ovaj [latex]3\pi/2[/latex] možda nije bio najintuitivniji za izabrati na prvi pogled, ali to smo napravili jer nam je onda [latex]\displaystyle x-\frac{3\pi}{2}\in[-\frac{\pi}{2},\frac{\pi}{2}][/latex], a to je kodomena arkus sinusa.
Sad, dakle, imamo [latex]\displaystyle\mathrm{arcsin }(\sin(x-\frac{3\pi}{2}))[/latex]. Kako znamo da je arkus sinusa baš na gornjem intervalu inverzna funkcija sinusu, sad znamo da to iznosi upravo [latex]\displaystyle x-\frac{3\pi}{2}[/latex]. Dakle, [latex]a=1[/latex], [latex]b=-3\pi/2[/latex].
Evo, a drugi probaj ti sam, da ne uništavam zabavu. :) Princip je potpuno isti, samo što se radi o tangensu i kotangensu. Reci ako bude trebalo kakvih hintova. :)
Hm, da, netipičan malo zadatak. U svakom slučaju, ideja je zamijeniti kosinus unutra sa sinusom, pa da nam se arkus sinusa i sinus "pokrate".
Dakle, iskoristit ćemo da je 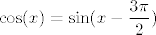 . Ovaj . Ovaj 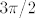 možda nije bio najintuitivniji za izabrati na prvi pogled, ali to smo napravili jer nam je onda možda nije bio najintuitivniji za izabrati na prvi pogled, ali to smo napravili jer nam je onda 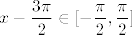 , a to je kodomena arkus sinusa. , a to je kodomena arkus sinusa.
Sad, dakle, imamo 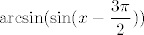 . Kako znamo da je arkus sinusa baš na gornjem intervalu inverzna funkcija sinusu, sad znamo da to iznosi upravo . Kako znamo da je arkus sinusa baš na gornjem intervalu inverzna funkcija sinusu, sad znamo da to iznosi upravo 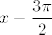 . Dakle, . Dakle, 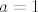 , , 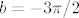 . .
Evo, a drugi probaj ti sam, da ne uništavam zabavu.  Princip je potpuno isti, samo što se radi o tangensu i kotangensu. Reci ako bude trebalo kakvih hintova. Princip je potpuno isti, samo što se radi o tangensu i kotangensu. Reci ako bude trebalo kakvih hintova. 
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
|







