|
[quote="patlidzan"]http://web.math.hr/nastava/uuv/kolokviji/vjer-0809-kol1.pdf
Dali bi netko mogao objasnit kako se rješava 4. zadatak.[/quote]
Brutalnom silom (govorim o b) i c), a) ti je valjda jasan :)). Ako se pravovremeno uoči da traženi skupovi moraju imati nešto u presjeku, onda backtracking-om. :)
[quote="patlidzan"]http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf
i jel bi mogao netko prvi i drugi riješit[/quote]
1.a) [latex]P(A^c \cup B) = 1 - P(A \cap B^c) = 1 - P(A \setminus B)[/latex]
b) [latex]P(A|B) = \frac{P(A \cap B)}{P(B)}[/latex], [latex]P(A \cap B) = P(A) - P(A \setminus B)[/latex]
c) [latex]P(A \cap B) \stackrel{??}{=} P(A) P(B)[/latex]
2.a) Atomi su: [latex][0, 1][/latex], [latex]\langle 1, 2][/latex], [latex]\langle 2, 3][/latex], [latex]\langle 3, 4][/latex], [latex]\langle 4, 5][/latex] i [latex]\langle 5, 10][/latex].
b) [latex]\displaystyle \limsup_{n \to \infty} \left[ \frac{1}{n}, 5 + \frac{1}{n} \right] = \bigcap_{n = 1}^{\infty} \bigcup_{k = n}^{\infty} \left[ \frac{1}{k}, 5 + \frac{1}{k} \right] = \bigcap_{n = 1}^{\infty} \left\langle 0, 5 + \frac{1}{n} \right] = \left\langle 0, 5 \right][/latex]
| patlidzan (napisa): | http://web.math.hr/nastava/uuv/kolokviji/vjer-0809-kol1.pdf
Dali bi netko mogao objasnit kako se rješava 4. zadatak. |
Brutalnom silom (govorim o b) i c), a) ti je valjda jasan  ). Ako se pravovremeno uoči da traženi skupovi moraju imati nešto u presjeku, onda backtracking-om. ). Ako se pravovremeno uoči da traženi skupovi moraju imati nešto u presjeku, onda backtracking-om. 
| patlidzan (napisa): | http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf
i jel bi mogao netko prvi i drugi riješit |
1.a) 
b)  , , 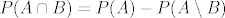
c) 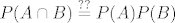
2.a) Atomi su:  , , 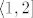 , , 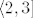 , ,  , , 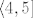 i i 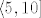 . .
b) 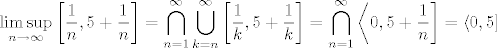
|






