|
Onda je prvi na redu taj s a) i b). :D
Kao što je iskazana želja, preskočiti ću trivijalni smjer! :)
Neka je, dakle
a) [latex]\Phi\left(x,\, x\right)=\mathrm{\bold I},\ \forall x \in I[/latex] i
b) [latex]\left(\frac{\partial}{\partial x}\Phi\left(x,\, y\right)\right)\Phi^{-1}\left(x,\, y\right)=B\left(x\right),\ \forall x,\, y \in I[/latex], gdje je [latex]B \in C\left(I;\, \mathbb{M}_n\left(\mathbb{R}\right)\right)[/latex]. Ovo svojstvo će nam biti korisnije u obliku [latex]\frac{\partial}{\partial x}\Phi\left(x,\, y\right)=B\left(x\right)\Phi\left(x,\, y\right),\ \forall x,\, y \in I[/latex].
Pokazati ćemo da je [latex]\Phi[/latex] evoluciona matrica sustava [latex]\frac{d}{dx}U=B\left(x\right)U\ (*)[/latex].
Neka je [latex]W[/latex] bilo koja fundamentalna matrica sustava [latex](*)[/latex], znamo da takva postoji zbog uvjeta u kojima se nalazimo. Neka je [latex]\widehat{\Phi}\left(x,\, y\right)=W\left(x\right)W^{-1}\left(y\right),\ \forall x,\, y \in I[/latex] evoluciona matrica sustava [latex](*)[/latex]. Sada je dovoljno pokazati da je [latex]\Phi\left(x, y\right)=\widehat{\Phi}\left(x,\, y\right),\ \forall x,\, y \in I[/latex].
Navedimo svojstva matrice [latex]\widehat{\Phi}[/latex] koja ćemo koristiti:
1) [latex]\widehat{\Phi}\left(x,\, x\right)=\mathrm{\bold I},\ \forall x \in I[/latex],
2) [latex]\widehat{\Phi}^{-1}\left(x,\, y\right)=\left(W\left(x\right)W^{-1}\left(y\right)\right)^{-1}=W\left(y\right)W^{-1}\left(x\right)=\widehat{\Phi}\left(y,\, x\right)[/latex].
3) [latex]\frac{\partial}{\partial y}\widehat{\Phi}\left(x,\, y\right)=-\widehat{\Phi}\left(x,\, y\right)B\left(y\right),\ \forall x,\, y \in I[/latex],
Uočimo sada da ukoliko pokažemo da je [latex]\Phi\left(x,\, y\right)=\widehat{\Phi}\left(x,\, y\right)C,\ \forall x,\, y \in I\ (**)[/latex], gdje je [latex]C \in \mathbb{M}_n\left(\mathbb{R}\right)[/latex] konstantna regularna matrica da smo gotovi jer onda iz svojstava a) i 1) slijedi da je [latex]C=\mathtrm{\bold I}[/latex]. Dalje računamo
[latex](**) \Longleftrightarrow \widehat{\Phi}^{-1}\left(x,\, y\right)\Phi\left(x,\, y\right)=C \Longleftrightarrow \widehat{\Phi}\left(y,\, x\right)\Phi\left(x,\, y\right)=C \mid \frac{\partial}{\partial x}[/latex]. Dobivamo da je dovoljno pokazati da je
[latex]\frac{\partial}{\partial x}\widehat{\Phi}\left(y,\, x\right)\Phi\left(x,\, y\right)+\widehat{\Phi}\left(y,\, x\right)\frac{\partial}{\partial x}\Phi\left(x,\, y\right)=0[/latex]. No, posljednje je ekvivalentno s
[latex]-\widehat{\Phi}\left(y,\, x\right)B\left(x\right)\Phi\left(x,\, y\right)+\widehat{\Phi}\left(y,\, x\right)B\left(x\right)\Phi\left(x,\, y\right)=0 \Longleftrightarrow 0=0[/latex].
[latex]Q.E.D.[/latex] :)
Drugi, po meni znatno lakši teoretski zadatak od lani.
[b]1)[/b] Neka je [latex]\Phi[/latex] fundamentalna matrica sustava [latex]\frac{d}{dx}U=-A^{\tau}\left(x\right)U[/latex], odnosno, vrijedi [latex]\frac{d}{dx}\Phi=-A^{\tau}\left(x\right)\Phi\ (*)[/latex]. Moramo pokazati da je
[latex]\Phi^{\tau}\left(x\right)W\left(x\right)=C,\ \forall x \in I[/latex], gdje je [latex]C \in \mathbb{M}_n\left(\mathbb{R}\right)[/latex] konstantna regularna matrica. Napadnemo li to sa [latex]\frac{d}{dx}[/latex] vidimo da je dovoljno pokazati
[latex]\frac{d}{dx}\Phi^{\tau}\left(x\right)W\left(x\right)+\Phi^{\tau}\left(x\right)\frac{d}{dx}W\left(x\right)=0[/latex], sada transponiranjem jednakosti [latex](*)[/latex] i korištenjem onoga što znamo o [latex]W[/latex] dobivamo [latex]0=0[/latex], ovime je prvi smjer gotov.
[b]2)[/b] Neka je [latex]C \in \mathbb{M}_n\left(\mathbb{R}\right)[/latex] konstantna regularna matrica takva da je [latex]\Phi^{\tau}\left(x\right)W\left(x\right)=C,\ \forall x \in I[/latex]. Kako su [latex]W[/latex] i [latex]C[/latex] regularne odmah zaključujemo da je i [latex]\Phi[/latex] regularna.
Vidimo da vrijedi [latex]\Phi=W^{-\tau}C^{\tau}[/latex], odnosno [latex]\frac{d}{dx}\Phi=\frac{d}{dx}W^{-\tau}C^{\tau}[/latex].
Vrijedi [latex]\frac{d}{dx}W^{-1}=-W^{-1}A[/latex], odnosno [latex]\frac{d}{dx}W^{-\tau}=-A^{\tau}W^{-\tau}=-A^{\tau}\Phi C^{-\tau}[/latex]. Ovo zadnje dobijemo iz početnog uvjeta. Konačno smo dobili
[latex]\frac{d}{dx}\Phi\left(x\right)=-A^{\tau}\left(x\right)\Phi\left(x\right),\ \forall x \in I[/latex].
[latex]Q.E.D.[/latex] :)
Onda je prvi na redu taj s a) i b). 
Kao što je iskazana želja, preskočiti ću trivijalni smjer! 
Neka je, dakle
a) 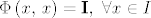 i i
b) 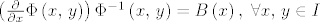 , gdje je , gdje je 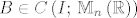 . Ovo svojstvo će nam biti korisnije u obliku . Ovo svojstvo će nam biti korisnije u obliku 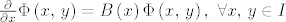 . .
Pokazati ćemo da je 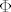 evoluciona matrica sustava evoluciona matrica sustava 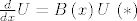 . .
Neka je 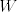 bilo koja fundamentalna matrica sustava bilo koja fundamentalna matrica sustava  , znamo da takva postoji zbog uvjeta u kojima se nalazimo. Neka je , znamo da takva postoji zbog uvjeta u kojima se nalazimo. Neka je 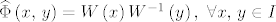 evoluciona matrica sustava evoluciona matrica sustava  . Sada je dovoljno pokazati da je . Sada je dovoljno pokazati da je 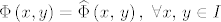 . .
Navedimo svojstva matrice 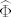 koja ćemo koristiti: koja ćemo koristiti:
1) 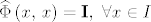 , ,
2) 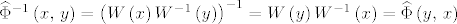 . .
3) 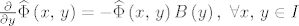 , ,
Uočimo sada da ukoliko pokažemo da je 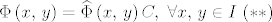 , gdje je , gdje je 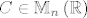 konstantna regularna matrica da smo gotovi jer onda iz svojstava a) i 1) slijedi da je konstantna regularna matrica da smo gotovi jer onda iz svojstava a) i 1) slijedi da je 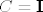 . Dalje računamo . Dalje računamo
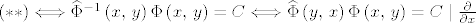 . Dobivamo da je dovoljno pokazati da je . Dobivamo da je dovoljno pokazati da je
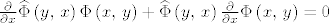 . No, posljednje je ekvivalentno s . No, posljednje je ekvivalentno s
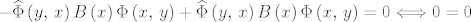 . .
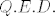 
Drugi, po meni znatno lakši teoretski zadatak od lani.
1) Neka je 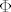 fundamentalna matrica sustava fundamentalna matrica sustava 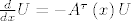 , odnosno, vrijedi , odnosno, vrijedi 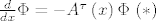 . Moramo pokazati da je . Moramo pokazati da je
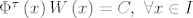 , gdje je , gdje je 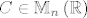 konstantna regularna matrica. Napadnemo li to sa konstantna regularna matrica. Napadnemo li to sa 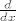 vidimo da je dovoljno pokazati vidimo da je dovoljno pokazati
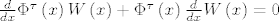 , sada transponiranjem jednakosti , sada transponiranjem jednakosti  i korištenjem onoga što znamo o i korištenjem onoga što znamo o 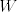 dobivamo dobivamo 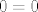 , ovime je prvi smjer gotov. , ovime je prvi smjer gotov.
2) Neka je 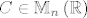 konstantna regularna matrica takva da je konstantna regularna matrica takva da je 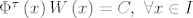 . Kako su . Kako su 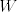 i i  regularne odmah zaključujemo da je i regularne odmah zaključujemo da je i 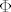 regularna. regularna.
Vidimo da vrijedi 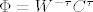 , odnosno , odnosno 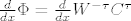 . .
Vrijedi 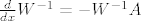 , odnosno , odnosno 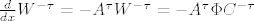 . Ovo zadnje dobijemo iz početnog uvjeta. Konačno smo dobili . Ovo zadnje dobijemo iz početnog uvjeta. Konačno smo dobili
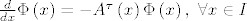 . .
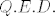 
|






