| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Blondie
Forumaš(ica)


Pridružen/a: 16. 11. 2009. (15:11:18)
Postovi: (47)16
Spol: 
|
 Postano: 20:50 sub, 4. 12. 2010 Naslov: polinom(i) Postano: 20:50 sub, 4. 12. 2010 Naslov: polinom(i) |
    |
|
|
1zad) Za polinom [latex]f(x)=(x^3)-x[/latex] odredi polinom [latex]f(x-1)+f(x)+f(x+1)[/latex].
Rj:
[latex](x^3-x-1)+(x^3-x)+(x^3-x+1)= 3(x^3)-3x[/latex]
2zad)Za polinom [latex]f(x)=2(x^4)-(x^3)[/latex] odredi polinom [latex]f(x+1)-f(x)[/latex].
Rj:
[latex]2((x+1)^4)-((x+1)^3)-(2(x^4)-(x^3))=8x^3+9x^2+5x+1[/latex]
ok, nadam se da nisam fulala koju zagradu/x/+/-...
nego, moje pitanje je, imam iste zadatke zadane, a riješila sam ih na drugačiji način. riješnja su dobra jer sam ih provjerila na kraju knjige :)
kak da znam koji put moram koji način koristiti? :sigh:
1zad) Za polinom 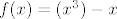 odredi polinom odredi polinom 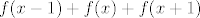 . .
Rj:
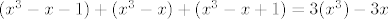
2zad)Za polinom 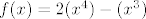 odredi polinom odredi polinom 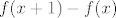 . .
Rj:
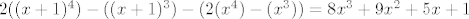
ok, nadam se da nisam fulala koju zagradu/x/+/-...
nego, moje pitanje je, imam iste zadatke zadane, a riješila sam ih na drugačiji način. riješnja su dobra jer sam ih provjerila na kraju knjige 
kak da znam koji put moram koji način koristiti? 
_________________
Dijeliti restoran ili lokal na pušačku i nepušačku sekciju je kao da podijelite bazen na dvije polovice
- u jednoj smijes pišati, u drugoj ne.
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Blondie
Forumaš(ica)


Pridružen/a: 16. 11. 2009. (15:11:18)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Blondie
Forumaš(ica)


Pridružen/a: 16. 11. 2009. (15:11:18)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 1:57 pon, 13. 12. 2010 Naslov: Postano: 1:57 pon, 13. 12. 2010 Naslov: |
    |
|
|
[quote="Blondie"]mislila sam na [latex](1/2)x^2[/latex][/quote]
Ma, naravno, jer je polinom. Ali radije isprobam obje mogucnosti, kad nije jasno koja je.
[quote="Blondie"]idem onda opet sad probat uočit grešku[/quote]
Ne znam kako radis. Ja bih ovako:
1. zakljuciti da je triv. rjesenje nul-polinom (da dalje ne moramo misliti na tu mogucnost),
2. zakljuciti da je stupanj polinoma 2 i zapisati u opcenitoj formi (parametri a, b, c),
3. uvrstiti nesto pametno (npr. nultocku polinoma, za koju ne moramo znati koja je) i eliminirati nesto (npr. parametar c),
4. rijesiti do kraja.
| Blondie (napisa): | mislila sam na 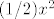 |
Ma, naravno, jer je polinom. Ali radije isprobam obje mogucnosti, kad nije jasno koja je.
| Blondie (napisa): | | idem onda opet sad probat uočit grešku |
Ne znam kako radis. Ja bih ovako:
1. zakljuciti da je triv. rjesenje nul-polinom (da dalje ne moramo misliti na tu mogucnost),
2. zakljuciti da je stupanj polinoma 2 i zapisati u opcenitoj formi (parametri a, b, c),
3. uvrstiti nesto pametno (npr. nultocku polinoma, za koju ne moramo znati koja je) i eliminirati nesto (npr. parametar c),
4. rijesiti do kraja.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:32 ned, 19. 12. 2010 Naslov: polinom(i) Postano: 12:32 ned, 19. 12. 2010 Naslov: polinom(i) |
    |
|
|
Pokušavam riješiti
Odredite sve polinome [latex]f\in\mathbb R[x][/latex] koji zadovoljavaju polinomsku jednadžbu
[latex]x\cdot f(x-1)=(x-3)f(x),\quad \forall x\in\mathbb R[/latex]
Uvrstio sam nulišta,
[latex]x=0\qquad 0=-3\cdot f(0)\implies f(0)=0\implies x\mid f(x)\\x=3\qquad 3\cdot f(2)=0\implies f(2)=0\implies (x-2)\mid f(x)\\x=1\qquad \underbrace{1\cdot f(0)}_{=0}=-2f(1)\implies f(1)=0\implies (x-1)\mid f(x)[/latex]
pa će i njihov produkt [latex]x(x-1)(x-2)\mid f(x)[/latex]
Sada je [latex]f(x)=q(x)\cdot x(x-1)(x-2)[/latex]
Natrag u polaznu jednakost [latex]x\cdot f(x-1)=(x-3)f(x)[/latex] jer se traži funkcijska vrijednost u algebarskom izrazu
[latex]x\cdot q(x-1)\cdot (x-1)(x-2)(x-3)=(x-3)\cdot q(x)\cdot x(x-1)(x-2)[/latex], reduciraju se 4 faktora lijevo i 4 desno, i dobije se
[latex]q(x-1)=q(x) \quad \forall x\ne 0, 1, 2, 3.[/latex]
Posebnao za [latex]x=4, 5, 6, 7, .....[/latex] je: [latex]q(3)=q(4)\\q(4)=q(5)\\q(5)=q(6)\\q(6)=q(7)............[/latex]
I ja sad neznam dalje. Koji potez treba učiniti i [u]zašto [/u]taj potez? Može li netko privući konačnom rješenju [latex]f(x)=c\cdot x(x-1)(x-2), \quad c\in \mathbb R[/latex]
Pokušavam riješiti
Odredite sve polinome 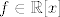 koji zadovoljavaju polinomsku jednadžbu koji zadovoljavaju polinomsku jednadžbu

Uvrstio sam nulišta,
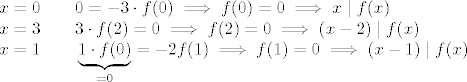
pa će i njihov produkt 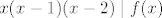
Sada je 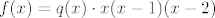
Natrag u polaznu jednakost 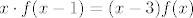 jer se traži funkcijska vrijednost u algebarskom izrazu jer se traži funkcijska vrijednost u algebarskom izrazu
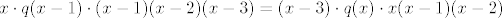 , reduciraju se 4 faktora lijevo i 4 desno, i dobije se , reduciraju se 4 faktora lijevo i 4 desno, i dobije se
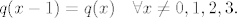
Posebnao za 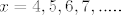 je: je: 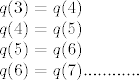
I ja sad neznam dalje. Koji potez treba učiniti i zašto taj potez? Može li netko privući konačnom rješenju 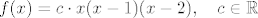
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:08 ned, 19. 12. 2010 Naslov: Postano: 13:08 ned, 19. 12. 2010 Naslov: |
    |
|
|
Da sad ne proucavam sve sto si napisao, fixirajmo neki [latex]x_0 > 3[/latex] (ovo veci od 3 je samo zato da ne moramo mozgati je l' dosadasnje nultocke negdje smetaju, pa da nismo smjeli pokratiti).
Tada je [latex]r(x) := q(x) - q(x_0)[/latex] opet polinom i vrijedi
[latex]r(x_0 + k) = 0[/latex] za sve prirodne [i]k[/i].
To je polinom s beskonacno mnogo nultocaka, dakle nul-polinom, pa je [i]q[/i] konstantni polinom, tj. [latex]q(x) = c[/latex].
Da sad ne proucavam sve sto si napisao, fixirajmo neki  (ovo veci od 3 je samo zato da ne moramo mozgati je l' dosadasnje nultocke negdje smetaju, pa da nismo smjeli pokratiti). (ovo veci od 3 je samo zato da ne moramo mozgati je l' dosadasnje nultocke negdje smetaju, pa da nismo smjeli pokratiti).
Tada je 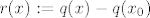 opet polinom i vrijedi opet polinom i vrijedi
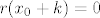 za sve prirodne k. za sve prirodne k.
To je polinom s beskonacno mnogo nultocaka, dakle nul-polinom, pa je q konstantni polinom, tj. 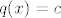 . .
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
BeeBee
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (16:07:39)
Postovi: (79)16
|
 Postano: 13:52 ned, 19. 12. 2010 Naslov: Re: polinom(i) Postano: 13:52 ned, 19. 12. 2010 Naslov: Re: polinom(i) |
    |
|
|
Može li netko privući konačnom rješenju [latex]f(x)=c\cdot x(x-1)(x-2), \quad c\in \mathbb R[/latex][/quote]
Ako uvrstimo nultočke of f (0,3,1) dobijemo: f(0)=0, f(2)=0, f(1)=0. Dalje po Bezotovom teoremu slijedi da t0,t1,t2 dijeli f tj t0*t1*t2 / f
To možemo zapisati u sljedećem obliku: f(x)=x(x-1)(x-2)q(x). Označimo ovu jednadžbu sa *
Ako * uvrstimo u početnu jednadžbu umjesto f(x) dobivamo q(x-1)=q(x) za svaki X iz R\{0,1,2,3}, a to specijalno znači q(4)=q(5)=q(6)=...:= c (konst.)
p(x):=q(x)-c , nultočaka je beskonačno, N\{1,2,3}
Za svaki x iz R je p(x)=0 :
q(x)=p(x)+c=0+c=c za svaki x iz R, dakle f(x)=cx(x-1)(x-2) za neki c iz R
Ako i dalje nije jasno, dođi na demonstrature u srijedu :)
Može li netko privući konačnom rješenju 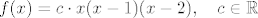 [/quote] [/quote]
Ako uvrstimo nultočke of f (0,3,1) dobijemo: f(0)=0, f(2)=0, f(1)=0. Dalje po Bezotovom teoremu slijedi da t0,t1,t2 dijeli f tj t0*t1*t2 / f
To možemo zapisati u sljedećem obliku: f(x)=x(x-1)(x-2)q(x). Označimo ovu jednadžbu sa *
Ako * uvrstimo u početnu jednadžbu umjesto f(x) dobivamo q(x-1)=q(x) za svaki X iz R\{0,1,2,3}, a to specijalno znači q(4)=q(5)=q(6)=...:= c (konst.)
p(x):=q(x)-c , nultočaka je beskonačno, N\{1,2,3}
Za svaki x iz R je p(x)=0 :
q(x)=p(x)+c=0+c=c za svaki x iz R, dakle f(x)=cx(x-1)(x-2) za neki c iz R
Ako i dalje nije jasno, dođi na demonstrature u srijedu 
|
|
| [Vrh] |
|
Blondie
Forumaš(ica)


Pridružen/a: 16. 11. 2009. (15:11:18)
Postovi: (47)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
BeeBee
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (16:07:39)
Postovi: (79)16
|
|
| [Vrh] |
|
|













