| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:32 pet, 26. 11. 2010 Naslov: Postano: 19:32 pet, 26. 11. 2010 Naslov: |
    |
|
|
[latex]\displaystyle $\begin{align*}
D_n & = \left| \begin{array}{rrrrrrr}
0 & 1 & 1 & \ldots & 1 & 1 & 1 \\
-1 & 0 & 1 & \ldots & 1 & 1 & 1 \\
-1 & -1 & 0 & \ldots & 1 & 1 & 1 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
-1 & -1 & -1 & \ldots & 0 & 1 & 1 \\
-1 & -1 & -1 & \ldots & -1 & 0 & 1 \\
-1 & -1 & -1 & \ldots & -1 & -1 & 0 \\
\end{array} \right| \stackrel{(1)}{=} \left| \begin{array}{rrrrrrr}
0 & 1 & 1 & \ldots & 1 & 1 & 1 \\
-1 & -1 & 0 & \ldots & 0 & 0 & 0 \\
-1 & -2 & -1 & \ldots & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
-1 & -2 & -2 & \ldots & -1 & 0 & 0 \\
-1 & -2 & -2 & \ldots & -2 & -1 & 0 \\
-1 & -1 & -1 & \ldots & -1 & -1 & 0 \\
\end{array} \right| \\
& \stackrel{(2)}{=}
(-1)^{n + 1} \left| \begin{array}{rrrrrrr}
-1 & -1 & 0 & \ldots & 0 & 0 & 0 \\
-1 & -2 & -1 & \ldots & 0 & 0 & 0 \\
-1 & -2 & -2 & \ldots & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
-1 & -2 & -2 & \ldots & -2 & -1 & 0 \\
-1 & -2 & -2 & \ldots & -2 & -2 & -1 \\
-1 & -1 & -1 & \ldots & -1 & -1 & -1 \\
\end{array} \right| \\
& \stackrel{(3)}{=}
(-1)^{n + 1} \left| \begin{array}{crrrrrr}
\frac{-1 + (-1)^{n - 1}}{2} & 0 & 0 & \ldots & 0 & 0 & 0 \\
\frac{-1 + (-1)^{n - 2}}{2} & -1 & 0 & \ldots & 0 & 0 & 0 \\
\frac{-1 + (-1)^{n - 3}}{2} & -1 & -1 & \ldots & 0 & 0 & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\
-1 & -1 & -1 & \ldots & -1 & 0 & 0 \\
0 & -1 & -1 & \ldots & -1 & -1 & 0 \\
-1 & -1 & -1 & \ldots & -1 & -1 & -1 \\
\end{array} \right| \\
& = (-1)^{n + 1} \cdot \frac{-1 + (-1)^{n - 1}}{2} \cdot (-1)^{n - 2} = \frac{1 + (-1)^{n}}{2} \end{align*}[/latex]
[latex](1)[/latex] - [latex]i[/latex]-tom retku oduzmemo prvi, [latex]i = 2, \ldots, n - 1[/latex]
[latex](2)[/latex] - Laplace-ov razvoj po zadnjem stupcu
[latex](3)[/latex] - od [latex](n - 1).[/latex] retka oduzmemo [latex]n[/latex]-ti redak, od [latex](n - 2).[/latex] retka oduzmemo [latex](n - 1).[/latex] (novi) redak, ..., od prvog retka oduzmemo drugi redak. Tako se uoči da će se u prvom stupcu izmjenjivati 0 i -1. [latex]\displaystyle \frac{-1 + (-1)^{n}}{2}[/latex] je samo uber-pametan način zapisa toga. Lako se vidi da je [latex]\displaystyle \frac{-1 + (-1)^{n}}{2} = \left\{ \begin{array}{rl}
0, & n\ {\sf paran} \\
-1, & n\ {\sf neparan}
\end{array} \right.[/latex]
Za one kojima je zadnji redak zbunjujući, treba uočiti da vrijedi: [latex](-1)^{n + 1} (-1)^{n - 2} = (-1)^{2 n - 1} = -1[/latex].
Dakle, [latex]D_{2 n} = 1[/latex], a [latex]D_{2 n - 1} = 0[/latex], za svaki [latex]n \in \mathbb{N}[/latex].
Nije mi jasno zašto forumski latex odbija napisati vertikalne točkice. :-k

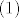 - -  -tom retku oduzmemo prvi, -tom retku oduzmemo prvi, 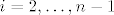
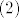 - Laplace-ov razvoj po zadnjem stupcu - Laplace-ov razvoj po zadnjem stupcu
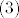 - od - od  retka oduzmemo retka oduzmemo  -ti redak, od -ti redak, od  retka oduzmemo retka oduzmemo  (novi) redak, ..., od prvog retka oduzmemo drugi redak. Tako se uoči da će se u prvom stupcu izmjenjivati 0 i -1. (novi) redak, ..., od prvog retka oduzmemo drugi redak. Tako se uoči da će se u prvom stupcu izmjenjivati 0 i -1. 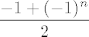 je samo uber-pametan način zapisa toga. Lako se vidi da je je samo uber-pametan način zapisa toga. Lako se vidi da je 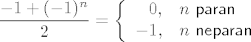
Za one kojima je zadnji redak zbunjujući, treba uočiti da vrijedi: 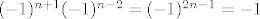 . .
Dakle, 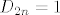 , a , a 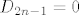 , za svaki , za svaki  . .
Nije mi jasno zašto forumski latex odbija napisati vertikalne točkice. 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
|







