| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
fejky
Forumaš(ica)
Pridružen/a: 23. 06. 2010. (16:53:45)
Postovi: (3D)16
Spol: 
|
 Postano: 22:56 pet, 21. 1. 2011 Naslov: Postano: 22:56 pet, 21. 1. 2011 Naslov: |
    |
|
|
b)
stavimo da je [latex]a_n=1+\sqrt{2}+...+\sqrt[n]{n}, b_n = n[/latex] tada vidimo da mozemo iskoristit stolza jer je [latex]b_n[/latex] neogranicen i rastuci.
pa po stolzu taj limes ([latex]\frac{a_n}{b_n}[/latex]) ako postoji (hvala na ispravci) jednak je [latex]\frac{a_n_+_1-a_n}{b_n_+_1-b_n}[/latex] pa dobijemo [latex]$\lim_{n\to\infty}\frac{\sqrt[n+1]{n+1}-\sqrt[n]{n}}{n+1-n}[/latex] gdje je poznato da je [latex]$\lim_{n\to\infty}\sqrt[n]{n}=\lim_{n\to\infty}\sqrt[n+1]{n+1} = 1 [/latex] i dobijemo kao rijesenje 0. Bar mislim da je tak :D
d) neznam po stolzu ali dal bi se dalo ovako?
[latex]p\,=\,(1+\frac{1}{1})^1\,(1+\frac{1}{2})^2(1+\frac{1}{3})^3...(1+\frac{1}{n})^n[/latex]
Jer je [latex]p\ge1[/latex] znamo da je [latex]\,1\,\le\,\sqrt[n]{p}\,\,[/latex]. Sa druge strane [latex]p\le\,n\cdot(1+\frac{1}{1})[/latex] pa imamo [latex]\sqrt[n]{p}\le\,\sqrt[n]{2n}[/latex].
[latex]\,1\,\le\,\sqrt[n]{p}\,\,\le\,\sqrt[n]{2n}[/latex], pa po tm. o sendvicu i taj limes je 1.
b)
stavimo da je 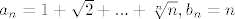 tada vidimo da mozemo iskoristit stolza jer je tada vidimo da mozemo iskoristit stolza jer je 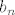 neogranicen i rastuci. neogranicen i rastuci.
pa po stolzu taj limes (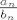 ) ako postoji (hvala na ispravci) jednak je ) ako postoji (hvala na ispravci) jednak je 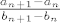 pa dobijemo pa dobijemo 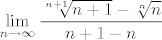 gdje je poznato da je gdje je poznato da je 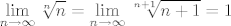 i dobijemo kao rijesenje 0. Bar mislim da je tak i dobijemo kao rijesenje 0. Bar mislim da je tak 
d) neznam po stolzu ali dal bi se dalo ovako?
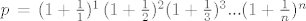
Jer je 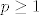 znamo da je znamo da je 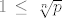 . Sa druge strane . Sa druge strane 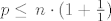 pa imamo pa imamo 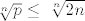 . .
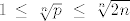 , pa po tm. o sendvicu i taj limes je 1. , pa po tm. o sendvicu i taj limes je 1.
Zadnja promjena: fejky; 23:59 pet, 21. 1. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 0:08 sub, 22. 1. 2011 Naslov: Postano: 0:08 sub, 22. 1. 2011 Naslov: |
    |
|
|
Samo malena opaska, znaci kad koristimo Cesaro-Stolz, AKO postoji limes
[latex] \frac{a_{n+1}+a_n}{b_{n+1}-b_n}=L[/latex], onda postoji i [latex]\frac{a_n}{b_n}[/latex] te je jedak [latex]L[/latex]
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
2.d) U sendvicu imas gresku, u onom koraku kad si zakljucio/la koja bi bila gornja granica. :wink:
Ok vratimo se na zadatak. Znaci uzmemo ln od tog izraza, brojnik rastavimo na pribrojnike, a u nazivniku cijelog izraza imamo samo n. Sada koristimo Cesaro-Stolz, pa je limes jednak [latex]e[/latex]. :)
Posto je zadatak sasvim obican i kratak nakon uzimanja ln-a, nisam pisao korake, no ako nije jasno i trebam napisati, recite. :)
Samo malena opaska, znaci kad koristimo Cesaro-Stolz, AKO postoji limes
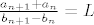 , onda postoji i , onda postoji i 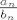 te je jedak te je jedak 
Added after 13 minutes:
2.d) U sendvicu imas gresku, u onom koraku kad si zakljucio/la koja bi bila gornja granica. 
Ok vratimo se na zadatak. Znaci uzmemo ln od tog izraza, brojnik rastavimo na pribrojnike, a u nazivniku cijelog izraza imamo samo n. Sada koristimo Cesaro-Stolz, pa je limes jednak  . . 
Posto je zadatak sasvim obican i kratak nakon uzimanja ln-a, nisam pisao korake, no ako nije jasno i trebam napisati, recite. 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 15:04 sub, 22. 1. 2011 Naslov: Postano: 15:04 sub, 22. 1. 2011 Naslov: |
    |
|
|
[quote="fejky"]b)
stavimo da je [latex]a_n=1+\sqrt{2}+...+\sqrt[n]{n}, b_n = n[/latex] tada vidimo da mozemo iskoristit stolza jer je [latex]b_n[/latex] neogranicen i rastuci.
pa po stolzu taj limes ([latex]\frac{a_n}{b_n}[/latex]) ako postoji (hvala na ispravci) jednak je [latex]\frac{a_n_+_1-a_n}{b_n_+_1-b_n}[/latex] pa dobijemo [latex]$\lim_{n\to\infty}\frac{\sqrt[n+1]{n+1}-\sqrt[n]{n}}{n+1-n}[/latex] gdje je poznato da je [latex]$\lim_{n\to\infty}\sqrt[n]{n}=\lim_{n\to\infty}\sqrt[n+1]{n+1} = 1 [/latex] i dobijemo kao rijesenje 0. Bar mislim da je tak :D
d) neznam po stolzu ali dal bi se dalo ovako?
[latex]p\,=\,(1+\frac{1}{1})^1\,(1+\frac{1}{2})^2(1+\frac{1}{3})^3...(1+\frac{1}{n})^n[/latex]
Jer je [latex]p\ge1[/latex] znamo da je [latex]\,1\,\le\,\sqrt[n]{p}\,\,[/latex]. Sa druge strane [latex]p\le\,n\cdot(1+\frac{1}{1})[/latex] pa imamo [latex]\sqrt[n]{p}\le\,\sqrt[n]{2n}[/latex].
[latex]\,1\,\le\,\sqrt[n]{p}\,\,\le\,\sqrt[n]{2n}[/latex], pa po tm. o sendvicu i taj limes je 1.[/quote]
Rjesenje pod b) je nazalost netocno, rjesili smo ga na satu, greska je gore kod:
lim a_n+1 - a_n -----> to je jednako (n+1)-ti korjen(n+1)= 1
Pa je 1/1= 1.
Ako se razumijemo.
Znaci rjesenje pod d je ln e = 1.
| fejky (napisa): | b)
stavimo da je 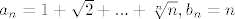 tada vidimo da mozemo iskoristit stolza jer je tada vidimo da mozemo iskoristit stolza jer je 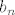 neogranicen i rastuci. neogranicen i rastuci.
pa po stolzu taj limes (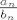 ) ako postoji (hvala na ispravci) jednak je ) ako postoji (hvala na ispravci) jednak je 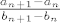 pa dobijemo pa dobijemo 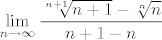 gdje je poznato da je gdje je poznato da je 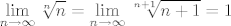 i dobijemo kao rijesenje 0. Bar mislim da je tak i dobijemo kao rijesenje 0. Bar mislim da je tak 
d) neznam po stolzu ali dal bi se dalo ovako?
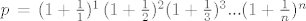
Jer je 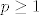 znamo da je znamo da je 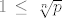 . Sa druge strane . Sa druge strane 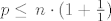 pa imamo pa imamo 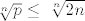 . .
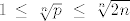 , pa po tm. o sendvicu i taj limes je 1. , pa po tm. o sendvicu i taj limes je 1. |
Rjesenje pod b) je nazalost netocno, rjesili smo ga na satu, greska je gore kod:
lim a_n+1 - a_n -----> to je jednako (n+1)-ti korjen(n+1)= 1
Pa je 1/1= 1.
Ako se razumijemo.
Znaci rjesenje pod d je ln e = 1.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 16:00 sub, 22. 1. 2011 Naslov: Postano: 16:00 sub, 22. 1. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]U tome sto si napisala nema greske, ali zaboravila si da si na pocetku zadatka uzela ln(a_n), pa sad imas ln(a_n)=1 -> a_n=e, nije li tako? :wink:[/quote]
da, da to stoji :D aaa da, znaci gledamo samo limes od a_n. Ockej, jasno mi je.
Tenk ju. :wink:
| Tomislav (napisa): | U tome sto si napisala nema greske, ali zaboravila si da si na pocetku zadatka uzela ln(a_n), pa sad imas ln(a_n)=1 → a_n=e, nije li tako?  |
da, da to stoji  aaa da, znaci gledamo samo limes od a_n. Ockej, jasno mi je. aaa da, znaci gledamo samo limes od a_n. Ockej, jasno mi je.
Tenk ju. 
|
|
| [Vrh] |
|
|








