| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
 Postano: 11:41 čet, 20. 1. 2011 Naslov: duh popravnih kolokvija Postano: 11:41 čet, 20. 1. 2011 Naslov: duh popravnih kolokvija |
    |
|
|
može hint za 3. zadatak popravnog kolokvija 2009. http://web.math.hr/nastava/analiza/kol/ma1-0809-popr.pdf
ne znam kako bi se rastavio taj niz? i što bi s najmanjim cijelom trebalo napraviti?
I ako je itko rješavao zadatke popravnih neka slobodno napiše svoja rješenja pa da uspoređujemo.
evo mojih:[b]2010.[/b]:
1.a) <-besk., -1>; 1.b1) [-1/4(ln 3/2)na kvadrat, ln3ln2; 1.b2) granice za nulu su 2 ili 3, (za -1 zapeh :( ... može i tu hint ak se nekom da) edit: moje rješenje je <2, 3>
2.a)ne znam; 2.b)3;
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
4.a) 1/2; 4.b) 6
[b]2009.[/b]:
1.a)[0,+besk.>; 1.b)4; 1.c)<4,25>
2.a)niz je neomeđen pa nema limes; 2.b)limes je 3
3. ne znam
4.a) -1/2 4.b) 1/9
DALJE ĆEMO VIDIT :P
može hint za 3. zadatak popravnog kolokvija 2009. http://web.math.hr/nastava/analiza/kol/ma1-0809-popr.pdf
ne znam kako bi se rastavio taj niz? i što bi s najmanjim cijelom trebalo napraviti?
I ako je itko rješavao zadatke popravnih neka slobodno napiše svoja rješenja pa da uspoređujemo.
evo mojih:2010.:
1.a) ←besk., -1>; 1.b1) [-1/4(ln 3/2)na kvadrat, ln3ln2; 1.b2) granice za nulu su 2 ili 3, (za -1 zapeh  ... može i tu hint ak se nekom da) edit: moje rješenje je <2, 3> ... može i tu hint ak se nekom da) edit: moje rješenje je <2, 3>
2.a)ne znam; 2.b)3;
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
4.a) 1/2; 4.b) 6
2009.:
1.a)[0,+besk.>; 1.b)4; 1.c)<4,25>
2.a)niz je neomeđen pa nema limes; 2.b)limes je 3
3. ne znam
4.a) -1/2 4.b) 1/9
DALJE ĆEMO VIDIT 
Zadnja promjena: klopka; 17:50 čet, 20. 1. 2011; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 14:04 čet, 20. 1. 2011 Naslov: Postano: 14:04 čet, 20. 1. 2011 Naslov: |
    |
|
|
Evo ja cu rijesiti 2. zadatak 2010. :)
a) Oznacimo taj produkt sa [latex]a_{n}[/latex].
Sada je ocito [latex]0<a_{n}[/latex].
Znamo da je [latex]2^{\frac{1}{2n-1}}>1[/latex], za svaki prirodan broj [latex]n[/latex], pa je sada [latex]\sqrt{2}-2^{\frac{1}{2n-1}}<\sqrt{2}-1[/latex].
Zato je sada [latex]a_{n}<(\sqrt{2}-1)^{n}[/latex]
A limes od [latex](\sqrt{2}-1)^{n}=0[/latex] (zato jer je lim n->inf ([latex]a^n=0[/latex]), gdje je [latex]0<a<1[/latex], pa je prema teoremu o sendvicu limes od [latex]a_{n}=0[/latex] :)
b) Koristimo formulu za sumu geometrijskog niza, pa izraz postaje jednak:
[latex]\frac{3^{\frac{1}{n}}(3^{\frac{n}{n}}-1)}{n(3^{\frac{1}{n}}-1)}[/latex], sad nakon sto iskoristimo da je lim n->inf [latex]\frac{3^{\frac{1}{n}}-1}{\frac{1}{n}}=ln3[/latex] (to nam je nazivnik), a brojnik je jednak [latex]2[/latex] (jer [latex]3^{\frac{1}{n}}->1[/latex]). Konacno je rjesenje dakle: [latex]\frac{2}{ln3}[/latex] :)
Evo i 3. zadatka 2009:
Znaci vrijedi sljedece: [latex] n^{2}+1>2n-1[/latex], za svaki prirodan broj n, i to zato jer je [latex](n-1)^{2}=n^{2}-2n+1>-1[/latex]. Sad je: [latex]1>{\frac{2n-1}{n^2 +1}}>0[/latex], pa je [latex]\lfloor\frac{2n-1}{n^2 +1}}\rfloor=0[/latex]. Sada samo promatramo je li broj n paran ili neparan, pa formiramo 2 slucaja. Ako treba raspisati rjesenje do kraja, reci. :)
Evo ja cu rijesiti 2. zadatak 2010. 
a) Oznacimo taj produkt sa 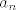 . .
Sada je ocito  . .
Znamo da je 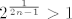 , za svaki prirodan broj , za svaki prirodan broj  , pa je sada , pa je sada 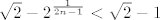 . .
Zato je sada 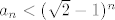
A limes od 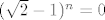 (zato jer je lim n→inf ( (zato jer je lim n→inf ( ), gdje je ), gdje je 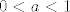 , pa je prema teoremu o sendvicu limes od , pa je prema teoremu o sendvicu limes od 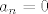 
b) Koristimo formulu za sumu geometrijskog niza, pa izraz postaje jednak:
 , sad nakon sto iskoristimo da je lim n→inf , sad nakon sto iskoristimo da je lim n→inf  (to nam je nazivnik), a brojnik je jednak (to nam je nazivnik), a brojnik je jednak  (jer (jer 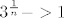 ). Konacno je rjesenje dakle: ). Konacno je rjesenje dakle: 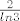 
Evo i 3. zadatka 2009:
Znaci vrijedi sljedece: 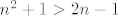 , za svaki prirodan broj n, i to zato jer je , za svaki prirodan broj n, i to zato jer je  . Sad je: . Sad je: 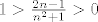 , pa je , pa je  . Sada samo promatramo je li broj n paran ili neparan, pa formiramo 2 slucaja. Ako treba raspisati rjesenje do kraja, reci. . Sada samo promatramo je li broj n paran ili neparan, pa formiramo 2 slucaja. Ako treba raspisati rjesenje do kraja, reci. 
|
|
| [Vrh] |
|
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 16:23 čet, 20. 1. 2011 Naslov: Postano: 16:23 čet, 20. 1. 2011 Naslov: |
    |
|
|
[quote="klopka"]puno ti hvala :) , slijedi jedna pohvala od mene!
Riješenje trećeg je infS=-1, sup S=1.
Samo me malo ovaj 2.b) iz 2010. zbunio, jer ja sam preko Stolzovog teorema (jer nazivnik ide u beskonačno)dobila rezultat 3. :?[/quote]
Vjerujem da slutim gdje je problem :). Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je [latex]a_{n+1}[/latex] brojnik s jos jednim dodatnim clanom, i to [latex]3^{\frac{n+1}{n}}[/latex]? Ako je tako, greska je u tome sto ti je [latex]a_{n+1}=3^{1/(n+1)}+3^{2/(n+2)}+...+3^{(n+1)/(n+1)}[/latex], a ne [latex]3^{1/n}+3^{2/n}+...+3^{n/n}+3^{(n+1)/n}[/latex]. :)
Ako nije problem u ovome sto sam napisao, ispisi svoj postupak pa cemo vidjeti :)
| klopka (napisa): | puno ti hvala  , slijedi jedna pohvala od mene! , slijedi jedna pohvala od mene!
Riješenje trećeg je infS=-1, sup S=1.
Samo me malo ovaj 2.b) iz 2010. zbunio, jer ja sam preko Stolzovog teorema (jer nazivnik ide u beskonačno)dobila rezultat 3.  |
Vjerujem da slutim gdje je problem  . Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je . Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je 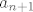 brojnik s jos jednim dodatnim clanom, i to brojnik s jos jednim dodatnim clanom, i to 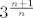 ? Ako je tako, greska je u tome sto ti je ? Ako je tako, greska je u tome sto ti je  , a ne , a ne  . . 
Ako nije problem u ovome sto sam napisao, ispisi svoj postupak pa cemo vidjeti 
|
|
| [Vrh] |
|
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
 Postano: 17:45 čet, 20. 1. 2011 Naslov: Postano: 17:45 čet, 20. 1. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]
Vjerujem da slutim gdje je problem :). Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je [latex]a_{n+1}[/latex] brojnik s jos jednim dodatnim clanom, i to [latex]3^{\frac{n+1}{n}}[/latex]? Ako je tako, greska je u tome sto ti je [latex]a_{n+1}=3^{1/(n+1)}+3^{2/(n+2)}+...+3^{(n+1)/(n+1)}[/latex], a ne [latex]3^{1/n}+3^{2/n}+...+3^{n/n}+3^{(n+1)/n}[/latex]. :)
Ako nije problem u ovome sto sam napisao, ispisi svoj postupak pa cemo vidjeti :)[/quote]
da valjda tako nekako... ja sam dobila da mi je cijeli brojnik [latex]3^{(n+1)/(n+1)}[/latex]. :oops:
Kako da odredim onda brojnik tj. [latex]a_{n+1} - a_{n}[/latex] ?
| Tomislav (napisa): |
Vjerujem da slutim gdje je problem  . Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je . Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je 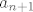 brojnik s jos jednim dodatnim clanom, i to brojnik s jos jednim dodatnim clanom, i to 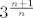 ? Ako je tako, greska je u tome sto ti je ? Ako je tako, greska je u tome sto ti je  , a ne , a ne  . . 
Ako nije problem u ovome sto sam napisao, ispisi svoj postupak pa cemo vidjeti  |
da valjda tako nekako... ja sam dobila da mi je cijeli brojnik  . . 
Kako da odredim onda brojnik tj.  ? ?
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 17:53 čet, 20. 1. 2011 Naslov: Postano: 17:53 čet, 20. 1. 2011 Naslov: |
    |
|
|
Rješenje koristeci geometrijski niz je puno jednostavnije, no ako bas zelis Cesaro-Stolz, ok, makar se to opet svodi na koristenje geometrijskog niza, pa je u ovom slucaju to samo nepotrebna komplikacija (znaci samo izracunaj sumu geometrijskog niza [latex]a_{n+1}[/latex], pa zatim [latex]a_{n}[/latex] te iz naravno oduzmes. :wink: .
Rješenje koristeci geometrijski niz je puno jednostavnije, no ako bas zelis Cesaro-Stolz, ok, makar se to opet svodi na koristenje geometrijskog niza, pa je u ovom slucaju to samo nepotrebna komplikacija (znaci samo izracunaj sumu geometrijskog niza 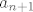 , pa zatim , pa zatim 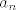 te iz naravno oduzmes. te iz naravno oduzmes.  . .
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 15:23 pet, 21. 1. 2011 Naslov: Re: duh popravnih kolokvija Postano: 15:23 pet, 21. 1. 2011 Naslov: Re: duh popravnih kolokvija |
    |
|
|
[quote="klopka"]
[b]2009.[/b]:
1.a)[0,+besk.>; 1.b)4; 1.c)<4,25>
2.a)niz je neomeđen pa nema limes; 2.b)limes je 3
3. ne znam
4.a) -1/2 4.b) 1/9
DALJE ĆEMO VIDIT :P[/quote]
Porvjeravam pod 1. zad:
a) OK
b) meni ispada f(<0,25>)= <-4, 12>
c) a tu mi ispada f^-1( <0,3>)= <4,9> U <25, 36>
Mozes mi reci kak si dobila ti svoje rezultate i molila bih da jos netko pregleda.
[size=9][color=#999999]Added after 59 minutes:[/color][/size]
[quote="frutabella"][quote="klopka"]
[b]2009.[/b]:
1.a)[0,+besk.>; 1.b)4; 1.c)<4,25>
2.a)niz je neomeđen pa nema limes; 2.b)limes je 3
3. ne znam
4.a) -1/2 4.b) 1/9
DALJE ĆEMO VIDIT :P[/quote]
Porvjeravam pod 1. zad:
a) OK
b) meni ispada f(<0,25>)= <-4, 12>
c) a tu mi ispada f^-1( <0,3>)= <4,9> U <25, 36>
Mozes mi reci kak si dobila ti svoje rezultate i molila bih da jos netko pregleda.[/quote]
Pod 4. zadatkom:
a) ako ti je A=1, B=+besk (ma da ja nisam skroz ziher zasto bi tu moglo biti +besk, al ne mogu nikako nastimat pa da ispadne 1)
onda vrijedi ona formula sa e^lim ... i dobijes gore limes -1/2, al si mozda zaboravila staviti jos na e, pa je to e^(-1/2)= 1/korjen(e)
| klopka (napisa): |
2009.:
1.a)[0,+besk.>; 1.b)4; 1.c)<4,25>
2.a)niz je neomeđen pa nema limes; 2.b)limes je 3
3. ne znam
4.a) -1/2 4.b) 1/9
DALJE ĆEMO VIDIT  |
Porvjeravam pod 1. zad:
a) OK
b) meni ispada f(<0,25>)= ←4, 12>
c) a tu mi ispada f^-1( <0,3>)= <4,9> U <25, 36>
Mozes mi reci kak si dobila ti svoje rezultate i molila bih da jos netko pregleda.
Added after 59 minutes:
| frutabella (napisa): | | klopka (napisa): |
2009.:
1.a)[0,+besk.>; 1.b)4; 1.c)<4,25>
2.a)niz je neomeđen pa nema limes; 2.b)limes je 3
3. ne znam
4.a) -1/2 4.b) 1/9
DALJE ĆEMO VIDIT  |
Porvjeravam pod 1. zad:
a) OK
b) meni ispada f(<0,25>)= ←4, 12>
c) a tu mi ispada f^-1( <0,3>)= <4,9> U <25, 36>
Mozes mi reci kak si dobila ti svoje rezultate i molila bih da jos netko pregleda. |
Pod 4. zadatkom:
a) ako ti je A=1, B=+besk (ma da ja nisam skroz ziher zasto bi tu moglo biti +besk, al ne mogu nikako nastimat pa da ispadne 1)
onda vrijedi ona formula sa e^lim ... i dobijes gore limes -1/2, al si mozda zaboravila staviti jos na e, pa je to e^(-1/2)= 1/korjen(e)
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 15:54 sub, 22. 1. 2011 Naslov: Postano: 15:54 sub, 22. 1. 2011 Naslov: |
    |
|
|
[quote="klopka"]ova rješenja šta si napisala za 2009. 1b) i 1c) su točna, ne znam kako sam to uspila napisati?! sad gledam u riješenja i ista su mi kao tebi :)
[quote="frutabella"]Pod 4.b) meni ispada 1/4.
U brojniku je kvadrat razlike, i to pomnozim sa suprotnim znakom na kvadrat,
znaci sa (3.korrjen(x)+1)^2.[/quote]
u tom zadatku sam brojnik napisala isto kao kvadrat razlike. Pošto ti je nazivnik isto neki-izraz na kvadrat, možeš sve stavit kao razlomak na kvadrat. Sada nazivnik riješiš po razlici kubova (stavi se 3.korijen iz 3 na 3. minus 1 pa onda vidiš kako bi izgledala ta razlika kubova). skrati se brojnik i prva zagrada nazivnika pa dobiš jedan kroz 3. korijen iz x sve na kvadrat plus 3. korijen iz x plus 1. pa to sve na kvadrat.......... probaj si sve ovo raspisati jer ne znam još koristiti latex pa će ti biti jasnije![/quote]
Jeste, jeste, u pravu si, jesam glupa, pa naravno da ne ide onaj moj slucaj jer je 3.korjen. Skontala sam odmah sto si htjela, hvala ti. :D
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
[quote="klopka"][quote="Tomislav"]
Vjerujem da slutim gdje je problem :). Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je [latex]a_{n+1}[/latex] brojnik s jos jednim dodatnim clanom, i to [latex]3^{\frac{n+1}{n}}[/latex]? Ako je tako, greska je u tome sto ti je [latex]a_{n+1}=3^{1/(n+1)}+3^{2/(n+2)}+...+3^{(n+1)/(n+1)}[/latex], a ne [latex]3^{1/n}+3^{2/n}+...+3^{n/n}+3^{(n+1)/n}[/latex]. :)
Ako nije problem u ovome sto sam napisao, ispisi svoj postupak pa cemo vidjeti :)[/quote]
da valjda tako nekako... ja sam dobila da mi je cijeli brojnik [latex]3^{(n+1)/(n+1)}[/latex]. :oops:
Kako da odredim onda brojnik tj. [latex]a_{n+1} - a_{n}[/latex] ?[/quote]
Joj, meni opet nije bas sasvim jasno, ako stolza upotrijebimo zar nije onda:
3 ^(1/n) + 3^(2/n) + ... + 3^(n/n) + 3^([n+1]/[n+1]) = a_n+1
pa kad od toga oduzmem a_n, to je jedanko 3^([n+1]/[n+1]), pa sad od toga limes?
| klopka (napisa): | ova rješenja šta si napisala za 2009. 1b) i 1c) su točna, ne znam kako sam to uspila napisati?! sad gledam u riješenja i ista su mi kao tebi 
| frutabella (napisa): | Pod 4.b) meni ispada 1/4.
U brojniku je kvadrat razlike, i to pomnozim sa suprotnim znakom na kvadrat,
znaci sa (3.korrjen(x)+1)^2. |
u tom zadatku sam brojnik napisala isto kao kvadrat razlike. Pošto ti je nazivnik isto neki-izraz na kvadrat, možeš sve stavit kao razlomak na kvadrat. Sada nazivnik riješiš po razlici kubova (stavi se 3.korijen iz 3 na 3. minus 1 pa onda vidiš kako bi izgledala ta razlika kubova). skrati se brojnik i prva zagrada nazivnika pa dobiš jedan kroz 3. korijen iz x sve na kvadrat plus 3. korijen iz x plus 1. pa to sve na kvadrat.......... probaj si sve ovo raspisati jer ne znam još koristiti latex pa će ti biti jasnije! |
Jeste, jeste, u pravu si, jesam glupa, pa naravno da ne ide onaj moj slucaj jer je 3.korjen. Skontala sam odmah sto si htjela, hvala ti. 
Added after 11 minutes:
| klopka (napisa): | | Tomislav (napisa): |
Vjerujem da slutim gdje je problem  . Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je . Naime, ti si vjerojatno oznacila da ti je cijeli brojnik jednak a_n (n-ti clan niza). Onda si stavila da ti je 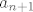 brojnik s jos jednim dodatnim clanom, i to brojnik s jos jednim dodatnim clanom, i to 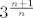 ? Ako je tako, greska je u tome sto ti je ? Ako je tako, greska je u tome sto ti je  , a ne , a ne  . . 
Ako nije problem u ovome sto sam napisao, ispisi svoj postupak pa cemo vidjeti  |
da valjda tako nekako... ja sam dobila da mi je cijeli brojnik  . . 
Kako da odredim onda brojnik tj.  ? ? |
Joj, meni opet nije bas sasvim jasno, ako stolza upotrijebimo zar nije onda:
3 ^(1/n) + 3^(2/n) + ... + 3^(n/n) + 3^([n+1]/[n+1]) = a_n+1
pa kad od toga oduzmem a_n, to je jedanko 3^([n+1]/[n+1]), pa sad od toga limes?
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 16:30 sub, 22. 1. 2011 Naslov: Re: duh popravnih kolokvija Postano: 16:30 sub, 22. 1. 2011 Naslov: Re: duh popravnih kolokvija |
    |
|
|
[quote="klopka"]
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
[/quote]
inf i meni ispada isti, al supremum mi ne ide u 3, vec u 6, ako se ne varam supA=2 (za n iz N)
supB=3 (za m iz N) pa to dvoje kad se pomnozi...6 (a mnozi se jer su oba skupa su u intervalu [0, +besk>
| klopka (napisa): |
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
|
inf i meni ispada isti, al supremum mi ne ide u 3, vec u 6, ako se ne varam supA=2 (za n iz N)
supB=3 (za m iz N) pa to dvoje kad se pomnozi...6 (a mnozi se jer su oba skupa su u intervalu [0, +besk>
|
|
| [Vrh] |
|
lalala5
Forumaš(ica)

Pridružen/a: 06. 10. 2010. (17:54:28)
Postovi: (3C)16
|
|
| [Vrh] |
|
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
 Postano: 17:39 sub, 22. 1. 2011 Naslov: Re: duh popravnih kolokvija Postano: 17:39 sub, 22. 1. 2011 Naslov: Re: duh popravnih kolokvija |
    |
|
|
[quote="frutabella"][quote="klopka"]
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
[/quote]
inf i meni ispada isti, al supremum mi ne ide u 3, vec u 6, ako se ne varam supA=2 (za n iz N)
supB=3 (za m iz N) pa to dvoje kad se pomnozi...6 (a mnozi se jer su oba skupa su u intervalu [0, +besk>[/quote]
hmm ako se množe riješenja skupova A i B onda su mi kriva riješenja...
znači ovako:
skup A ima član [latex]a_n[/latex] jednak [latex]\frac{(2n-1)}{(n+1)}[/latex] ...to je rastući niz pa je inf A=a_1=1/2; supA=lim(kada n->besk.) a_n=2
skup B ima član [latex]b_n[/latex] jednak [latex]\frac{(2+m)}{3m-2}[/latex] ...to je rastući niz pa je inf B=b_1=3; supB=lim(kada m->besk.) b_m=1/3.
skup S(=A*B) je padajući pa će njegov inf biti jednak (ako je ono množenje rješenja kako si rekla ispravno) supA*supB;
a supS=infA*infB. Ako netko zna je li ovo krivo/dobro neka se izjasni.
Ako je dobro--> konačno rj.: sup S=logaritam po bazi 1/6 od 3/2; inf S=logaritam po bazi 1/6 od 2/3
| frutabella (napisa): | | klopka (napisa): |
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
|
inf i meni ispada isti, al supremum mi ne ide u 3, vec u 6, ako se ne varam supA=2 (za n iz N)
supB=3 (za m iz N) pa to dvoje kad se pomnozi...6 (a mnozi se jer su oba skupa su u intervalu [0, +besk> |
hmm ako se množe riješenja skupova A i B onda su mi kriva riješenja...
znači ovako:
skup A ima član 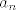 jednak jednak 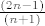 ...to je rastući niz pa je inf A=a_1=1/2; supA=lim(kada n→besk.) a_n=2 ...to je rastući niz pa je inf A=a_1=1/2; supA=lim(kada n→besk.) a_n=2
skup B ima član 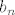 jednak jednak 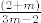 ...to je rastući niz pa je inf B=b_1=3; supB=lim(kada m→besk.) b_m=1/3. ...to je rastući niz pa je inf B=b_1=3; supB=lim(kada m→besk.) b_m=1/3.
skup S(=A*B) je padajući pa će njegov inf biti jednak (ako je ono množenje rješenja kako si rekla ispravno) supA*supB;
a supS=infA*infB. Ako netko zna je li ovo krivo/dobro neka se izjasni.
Ako je dobro→ konačno rj.: sup S=logaritam po bazi 1/6 od 3/2; inf S=logaritam po bazi 1/6 od 2/3
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:28 sub, 22. 1. 2011 Naslov: Re: duh popravnih kolokvija Postano: 18:28 sub, 22. 1. 2011 Naslov: Re: duh popravnih kolokvija |
    |
|
|
[quote="Tomislav"]Pa kad bi vrijedilo to sto si napisala, onda bi limes na kraju bio jednak 3, nije li tako? :). A limes nije jednak 3, tako da ovaj korak sto si napisala nije dobar :wink:[/quote]
Pa kako onda ide stolz... :cry: na tom zadatku...ako mozes malo detaljnije objasnit...
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
[quote="klopka"][quote="frutabella"][quote="klopka"]
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
[/quote]
inf i meni ispada isti, al supremum mi ne ide u 3, vec u 6, ako se ne varam supA=2 (za n iz N)
supB=3 (za m iz N) pa to dvoje kad se pomnozi...6 (a mnozi se jer su oba skupa su u intervalu [0, +besk>[/quote]
hmm ako se množe riješenja skupova A i B onda su mi kriva riješenja...
znači ovako:
skup A ima član [latex]a_n[/latex] jednak [latex]\frac{(2n-1)}{(n+1)}[/latex] ...to je rastući niz pa je inf A=a_1=1/2; supA=lim(kada n->besk.) a_n=2
skup B ima član [latex]b_n[/latex] jednak [latex]\frac{(2+m)}{3m-2}[/latex] ...to je rastući niz pa je inf B=b_1=3; supB=lim(kada m->besk.) b_m=1/3.
skup S(=A*B) je padajući pa će njegov inf biti jednak (ako je ono množenje rješenja kako si rekla ispravno) supA*supB;
a supS=infA*infB. Ako netko zna je li ovo krivo/dobro neka se izjasni.
Ako je dobro--> konačno rj.: sup S=logaritam po bazi 1/6 od 3/2; inf S=logaritam po bazi 1/6 od 2/3[/quote]
Ako se ne varam, a ja mislim da ne, niz b_n je padajuci, pa je supB=b_1=3, a infB=1/3
Da, u pravu si za umnozak, posto je padajuca funkcija supS je umnozak infimuma i obrnuto, pa to onda iznosi
supS= log 1/6 (1/6) = a to je ili -1 ili 1, sad se ne mogu sjetit, kad potencija iz baze prelazi pred cijeli log, znam da ide reciprocna vrijednost, a da li se i predznak mijenja? hmm...
infS= log 1/6 (6) = i to opet ili 1 ili -1
| Tomislav (napisa): | Pa kad bi vrijedilo to sto si napisala, onda bi limes na kraju bio jednak 3, nije li tako?  . A limes nije jednak 3, tako da ovaj korak sto si napisala nije dobar . A limes nije jednak 3, tako da ovaj korak sto si napisala nije dobar  |
Pa kako onda ide stolz...  na tom zadatku...ako mozes malo detaljnije objasnit... na tom zadatku...ako mozes malo detaljnije objasnit...
Added after 11 minutes:
| klopka (napisa): | | frutabella (napisa): | | klopka (napisa): |
3.) inf S=logaritam po bazi 1/6 od 2, sup S= logaritam po bazi 1/6 3
|
inf i meni ispada isti, al supremum mi ne ide u 3, vec u 6, ako se ne varam supA=2 (za n iz N)
supB=3 (za m iz N) pa to dvoje kad se pomnozi...6 (a mnozi se jer su oba skupa su u intervalu [0, +besk> |
hmm ako se množe riješenja skupova A i B onda su mi kriva riješenja...
znači ovako:
skup A ima član 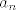 jednak jednak 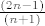 ...to je rastući niz pa je inf A=a_1=1/2; supA=lim(kada n→besk.) a_n=2 ...to je rastući niz pa je inf A=a_1=1/2; supA=lim(kada n→besk.) a_n=2
skup B ima član 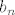 jednak jednak 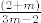 ...to je rastući niz pa je inf B=b_1=3; supB=lim(kada m→besk.) b_m=1/3. ...to je rastući niz pa je inf B=b_1=3; supB=lim(kada m→besk.) b_m=1/3.
skup S(=A*B) je padajući pa će njegov inf biti jednak (ako je ono množenje rješenja kako si rekla ispravno) supA*supB;
a supS=infA*infB. Ako netko zna je li ovo krivo/dobro neka se izjasni.
Ako je dobro→ konačno rj.: sup S=logaritam po bazi 1/6 od 3/2; inf S=logaritam po bazi 1/6 od 2/3 |
Ako se ne varam, a ja mislim da ne, niz b_n je padajuci, pa je supB=b_1=3, a infB=1/3
Da, u pravu si za umnozak, posto je padajuca funkcija supS je umnozak infimuma i obrnuto, pa to onda iznosi
supS= log 1/6 (1/6) = a to je ili -1 ili 1, sad se ne mogu sjetit, kad potencija iz baze prelazi pred cijeli log, znam da ide reciprocna vrijednost, a da li se i predznak mijenja? hmm...
infS= log 1/6 (6) = i to opet ili 1 ili -1
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
lalala5
Forumaš(ica)

Pridružen/a: 06. 10. 2010. (17:54:28)
Postovi: (3C)16
|
|
| [Vrh] |
|
wannaknow
Forumaš(ica)
Pridružen/a: 07. 09. 2010. (16:38:49)
Postovi: (2C)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:18 ned, 23. 1. 2011 Naslov: Postano: 14:18 ned, 23. 1. 2011 Naslov: |
    |
|
|
Ovo su, oprostit ćeš, zbilja lagani zadaci :P, tako da ću dati neki hint za njih, a onda ti probaj dalje, pa pitaj ako će trebati:
1. Podijeli i brojnik i nazivnik s [latex]5^n[/latex]: brojnik će ići u [latex]-1[/latex], a nazivnik u [latex]1[/latex] (tu bi te eventualno moglo mučiti zašto [latex]\displaystyle\frac{\sqrt{n^6-3n}}{5^n}\to 0[/latex], ali to dosta jasno stoji iz teorema o sendviču, s [latex]0\leq \sqrt{n^6-3n}\leq n^3[/latex]).
2. Da uzmemo najjednostavnije rješenje (može i direktnije, ali ne znam jeste li spomenuli/pokazivali da [latex]\displaystyle (1-\frac{1}{n})^n\to \frac{1}{e}[/latex]), gledaj limes od recipročnog niza: [latex]\displaystyle(\frac{n+3}{n+2})^{n+4}[/latex]. Tada stvar izgleda kao [latex]\displaystyle (1+\frac{1}{n+2})^{n+4}[/latex]. E, sad, znaš limes od [latex]\displaystyle (1+\frac{1}{n+2})^{n+2}[/latex], pa je to u biti to: još samo trebaš pomnožiti s [latex]\displaystyle (1+\frac{1}{n+2})^2[/latex], a za to također znaš u što konvergira. :)
3. Čuj, tu ne znam imaš li grešku u zadatku ili nešto. Naime, [latex]n[/latex] se uopće ne spominje, a [latex]x\to +\infty[/latex] ne bi imalo smisla jer onda logaritam u nazivniku uopće ne mora biti definiran. Ako [latex]x\to 0[/latex], to možda ima smisla. :D Podijeli i brojnik i nazivnik s [latex]x^2[/latex]. Brojnik će ići u [latex]2[/latex], a nazivnik je [latex]\displaystyle\frac{\ln(\cos x)}{x^2}[/latex]. Sad iskoristi da [latex]x\to 0[/latex], a [latex]\displaystyle\frac{\ln(\cos x)}{x^2}=\frac{\ln(1+(\cos (x) -1))}{\cos (x) -1}\cdot\frac{\cos (x) -1}{x^2}[/latex], pa si gotova. :)
4. Podijeli i brojnik i nazivnik s [latex]5^n[/latex] i stvar dosta jasno ide u [latex]0/1=0[/latex].
Mislim, čisto jedan generalni savjet, ako smijem - ovaj prvi i četvrti se zapravo svode na to da shvatiš koji je "najjači" član u brojniku, a koji u nazivniku i da ih onda usporediš. Naravno, to što kažem je vrlo neprecizno i ne može se priznati kao legalno rješenje :D, ali na to se svodi: u četvrtom brojnik za velike [latex]n[/latex] "izgleda kao" [latex]3^n[/latex], a nazivnik kao [latex]5^n[/latex]. Kako [latex]3^n[/latex] nije ni do koljena velikom [latex]5^n[/latex], zaključujemo da će rezultat biti [latex]0[/latex]. [url=http://degiorgi.math.hr/forum/viewtopic.php?p=128424#128424]Tu[/url] sam svojedobno to objašnjavao u malo više detalja. :)
Ovo su, oprostit ćeš, zbilja lagani zadaci  , tako da ću dati neki hint za njih, a onda ti probaj dalje, pa pitaj ako će trebati: , tako da ću dati neki hint za njih, a onda ti probaj dalje, pa pitaj ako će trebati:
1. Podijeli i brojnik i nazivnik s 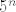 : brojnik će ići u : brojnik će ići u  , a nazivnik u , a nazivnik u  (tu bi te eventualno moglo mučiti zašto (tu bi te eventualno moglo mučiti zašto 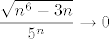 , ali to dosta jasno stoji iz teorema o sendviču, s , ali to dosta jasno stoji iz teorema o sendviču, s  ). ).
2. Da uzmemo najjednostavnije rješenje (može i direktnije, ali ne znam jeste li spomenuli/pokazivali da  ), gledaj limes od recipročnog niza: ), gledaj limes od recipročnog niza:  . Tada stvar izgleda kao . Tada stvar izgleda kao  . E, sad, znaš limes od . E, sad, znaš limes od  , pa je to u biti to: još samo trebaš pomnožiti s , pa je to u biti to: još samo trebaš pomnožiti s  , a za to također znaš u što konvergira. , a za to također znaš u što konvergira. 
3. Čuj, tu ne znam imaš li grešku u zadatku ili nešto. Naime,  se uopće ne spominje, a se uopće ne spominje, a 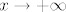 ne bi imalo smisla jer onda logaritam u nazivniku uopće ne mora biti definiran. Ako ne bi imalo smisla jer onda logaritam u nazivniku uopće ne mora biti definiran. Ako 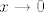 , to možda ima smisla. , to možda ima smisla.  Podijeli i brojnik i nazivnik s Podijeli i brojnik i nazivnik s 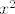 . Brojnik će ići u . Brojnik će ići u  , a nazivnik je , a nazivnik je 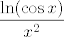 . Sad iskoristi da . Sad iskoristi da 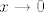 , a , a 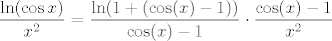 , pa si gotova. , pa si gotova. 
4. Podijeli i brojnik i nazivnik s 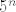 i stvar dosta jasno ide u i stvar dosta jasno ide u 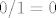 . .
Mislim, čisto jedan generalni savjet, ako smijem - ovaj prvi i četvrti se zapravo svode na to da shvatiš koji je "najjači" član u brojniku, a koji u nazivniku i da ih onda usporediš. Naravno, to što kažem je vrlo neprecizno i ne može se priznati kao legalno rješenje  , ali na to se svodi: u četvrtom brojnik za velike , ali na to se svodi: u četvrtom brojnik za velike  "izgleda kao" "izgleda kao"  , a nazivnik kao , a nazivnik kao 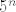 . Kako . Kako  nije ni do koljena velikom nije ni do koljena velikom 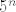 , zaključujemo da će rezultat biti , zaključujemo da će rezultat biti  . Tu sam svojedobno to objašnjavao u malo više detalja. . Tu sam svojedobno to objašnjavao u malo više detalja. 
|
|
| [Vrh] |
|
wannaknow
Forumaš(ica)
Pridružen/a: 07. 09. 2010. (16:38:49)
Postovi: (2C)16
|
|
| [Vrh] |
|
|









