|
Umm, jel možda misliš na osam točaka spomenutih [url=http://web.math.hr/nastava/analiza/files/ch1_9.pdf]tu[/url]?
Ako da, dosta je to posla :D Ajde onda reci kako ti funkcija izgleda - je li [latex]\displaystyle\ln (\frac{2x-1}{3x+2})[/latex] ili [latex]\displaystyle\frac{\ln(2x-1)}{3x+2}[/latex]?
Pretpostavljam da se radi o prvoj opciji: u tom slučaju, za prvu točku (određivanje domene) moraš imati [latex]x\neq -2/3[/latex] i [latex]\displaystyle\frac{2x-1}{3x+2}>0[/latex]. Nije teško pokazati (pitaj ako treba pomoć) da to stoji za [latex]x>1/2[/latex] i za [latex]x<-2/3[/latex].
Lako se vidi da funkcija nije ni parna ni neparna ([latex]f(1)=\displaystyle\ln(\frac{1}{5})[/latex], a [latex]f(1)=\ln 3[/latex]). Nadalje, ona nije ni periodična (ako periodičnost i parnost/neparnost imaju uopće smisla na ovakvoj "kljastoj" domeni): naime, možeš pokazati (ponovno, reci ako treba pomoći) da je [latex]f[/latex] strogo rastuća na [latex]\langle 0.5, +\infty\rangle[/latex].
Naravno (jer se radi o kompoziciji i kvocijentu elementarnih funkcija), naša je funkcija neprekidna svugdje gdje je definirana. Nultočke joj je lagano naći: naprosto riješi [latex]\displaystyle\ln (\frac{2x-1}{3x+2})=0[/latex] iz čega dobivaš [latex]x=-3[/latex]. Što se monotonosti i ekstrema tiče, funkcija je strogo rastuća i na "lijevoj" poddomeni, kao i na "desnoj" (to dokažeš lako, pitaj ako treba :)). Dakle, na lijevoj poddomeni je supremum [latex]\displaystyle\lim_{x\to (-2/3)-} f(x)=+\infty[/latex], a infimum [latex]\displaystyle\lim_{x\to -\infty} f(x)=\ln(\frac{2}{3})[/latex]. Na desnoj poddomeni je infimum [latex]\displaystyle\lim_{x\to (1/2)+} f(x)=-\infty[/latex], a supremum [latex]\displaystyle\lim_{x\to +\infty} f(x)=\ln(\frac{2}{3})[/latex].
Sad smo odredili zapravo i asimptote: vertikalne (iako, samo "jednostrane", ne znam jeste li to smatrali pravim vertikalnima) su [latex]x=1/2[/latex] i [latex]x=-2/3[/latex], a horizontalna je [latex]y=\displaystyle\ln(\frac{2}{3})[/latex].
Još trebaš odrediti intervale konveksnosti i konkavnosti, a za tako nešto trebaš dva puta derivirati funkciju. :D Naravno, to se nikome normalnome ne da, ali [url=http://www.wolframalpha.com/input/?i=ln%28%282x-1%29%2F%283x%2B2%29%29%27%27]navodno[/url] je druga derivacija [latex]\displaystyle -\frac{7(12x+1)}{(2x-1)^2(3x+2)^2}[/latex], što bi značilo da u domeni nema infleksija, a da je na lijevoj poddomeni funkcija konveksna, a na desnoj konkavna.
Što se pak [url=http://www.wolframalpha.com/input/?i=ln%28%282x-1%29%2F%283x%2B2%29%29]grafa[/url] tiče, tu ne mogu biti od velike pomoći - sve korisne informacije zapravo imaš gore. :)
Evo, nisam bio baš detaljan, ali s takvim zadatkom... tko bi bio. :P
Umm, jel možda misliš na osam točaka spomenutih tu?
Ako da, dosta je to posla  Ajde onda reci kako ti funkcija izgleda - je li Ajde onda reci kako ti funkcija izgleda - je li 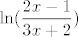 ili ili 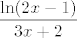 ? ?
Pretpostavljam da se radi o prvoj opciji: u tom slučaju, za prvu točku (određivanje domene) moraš imati 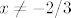 i i 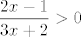 . Nije teško pokazati (pitaj ako treba pomoć) da to stoji za . Nije teško pokazati (pitaj ako treba pomoć) da to stoji za 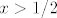 i za i za 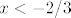 . .
Lako se vidi da funkcija nije ni parna ni neparna (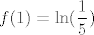 , a , a 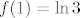 ). Nadalje, ona nije ni periodična (ako periodičnost i parnost/neparnost imaju uopće smisla na ovakvoj "kljastoj" domeni): naime, možeš pokazati (ponovno, reci ako treba pomoći) da je ). Nadalje, ona nije ni periodična (ako periodičnost i parnost/neparnost imaju uopće smisla na ovakvoj "kljastoj" domeni): naime, možeš pokazati (ponovno, reci ako treba pomoći) da je  strogo rastuća na strogo rastuća na 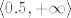 . .
Naravno (jer se radi o kompoziciji i kvocijentu elementarnih funkcija), naša je funkcija neprekidna svugdje gdje je definirana. Nultočke joj je lagano naći: naprosto riješi 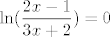 iz čega dobivaš iz čega dobivaš  . Što se monotonosti i ekstrema tiče, funkcija je strogo rastuća i na "lijevoj" poddomeni, kao i na "desnoj" (to dokažeš lako, pitaj ako treba . Što se monotonosti i ekstrema tiče, funkcija je strogo rastuća i na "lijevoj" poddomeni, kao i na "desnoj" (to dokažeš lako, pitaj ako treba  ). Dakle, na lijevoj poddomeni je supremum ). Dakle, na lijevoj poddomeni je supremum 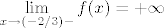 , a infimum , a infimum 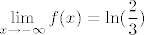 . Na desnoj poddomeni je infimum . Na desnoj poddomeni je infimum 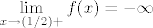 , a supremum , a supremum 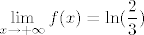 . .
Sad smo odredili zapravo i asimptote: vertikalne (iako, samo "jednostrane", ne znam jeste li to smatrali pravim vertikalnima) su 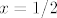 i i 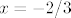 , a horizontalna je , a horizontalna je 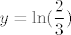 . .
Još trebaš odrediti intervale konveksnosti i konkavnosti, a za tako nešto trebaš dva puta derivirati funkciju.  Naravno, to se nikome normalnome ne da, ali navodno je druga derivacija Naravno, to se nikome normalnome ne da, ali navodno je druga derivacija 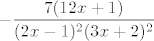 , što bi značilo da u domeni nema infleksija, a da je na lijevoj poddomeni funkcija konveksna, a na desnoj konkavna. , što bi značilo da u domeni nema infleksija, a da je na lijevoj poddomeni funkcija konveksna, a na desnoj konkavna.
Što se pak grafa tiče, tu ne mogu biti od velike pomoći - sve korisne informacije zapravo imaš gore. 
Evo, nisam bio baš detaljan, ali s takvim zadatkom... tko bi bio. 
|




