|
Možda je ovako lakše objasniti (mislim, to je ista stvar, samo drugim riječima :D): pretpostavi da je [latex]c[/latex] negativan. Sad, kako [latex](c_n)_n[/latex] konvergira u [latex]c[/latex], po definiciji vrijedi [latex](\forall \varepsilon >0)(\exists n_0\in\mathbb{N})(n\geq n_0, n\in\mathbb{N}\implies |c_n-c|<\varepsilon)[/latex]. E, sad uzmi [latex]\varepsilon=\displaystyle\frac{|c|}{2}[/latex] (to je dosta standardan trik kod ovakvog ispitivanja pozitivnosti, upravo iz razloga koji ćemo upravo izvesti).
Dakle, morao bi postojati neki [latex]n_0[/latex] takav da vrijedi ono gore za sve [latex]n\geq n_0[/latex]. Specifično (treba nam samo jedan član koji je u kontradikciji), i za sam [latex]n_0[/latex] mora vrijediti [latex]\displaystyle |c_{n_0}-c|<\frac{|c|}{2}[/latex]. No, to upravo znači da je [latex]c_{n_0}[/latex] iz intervala [latex]\displaystyle \langle c-\frac{|c|}{2}, c+\frac{|c|}{2}\rangle[/latex]. Eh, a [latex]c[/latex] je negativan, pa je ovaj interval gore zapravo [latex]\langle 3c/2, c/2\rangle[/latex]. No, taj cijeli interval čine samo negativni brojevi. Kako je [latex]c_{n_0}\geq 0[/latex], došli smo do kontradikcije.
Ah, fejky bje brži. :D (Inače, baš ovaj interval gore uzimamo zbog toga što smo lako pokazali da je on cijeli konstantnog predznaka (primijetit ćeš da je i za pozitivne [latex]c[/latex] opet cijeli [latex]\displaystyle \langle c-\frac{|c|}{2}, c+\frac{|c|}{2}\rangle[/latex] pozitivan). Mogli smo uzeti i [latex]|c|/3[/latex], [latex]7|c|/8[/latex] ili nešto četvrto, ali ovo je recimo najprirodnije. :) Mogli smo zapravo uzeti i cijeli [latex]|c|[/latex], to bi isto prošlo, ali se ovako "osjećamo sigurniji" - ne moramo razmišljati da nam je u redu i to kad je [latex]0[/latex] na rubu intervala, a interval je otvoren.)
Možda je ovako lakše objasniti (mislim, to je ista stvar, samo drugim riječima  ): pretpostavi da je ): pretpostavi da je  negativan. Sad, kako negativan. Sad, kako 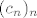 konvergira u konvergira u  , po definiciji vrijedi , po definiciji vrijedi 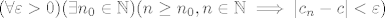 . E, sad uzmi . E, sad uzmi 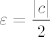 (to je dosta standardan trik kod ovakvog ispitivanja pozitivnosti, upravo iz razloga koji ćemo upravo izvesti). (to je dosta standardan trik kod ovakvog ispitivanja pozitivnosti, upravo iz razloga koji ćemo upravo izvesti).
Dakle, morao bi postojati neki 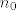 takav da vrijedi ono gore za sve takav da vrijedi ono gore za sve  . Specifično (treba nam samo jedan član koji je u kontradikciji), i za sam . Specifično (treba nam samo jedan član koji je u kontradikciji), i za sam 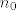 mora vrijediti mora vrijediti 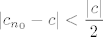 . No, to upravo znači da je . No, to upravo znači da je 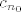 iz intervala iz intervala 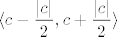 . Eh, a . Eh, a  je negativan, pa je ovaj interval gore zapravo je negativan, pa je ovaj interval gore zapravo 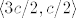 . No, taj cijeli interval čine samo negativni brojevi. Kako je . No, taj cijeli interval čine samo negativni brojevi. Kako je 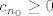 , došli smo do kontradikcije. , došli smo do kontradikcije.
Ah, fejky bje brži.  (Inače, baš ovaj interval gore uzimamo zbog toga što smo lako pokazali da je on cijeli konstantnog predznaka (primijetit ćeš da je i za pozitivne (Inače, baš ovaj interval gore uzimamo zbog toga što smo lako pokazali da je on cijeli konstantnog predznaka (primijetit ćeš da je i za pozitivne  opet cijeli opet cijeli 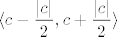 pozitivan). Mogli smo uzeti i pozitivan). Mogli smo uzeti i 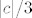 , , 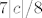 ili nešto četvrto, ali ovo je recimo najprirodnije. ili nešto četvrto, ali ovo je recimo najprirodnije.  Mogli smo zapravo uzeti i cijeli Mogli smo zapravo uzeti i cijeli 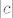 , to bi isto prošlo, ali se ovako "osjećamo sigurniji" - ne moramo razmišljati da nam je u redu i to kad je , to bi isto prošlo, ali se ovako "osjećamo sigurniji" - ne moramo razmišljati da nam je u redu i to kad je  na rubu intervala, a interval je otvoren.) na rubu intervala, a interval je otvoren.)
|






