| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 15:27 uto, 10. 5. 2011 Naslov: Postano: 15:27 uto, 10. 5. 2011 Naslov: |
    |
|
|
Da li je ideal maksimalan se rijetko kad provjerava pomoću definicije. Općenito se koristi karakterizacija da ako je R/M prsten s dijeljenjem, onda je M maksimalan ideal u R (ili slična tvrdnja u kojoj se kaže da za komutativan prsten R s jedinicom vrijedi da je R/M polje ako i samo ako je M maksimalan ideal).
Postoje karatkerizacije za posebne slučajeve, npr. u prstenu Z je svaki maksimalan ideal prost ideal, a lako se odredi koji su to prosti ideali.
U tvom zadatku se ništa od toga ne koristi već se samo želi provjeriti da li ste s razumijevanjem pročitali definiciju maksimalnog ideala.
Npr. u prvoj grupi, nakon što dokažeš da je I ideal, uočiš da je identiteta, odnosno f:<-1,1> -> R td. f(x)=x sadržana u I. S obzirom da je f očito bijekcija na restrikciji na <-1,1>, onda je i invertibilna na <-1,1> pa iz toga slijedi da I sadrži barem jedan invertibilan element. To znači da je I jednak cijelom C(<-1,1>), no u definiciji maksimalnog ideala stoji da maksimalan ideal [b]ne smije biti čitav prsten[/b] pa I neće biti maksimalan ideal.
Bolji primjer za f je [latex]f(x)=\tan{\frac{\pi}{2}x}[/latex] čija je domena <-1,1>, kodomena čitav R i koja je bijektivna pa i invertibilna na <-1,1>.
Da li je ideal maksimalan se rijetko kad provjerava pomoću definicije. Općenito se koristi karakterizacija da ako je R/M prsten s dijeljenjem, onda je M maksimalan ideal u R (ili slična tvrdnja u kojoj se kaže da za komutativan prsten R s jedinicom vrijedi da je R/M polje ako i samo ako je M maksimalan ideal).
Postoje karatkerizacije za posebne slučajeve, npr. u prstenu Z je svaki maksimalan ideal prost ideal, a lako se odredi koji su to prosti ideali.
U tvom zadatku se ništa od toga ne koristi već se samo želi provjeriti da li ste s razumijevanjem pročitali definiciju maksimalnog ideala.
Npr. u prvoj grupi, nakon što dokažeš da je I ideal, uočiš da je identiteta, odnosno f:←1,1> → R td. f(x)=x sadržana u I. S obzirom da je f očito bijekcija na restrikciji na ←1,1>, onda je i invertibilna na ←1,1> pa iz toga slijedi da I sadrži barem jedan invertibilan element. To znači da je I jednak cijelom C(←1,1>), no u definiciji maksimalnog ideala stoji da maksimalan ideal ne smije biti čitav prsten pa I neće biti maksimalan ideal.
Bolji primjer za f je 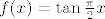 čija je domena ←1,1>, kodomena čitav R i koja je bijektivna pa i invertibilna na ←1,1>. čija je domena ←1,1>, kodomena čitav R i koja je bijektivna pa i invertibilna na ←1,1>.
_________________
The Dude Abides
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 21:43 uto, 10. 5. 2011 Naslov: Postano: 21:43 uto, 10. 5. 2011 Naslov: |
    |
|
|
[quote="pmli"]Zar nije da se u ovom zadatku radi o prstenu [latex](C(\langle -1, 1 \rangle), + , \cdot)[/latex], a ne [latex](C(\langle -1, 1 \rangle), + , \circ)[/latex] (čini mi se da čak I nije ideal u ovom drugom slučaju)?[/quote]
Imaš pravo, previdio sam da se radi o množenju po točkama, htio sam da bude jednostavan zadatak. :)
Ipak se treba upotrijebiti karakterizacija maksimalnog ideala: ne-nul elementi u R/I su elementi oblika f+I gdje f nije iz I, tj. [latex]f(0)\neq 0[/latex].
Neka f nije iz I. Definiramo g td. g(x)=f(0) za -1<x<1. Tada očito g nije u I, ali f-g je u I jer je (f-g)(0)=f(0)-g(0)=f(0)-f(0)=0.
Jer je f-g u I mora biti f+I=g+I, a jer g nije nikada nula, onda g ima inverz 1/g pa g+I ima inverz, odnosno f+I ima inverz u C/I i on je jednak 1/g+I. Kako iz toga slijedi da je u C/I svaki ne-nul element invertibilan, C/I je polje pa je I maksimalan ideal.
da vidimo što sam ovaj put previdio... :cry:
| pmli (napisa): | Zar nije da se u ovom zadatku radi o prstenu 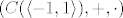 , a ne , a ne 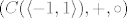 (čini mi se da čak I nije ideal u ovom drugom slučaju)? (čini mi se da čak I nije ideal u ovom drugom slučaju)? |
Imaš pravo, previdio sam da se radi o množenju po točkama, htio sam da bude jednostavan zadatak. 
Ipak se treba upotrijebiti karakterizacija maksimalnog ideala: ne-nul elementi u R/I su elementi oblika f+I gdje f nije iz I, tj. 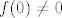 . .
Neka f nije iz I. Definiramo g td. g(x)=f(0) za -1<x<1. Tada očito g nije u I, ali f-g je u I jer je (f-g)(0)=f(0)-g(0)=f(0)-f(0)=0.
Jer je f-g u I mora biti f+I=g+I, a jer g nije nikada nula, onda g ima inverz 1/g pa g+I ima inverz, odnosno f+I ima inverz u C/I i on je jednak 1/g+I. Kako iz toga slijedi da je u C/I svaki ne-nul element invertibilan, C/I je polje pa je I maksimalan ideal.
da vidimo što sam ovaj put previdio... 
_________________
The Dude Abides
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 9:39 sri, 11. 5. 2011 Naslov: Postano: 9:39 sri, 11. 5. 2011 Naslov: |
    |
|
|
[quote="goranm"]g nije nikada nula[/quote]
Zašto? Može biti, npr. [latex]g(x) = 1 - 4 x^2[/latex]. ;)
EDIT: Sorry, moram se ispraviti! :oops: Nisam primjetio x u
[quote="goranm"]g(x)=f(0)[/quote]
Dakle, sve je super. :)
Ali da, bitno je uočiti da je svaka klasa oblika [latex]\{f \in C(\langle -1, 1 \rangle) : f(0) = c\}[/latex], gdje je [latex]c \in \mathbb{R}[/latex]. Lako se vidi kako se te klase zbrajaju i množe, pa kada je neka klasa invertibilna.
| goranm (napisa): | | g nije nikada nula |
Zašto? Može biti, npr. 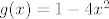 . . 
EDIT: Sorry, moram se ispraviti!  Nisam primjetio x u Nisam primjetio x u
| goranm (napisa): | | g(x)=f(0) |
Dakle, sve je super. 
Ali da, bitno je uočiti da je svaka klasa oblika 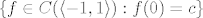 , gdje je , gdje je 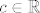 . Lako se vidi kako se te klase zbrajaju i množe, pa kada je neka klasa invertibilna. . Lako se vidi kako se te klase zbrajaju i množe, pa kada je neka klasa invertibilna.
Zadnja promjena: pmli; 11:42 sri, 11. 5. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
|













