|
[quote="kikzmyster"]Asistent Gogic je na vjezbama dao sljedecu napomenu:
"Pretpostavimo da je [latex]\displaystyle\ f:<a,b>\to R [/latex] derivabilna na [latex]<a,b>[/latex] osim eventualno u tocki [latex]c\in<a,b>[/latex]. Pretpostavimo da postoje limesi [latex]\displaystyle\lim_{x\to c^{-}}f'(x) [/latex] i [latex]\displaystyle\lim_{x\to c^{+}}f'(x) [/latex]
Tada su lijeva i desna derivacija jednake odgovarajucim limesima."
Sad, u napomeni se ne spominje neprekidnost funkcije [latex]f[/latex] u [latex]c[/latex], ali mi se cini da je to nuzan uvjet da bi vrijedilo sve ovo (dolazim do male kontradikcije u jednom zadatku ako nije, a i ne znam kako bi dokazao ovu napomenu bez te pretpostavke). Jeli mora onda f bit neprekidna u c?[/quote]
Dobro kažeš, treba zahtjevati i neprekidnost u [latex]c[/latex]. Kontraprimjer bi bila funkcija [latex]f(x)=0[/latex] na [latex]\langle 0,1][/latex] i [latex]f(x)=1[/latex] na [latex]\langle 1,2\rangle[/latex]
| kikzmyster (napisa): | Asistent Gogic je na vjezbama dao sljedecu napomenu:
"Pretpostavimo da je 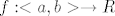 derivabilna na derivabilna na 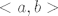 osim eventualno u tocki osim eventualno u tocki 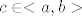 . Pretpostavimo da postoje limesi . Pretpostavimo da postoje limesi 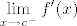 i i 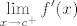
Tada su lijeva i desna derivacija jednake odgovarajucim limesima."
Sad, u napomeni se ne spominje neprekidnost funkcije  u u  , ali mi se cini da je to nuzan uvjet da bi vrijedilo sve ovo (dolazim do male kontradikcije u jednom zadatku ako nije, a i ne znam kako bi dokazao ovu napomenu bez te pretpostavke). Jeli mora onda f bit neprekidna u c? , ali mi se cini da je to nuzan uvjet da bi vrijedilo sve ovo (dolazim do male kontradikcije u jednom zadatku ako nije, a i ne znam kako bi dokazao ovu napomenu bez te pretpostavke). Jeli mora onda f bit neprekidna u c? |
Dobro kažeš, treba zahtjevati i neprekidnost u  . Kontraprimjer bi bila funkcija . Kontraprimjer bi bila funkcija 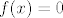 na na 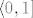 i i 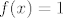 na na 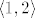
|






