| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
maaajčiii
Forumaš(ica)

Pridružen/a: 05. 01. 2011. (12:11:11)
Postovi: (2D)16
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
maaajčiii
Forumaš(ica)

Pridružen/a: 05. 01. 2011. (12:11:11)
Postovi: (2D)16
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 0:02 sub, 2. 4. 2011 Naslov: Postano: 0:02 sub, 2. 4. 2011 Naslov: |
    |
|
|
Hint: Izrazi y'. Fiksiraj k=k1 i neka su sada x=x1 i y=y1 realni brojevi takvi da je y'(x1,y1)=k1. Sada trebas pronaci neke x2,y2 razlicite od x1,y1 takve da je y'(x2,y2)=y'(x1,y1)=k1.
Hint: Izrazi y'. Fiksiraj k=k1 i neka su sada x=x1 i y=y1 realni brojevi takvi da je y'(x1,y1)=k1. Sada trebas pronaci neke x2,y2 razlicite od x1,y1 takve da je y'(x2,y2)=y'(x1,y1)=k1.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 12:22 sub, 2. 4. 2011 Naslov: Postano: 12:22 sub, 2. 4. 2011 Naslov: |
    |
|
|
I kako dalje, treba izraziti x1, x2, y1, y2 i to je to, ili se mogu naci konkretne vrrijednosti, raspisivajuci dobila sam:
y2x1(2-x2)=y1x2(2-x1) i ne znam sta bi sad s tim mogla dalje uradit... :S
I kako dalje, treba izraziti x1, x2, y1, y2 i to je to, ili se mogu naci konkretne vrrijednosti, raspisivajuci dobila sam:
y2x1(2-x2)=y1x2(2-x1) i ne znam sta bi sad s tim mogla dalje uradit... :S
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 14:32 sub, 2. 4. 2011 Naslov: Postano: 14:32 sub, 2. 4. 2011 Naslov: |
    |
|
|
Imam jos jedno pitanje, na tom istom kolokviju, treci zadatak:
tamo gdje treba odrediti glob min i max na [-1,3],
znamo da pod kriticne tocke spadaju: 1) rubne toce intervala, 2) nultocke, e sad ona treca grupa me malo buni, u nasem slucaju, da li su kriticne tocke sve one između -1 i 3, ili samo 0, jer je funk derivabilna na <-besk, 0> i <0, +besk> pa onda eventualno nije derivabilna u 0.
To me buni jer smo na vjezbama uradili jedan zadatak, tj.
f(x)=3korjen (x) * 3korjen [(1+x)^2 ] i rekli smo da je derivabilna na <-1,0>, <0,1>, <-1,2>, i rekli da eventualno nije derivab u 0 i 1. (zato pitam za tocke između -1 i 3)
Također ako je netko rijesio taj zadatak: da li je rjesenje BETA= PI/4, ALFA=1/2?
Hvala unaprijed. :)
Imam jos jedno pitanje, na tom istom kolokviju, treci zadatak:
tamo gdje treba odrediti glob min i max na [-1,3],
znamo da pod kriticne tocke spadaju: 1) rubne toce intervala, 2) nultocke, e sad ona treca grupa me malo buni, u nasem slucaju, da li su kriticne tocke sve one između -1 i 3, ili samo 0, jer je funk derivabilna na ←besk, 0> i <0, +besk> pa onda eventualno nije derivabilna u 0.
To me buni jer smo na vjezbama uradili jedan zadatak, tj.
f(x)=3korjen (x) * 3korjen [(1+x)^2 ] i rekli smo da je derivabilna na ←1,0>, <0,1>, ←1,2>, i rekli da eventualno nije derivab u 0 i 1. (zato pitam za tocke između -1 i 3)
Također ako je netko rijesio taj zadatak: da li je rjesenje BETA= PI/4, ALFA=1/2?
Hvala unaprijed. 
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
 Postano: 15:42 sub, 2. 4. 2011 Naslov: Postano: 15:42 sub, 2. 4. 2011 Naslov: |
    |
|
|
Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i f'(0) nije nula pa 0 ne može biti ekstrem. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima).
Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i f'(0) nije nula pa 0 ne može biti ekstrem. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima).
_________________
nekad sam bio umišljen al sam se promijenio sad sam savršen
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 16:56 sub, 2. 4. 2011 Naslov: Postano: 16:56 sub, 2. 4. 2011 Naslov: |
    |
|
|
[quote="zvonkec"]
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
[/quote]
To je tocno :).
[quote="zvonkec"]Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?[/quote]
Primjeti: [latex]x=1-2k[/latex], [latex]y=2-k[/latex] :)
| zvonkec (napisa): |
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
|
To je tocno  . .
| zvonkec (napisa): | | Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"? |
Primjeti: 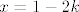 , , 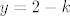 
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 17:46 sub, 2. 4. 2011 Naslov: Postano: 17:46 sub, 2. 4. 2011 Naslov: |
    |
|
|
Nema frke, stvar je u tome samo da [latex]\frac{2x-y}{x-2y}=k[/latex] izmnozis i dobijes: [latex]x(2-k)=y(1-2k)[/latex] i sada samo izjednacis strane tako da stavis [latex]x=1-2k[/latex] i [latex]y=2-k[/latex]. Onda su ocito lijeva i desna strana jednake, te je taj izbor x,y jedno rješenje jednadžbe..time si i pokazao da za fiksan k postoje x,y takve da je y'(x,y)=k (jer si nasao primjer). :)
Nema frke, stvar je u tome samo da 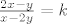 izmnozis i dobijes: izmnozis i dobijes: 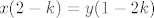 i sada samo izjednacis strane tako da stavis i sada samo izjednacis strane tako da stavis 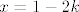 i i 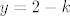 . Onda su ocito lijeva i desna strana jednake, te je taj izbor x,y jedno rješenje jednadžbe..time si i pokazao da za fiksan k postoje x,y takve da je y'(x,y)=k (jer si nasao primjer). . Onda su ocito lijeva i desna strana jednake, te je taj izbor x,y jedno rješenje jednadžbe..time si i pokazao da za fiksan k postoje x,y takve da je y'(x,y)=k (jer si nasao primjer). 
|
|
| [Vrh] |
|
mata
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (17:50:57)
Postovi: (17)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
mata
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (17:50:57)
Postovi: (17)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 18:35 sub, 2. 4. 2011 Naslov: Postano: 18:35 sub, 2. 4. 2011 Naslov: |
    |
|
|
[quote="zvonkec"]Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i [b]f'(0) nije nula pa 0 ne može biti ekstrem[/b]. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima).[/quote]
Hmm, sve razumijem, ali ovo podebljano bas i ne, ako te dobro razumijem, derivacija u bilo kojoj kriticnoj tocki bi trebala iznositi 0, da bi uopce mogli reci da je globalni min/max, a u ovom slucaju nasem ne znam bas kako bi to proslo...
ja dobila glob max = (114 + PI)/4, a buduci si rekao da je svejedno uzmemo li sve tocke kao "kriticne tocke" mislim da ovdje opet nije svjedeno, jer ako uzmemo da je 0 kriticna tocka onda glob min iznosi PI/4 (upravo taj f(0) ), a inace bi bio bez te 0, f(-1)= (10 + PI)/4.
Hvala na onom prvom pojasnjenom pitanju.
Jos me zanima: kako je lim (x-->1) [ ln(2x) - ln2 ] / [x-1]= 1 ??? :oops:
| zvonkec (napisa): | Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i f'(0) nije nula pa 0 ne može biti ekstrem. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima). |
Hmm, sve razumijem, ali ovo podebljano bas i ne, ako te dobro razumijem, derivacija u bilo kojoj kriticnoj tocki bi trebala iznositi 0, da bi uopce mogli reci da je globalni min/max, a u ovom slucaju nasem ne znam bas kako bi to proslo...
ja dobila glob max = (114 + PI)/4, a buduci si rekao da je svejedno uzmemo li sve tocke kao "kriticne tocke" mislim da ovdje opet nije svjedeno, jer ako uzmemo da je 0 kriticna tocka onda glob min iznosi PI/4 (upravo taj f(0) ), a inace bi bio bez te 0, f(-1)= (10 + PI)/4.
Hvala na onom prvom pojasnjenom pitanju.
Jos me zanima: kako je lim (x→1) [ ln(2x) - ln2 ] / [x-1]= 1 ??? 
|
|
| [Vrh] |
|
mata
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (17:50:57)
Postovi: (17)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
|















