| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 17:33 pet, 27. 6. 2008 Naslov: Postano: 17:33 pet, 27. 6. 2008 Naslov: |
    |
|
|
Nešto radiš (ili radite, ne znam s koliko gostiju razgovaram) krivo...
[latex]\displaystyle
\sum_{i\in\omega\cdot 3}(i^3+3^i) = \sum_{i\in\omega}(i^3+3^i) +
\sum_{i\in\omega}\big((\omega+i)^3+3^{\omega+i}\big) +
\sum_{i\in\omega}\big((\omega\cdot 2+ i)^3+3^{\omega\cdot 2+i}\big)[/latex]
Raspišimo redom svaku sumu:
[latex]
\begin{aligned}
\sum_{i\in\omega}(i^3+3^i) & = \sup_{n\in\omega}\sum_{i\in n}(i^3+3^i) \\
& = \sup_{n\in\omega} a_n \\
& = \omega
\end{aligned}
[/latex]
pri čemu je [latex](a_n)_{n\in\omega}[/latex] strogo rastući niz konačnih ordinala.
Nadalje,
[latex]
\begin{aligned}
\sum_{i\in\omega}\big((\omega+i)^3+3^{\omega+i}\big)
& = \sum_{i\in\omega}\big(\omega^3+\omega^2\cdot i + \omega\cdot i + i + \omega\cdot 3^i\big) \\
& = \sup_{n\in\omega}\sum_{i\in n}\big(\omega^3+\omega^2\cdot i + \omega\cdot (i + 3^i)\big) \\
& = \sup_{n\in\omega}\big(\omega^3\cdot n + \omega^2\cdot (n-1)+\omega\cdot (n-1+3^{n-1})\big) \\
& = \omega^4
\end{aligned}
[/latex]
Pritom smo, između ostalog, koristili [latex](\omega+i)^3=\omega^3+\omega^2\cdot i + \omega\cdot i + i[/latex] i [latex]3^\omega=\omega[/latex]. Možda je potrebno objasniti zadnji korak:
Vrijedi [latex]\omega^3\cdot n + \omega^2\cdot (n-1)+\omega\cdot (n-1+3^{n-1})<\omega^4[/latex] za svaki [latex]n\in\omega[/latex].
Nadalje, svaki ordinal manji od [latex]\omega^4[/latex] je oblika [latex]\omega^3\cdot j+\omega^2\cdot k+\omega\cdot l+m[/latex] za neke [latex]j,k,l,m\in\omega[/latex] pa za [latex]n=j+1[/latex] imamo [latex]\omega^3\cdot n + \omega^2\cdot (n-1)+\omega\cdot (n-1+3^{n-1})>\omega^3\cdot j+\omega^2\cdot k+\omega\cdot l+m[/latex].
Stoga je
[latex]\displaystyle
\sup_{n\in\omega}\big(\omega^3\cdot n + \omega^2\cdot (n-1)+\omega\cdot (n-1+3^{n-1})\big) = \omega^4[/latex]
Slično se dobije i da je zadnja suma [latex]\omega^4[/latex]. Sve skupa:
[latex]\displaystyle
\sum_{i\in\omega\cdot 3}(i^3+3^i) =\omega+\omega^4+\omega^4=\omega^4\cdot 2[/latex]
Nešto radiš (ili radite, ne znam s koliko gostiju razgovaram) krivo...
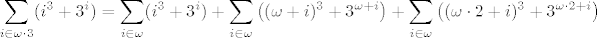
Raspišimo redom svaku sumu:
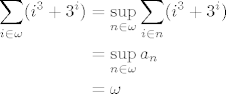
pri čemu je 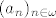 strogo rastući niz konačnih ordinala. strogo rastući niz konačnih ordinala.
Nadalje,
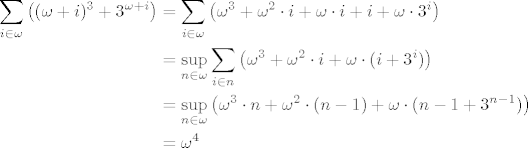
Pritom smo, između ostalog, koristili 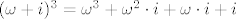 i i 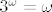 . Možda je potrebno objasniti zadnji korak: . Možda je potrebno objasniti zadnji korak:
Vrijedi 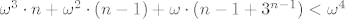 za svaki za svaki 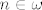 . .
Nadalje, svaki ordinal manji od 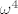 je oblika je oblika 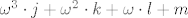 za neke za neke 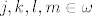 pa za pa za 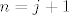 imamo imamo 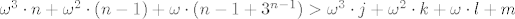 . .
Stoga je
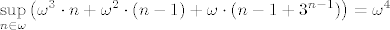
Slično se dobije i da je zadnja suma 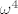 . Sve skupa: . Sve skupa:
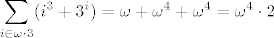
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
majaa
Gost
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Void
Forumaš(ica)

Pridružen/a: 14. 11. 2002. (18:08:22)
Postovi: (FA)16
|
 Postano: 9:50 ned, 29. 6. 2008 Naslov: Postano: 9:50 ned, 29. 6. 2008 Naslov: |
    |
|
|
[quote="majaa"]Moze uputa za zad 158 iz zbirke, kako dokazati da ta dva skupa nisu slicni?[/quote]
Prvo što u tom zadatku treba primjetiti je da se dokazuje da neki skup nije sličan s [latex]\mathbb{R}[/latex]. Kad bi za taj skup vrijedili svi uvjeti iz teorema o uređajnoj karakteristici skupa [latex]\mathbb{R}[/latex], onda bi po tom teoremu morao biti sličan s [latex]\mathbb{R}[/latex]. Dakle, ako nije sličan, onda sigurno ne vrijedi jedan od uvjeta iz teorema o uređajnoj karakteristici. Sad ostaje pitanje koji uvjet ne vrijedi. Inače, ti su uvjeti invarijante sličnosti pa ako pokažemo da skup [latex]\mathbb{R} \times \mathbb{R}[/latex] nema jednu od tih invarijanti, onda odmah zaključujemo da nije sličan s [latex]\mathbb{R}[/latex].
Ako malo razmislimo o tome kako uređaj iz zadatka izgleda, nije teško doći do toga da skup [latex]\mathbb{R} \times \left<0, 1\right>[/latex] nema supremum iako je odozgo omeđen. Omeđenost je trivijalna jer je jedna gornja međa element [latex](0, 1)[/latex]. Ostaje još samo vidjeti da taj skup nema supremum u [latex]\mathbb{R} \times \mathbb{R}[/latex], tj. da nema najmanju gornju među. Svaka gornja međa skupa [latex]\mathbb{R} \times \left<0, 1\right>[/latex] je oblika [latex](a, b)[/latex], gdje su [latex]a \in \mathbb{R}, b \ge 1[/latex]. Najmanja gornja međa bi očito morala na drugoj koordinati imati [latex]b = 1[/latex]. A što je sa prvom koordinatom? Ako uzmemo neki [latex]a \in \mathbb{R}[/latex] proizvoljan, onda je gornja međa [latex](a - 1, b)[/latex] manja od gornje međe [latex](a, b)[/latex]. Dakle, ne postoji najmanja gornja međa skupa [latex]\mathbb{R} \times \left<0, 1\right>[/latex].
| majaa (napisa): | | Moze uputa za zad 158 iz zbirke, kako dokazati da ta dva skupa nisu slicni? |
Prvo što u tom zadatku treba primjetiti je da se dokazuje da neki skup nije sličan s  . Kad bi za taj skup vrijedili svi uvjeti iz teorema o uređajnoj karakteristici skupa . Kad bi za taj skup vrijedili svi uvjeti iz teorema o uređajnoj karakteristici skupa  , onda bi po tom teoremu morao biti sličan s , onda bi po tom teoremu morao biti sličan s  . Dakle, ako nije sličan, onda sigurno ne vrijedi jedan od uvjeta iz teorema o uređajnoj karakteristici. Sad ostaje pitanje koji uvjet ne vrijedi. Inače, ti su uvjeti invarijante sličnosti pa ako pokažemo da skup . Dakle, ako nije sličan, onda sigurno ne vrijedi jedan od uvjeta iz teorema o uređajnoj karakteristici. Sad ostaje pitanje koji uvjet ne vrijedi. Inače, ti su uvjeti invarijante sličnosti pa ako pokažemo da skup 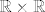 nema jednu od tih invarijanti, onda odmah zaključujemo da nije sličan s nema jednu od tih invarijanti, onda odmah zaključujemo da nije sličan s  . .
Ako malo razmislimo o tome kako uređaj iz zadatka izgleda, nije teško doći do toga da skup 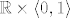 nema supremum iako je odozgo omeđen. Omeđenost je trivijalna jer je jedna gornja međa element nema supremum iako je odozgo omeđen. Omeđenost je trivijalna jer je jedna gornja međa element 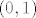 . Ostaje još samo vidjeti da taj skup nema supremum u . Ostaje još samo vidjeti da taj skup nema supremum u 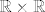 , tj. da nema najmanju gornju među. Svaka gornja međa skupa , tj. da nema najmanju gornju među. Svaka gornja međa skupa 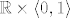 je oblika je oblika 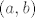 , gdje su , gdje su 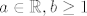 . Najmanja gornja međa bi očito morala na drugoj koordinati imati . Najmanja gornja međa bi očito morala na drugoj koordinati imati 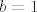 . A što je sa prvom koordinatom? Ako uzmemo neki . A što je sa prvom koordinatom? Ako uzmemo neki 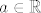 proizvoljan, onda je gornja međa proizvoljan, onda je gornja međa 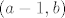 manja od gornje međe manja od gornje međe 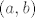 . Dakle, ne postoji najmanja gornja međa skupa . Dakle, ne postoji najmanja gornja međa skupa 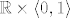 . .
|
|
| [Vrh] |
|
lena
Forumaš(ica)


Pridružen/a: 09. 12. 2005. (21:21:59)
Postovi: (4C)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
DoTo
Forumaš(ica)

Pridružen/a: 08. 07. 2007. (13:42:28)
Postovi: (8)16
|
|
| [Vrh] |
|
majaa
Gost
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 15:24 ned, 29. 6. 2008 Naslov: Postano: 15:24 ned, 29. 6. 2008 Naslov: |
    |
|
|
[quote="DoTo"]@melkior: I ja dobivam kao i ti. To je jedini zadatak od onih koje sam rijesio iz zbirke a da nisam dobio prema rjesenjima, ali opet mislim da rjesenje u zbirci nije dobro. Pa ako ima neko da me (nas) razuvjeri....[/quote]
Dokaz ti nije dovoljno uvjerljiv? :) Već smo ustanovili da ni za 193. b nije točno rješenje u zbirci.
Btw, krivo si mi napisao ime...
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
[quote="majaa"]Jel vama 193. pod c i pod i ispada kao u rjesenjima, jer meni nije a sve mi se cini ok :roll:[/quote]
Da, čini se da su zamijenili rješenja od 193. b i c. Nemojte se čuditi ako naiđete na ovakve greške. Zbirka je u fazi nastajanja i normalno je da se potkradaju tipfeleri i greške.
Inače, bilo bi lijepo da kad pitate za neki zadatak napišete kako ste rješavali i što ste dobili. Na taj način je puno lakše uočiti što eventualno radite krivo.
| DoTo (napisa): | | @melkior: I ja dobivam kao i ti. To je jedini zadatak od onih koje sam rijesio iz zbirke a da nisam dobio prema rjesenjima, ali opet mislim da rjesenje u zbirci nije dobro. Pa ako ima neko da me (nas) razuvjeri.... |
Dokaz ti nije dovoljno uvjerljiv?  Već smo ustanovili da ni za 193. b nije točno rješenje u zbirci. Već smo ustanovili da ni za 193. b nije točno rješenje u zbirci.
Btw, krivo si mi napisao ime...
Added after 11 minutes:
| majaa (napisa): | Jel vama 193. pod c i pod i ispada kao u rjesenjima, jer meni nije a sve mi se cini ok  |
Da, čini se da su zamijenili rješenja od 193. b i c. Nemojte se čuditi ako naiđete na ovakve greške. Zbirka je u fazi nastajanja i normalno je da se potkradaju tipfeleri i greške.
Inače, bilo bi lijepo da kad pitate za neki zadatak napišete kako ste rješavali i što ste dobili. Na taj način je puno lakše uočiti što eventualno radite krivo.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
FFF
Forumaš(ica)


Pridružen/a: 19. 11. 2006. (19:46:12)
Postovi: (2A)16
|
|
| [Vrh] |
|
lena
Forumaš(ica)


Pridružen/a: 09. 12. 2005. (21:21:59)
Postovi: (4C)16
Spol: 
|
|
| [Vrh] |
|
Blah
Forumaš(ica)

Pridružen/a: 11. 09. 2006. (18:07:56)
Postovi: (C1)16
Spol: 
|
|
| [Vrh] |
|
FFF
Forumaš(ica)


Pridružen/a: 19. 11. 2006. (19:46:12)
Postovi: (2A)16
|
|
| [Vrh] |
|
saki
Forumaš(ica)

Pridružen/a: 03. 02. 2008. (14:02:23)
Postovi: (1D)16
|
|
| [Vrh] |
|
|













