|
Naprosto se radi o oduzimanju prethodna dva reda. Možda će biti jasnije ako se to malo raspiše.
Dakle, imaš [latex]\displaystyle\ln(1-n)=\sum_{n=1}^{+\infty}b_nx^n[/latex], pri čemu je [latex]\displaystyle b_n=-\frac{1}{n}[/latex] za svaki [latex]n\in\mathbb{N}[/latex].
Također, imaš [latex]\displaystyle\ln(1-n^3)=\sum_{n=1}^{+\infty}c_nx^n[/latex], pri čemu su [latex]c_n[/latex] zadani ovako: ako [latex]3\mid n[/latex], onda je [latex]\displaystyle c_n=-\frac{1}{n/3}[/latex] (jer se uz članove oblika [latex]x^{3k}[/latex] pojavljuje koeficijent oblika [latex]\displaystyle -\frac{1}{k})[/latex]. Ostali članovi "ne postoje", tj. [latex]c_n=0[/latex] ako [latex]3\nmid n[/latex].
Sad, [latex]a_n=c_n-b_n[/latex], što znači da, ako [latex]3\mid n[/latex], [latex]\displaystyle a_n=-\frac{1}{n/3}+\frac{1}{n}=-\frac{2}{n}[/latex], a ako [latex]3\nmid n[/latex], [latex]\displaystyle a_n=0+\frac{1}{n}=\frac{1}{n}[/latex].
In a state of peaceful happiness? :)
Naprosto se radi o oduzimanju prethodna dva reda. Možda će biti jasnije ako se to malo raspiše.
Dakle, imaš 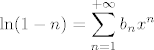 , pri čemu je , pri čemu je 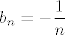 za svaki za svaki 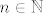 . .
Također, imaš 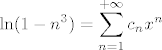 , pri čemu su , pri čemu su 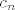 zadani ovako: ako zadani ovako: ako 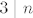 , onda je , onda je  (jer se uz članove oblika (jer se uz članove oblika  pojavljuje koeficijent oblika pojavljuje koeficijent oblika  . Ostali članovi "ne postoje", tj. . Ostali članovi "ne postoje", tj. 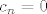 ako ako 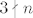 . .
Sad, 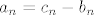 , što znači da, ako , što znači da, ako 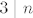 , , 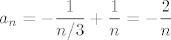 , a ako , a ako 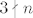 , , 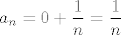 . .
In a state of peaceful happiness? 
|




