| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 10:20 ned, 5. 6. 2011 Naslov: Primjene određenih integrala Postano: 10:20 ned, 5. 6. 2011 Naslov: Primjene određenih integrala |
    |
|
|
U slucaju da ne budemo znali sebi nacrtati skicu, postoji li mogucnost da ikako dođemo do rezultata, ili djelomicno da uspijemo rjesit taj zadatak, bar za nekoliko bodova?
Brinu me one polarne koordinate... :S :s :s
I ako se moze, moze li netko dati upute kako rijesiti proslogodisnji 2.zad?
U slucaju da ne budemo znali sebi nacrtati skicu, postoji li mogucnost da ikako dođemo do rezultata, ili djelomicno da uspijemo rjesit taj zadatak, bar za nekoliko bodova?
Brinu me one polarne koordinate... :S :s :s
I ako se moze, moze li netko dati upute kako rijesiti proslogodisnji 2.zad?
Zadnja promjena: frutabella; 10:22 ned, 5. 6. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 11:08 ned, 5. 6. 2011 Naslov: Postano: 11:08 ned, 5. 6. 2011 Naslov: |
    |
|
|
Pa, uglavnom se ne može bez crtanja krivulja... možda ako imaš dosta iskustva, i onda možeš neke stvari napamet u glavi zamislit - a da dođeš do tamo ti je trebalo crtanje krivulja. :D
[latex]r = 1 + cos(3\phi)[/latex] je ta krivulja iz prošlogodišnjeg zadatka i otprilike izgleda kao cvijet sa tri latice xD
( http://www.wolframalpha.com/input/?i=r+%3D+1+%2B+cos%283phi%29 )
Ima jedno zgodno svojstvo kosinusa koje nam pomaže tu cos(-x) = cos x, znači, dovoljno je samo nacrtati dio iznad x osi, pa ga preslikati ispod x osi - krivulja je simetrična u odnosu na x os.
(Isto tako, krivulje u kojima samo sinus igra ulogu su simetrične u odnosu na y os).
A kako nacrtati tu polovicu krivulje? Pa ono, nema neke prevelike mudrolije, uzmeš si nekoliko zgodnih kuteva i vidiš što ispada, gdje je maksimum...
Ne znam zbilja što bih tu dodatno rekao.
A sad kad si vidila sliku tog cvjetića :D, mislim da ti pada na pamet kako je ovdje najlakše izračunati površinu.
P.S. Ako hoćeš, mogu malo detaljnije napisati kako bih ja nacrtao ovu krivulju... ako će ti to pomoći. :/
Pa, uglavnom se ne može bez crtanja krivulja... možda ako imaš dosta iskustva, i onda možeš neke stvari napamet u glavi zamislit - a da dođeš do tamo ti je trebalo crtanje krivulja. 
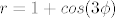 je ta krivulja iz prošlogodišnjeg zadatka i otprilike izgleda kao cvijet sa tri latice xD je ta krivulja iz prošlogodišnjeg zadatka i otprilike izgleda kao cvijet sa tri latice xD
( http://www.wolframalpha.com/input/?i=r+%3D+1+%2B+cos%283phi%29 )
Ima jedno zgodno svojstvo kosinusa koje nam pomaže tu cos(-x) = cos x, znači, dovoljno je samo nacrtati dio iznad x osi, pa ga preslikati ispod x osi - krivulja je simetrična u odnosu na x os.
(Isto tako, krivulje u kojima samo sinus igra ulogu su simetrične u odnosu na y os).
A kako nacrtati tu polovicu krivulje? Pa ono, nema neke prevelike mudrolije, uzmeš si nekoliko zgodnih kuteva i vidiš što ispada, gdje je maksimum...
Ne znam zbilja što bih tu dodatno rekao.
A sad kad si vidila sliku tog cvjetića  , mislim da ti pada na pamet kako je ovdje najlakše izračunati površinu. , mislim da ti pada na pamet kako je ovdje najlakše izračunati površinu.
P.S. Ako hoćeš, mogu malo detaljnije napisati kako bih ja nacrtao ovu krivulju... ako će ti to pomoći. 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 11:47 ned, 5. 6. 2011 Naslov: Postano: 11:47 ned, 5. 6. 2011 Naslov: |
    |
|
|
[quote="ceps"]Pa, uglavnom se ne može bez crtanja krivulja... možda ako imaš dosta iskustva, i onda možeš neke stvari napamet u glavi zamislit - a da dođeš do tamo ti je trebalo crtanje krivulja. :D
[latex]r = 1 + cos(3\phi)[/latex] je ta krivulja iz prošlogodišnjeg zadatka i otprilike izgleda kao cvijet sa tri latice xD
( http://www.wolframalpha.com/input/?i=r+%3D+1+%2B+cos%283phi%29 )
Ima jedno zgodno svojstvo kosinusa koje nam pomaže tu cos(-x) = cos x, znači, dovoljno je samo nacrtati dio iznad x osi, pa ga preslikati ispod x osi - krivulja je simetrična u odnosu na x os.
(Isto tako, krivulje u kojima samo sinus igra ulogu su simetrične u odnosu na y os).
A kako nacrtati tu polovicu krivulje? Pa ono, nema neke prevelike mudrolije, uzmeš si nekoliko zgodnih kuteva i vidiš što ispada, gdje je maksimum...
Ne znam zbilja što bih tu dodatno rekao.
A sad kad si vidila sliku tog cvjetića :D, mislim da ti pada na pamet kako je ovdje najlakše izračunati površinu.
P.S. Ako hoćeš, mogu malo detaljnije napisati kako bih ja nacrtao ovu krivulju... ako će ti to pomoći. :/[/quote]
Ako ti nije tesko, lijepo bih te zamolila, uz racun za povrsinu da imam neki koncept rjesavanja, mislim... stvarno mi je ovo bas ne ide.
| ceps (napisa): | Pa, uglavnom se ne može bez crtanja krivulja... možda ako imaš dosta iskustva, i onda možeš neke stvari napamet u glavi zamislit - a da dođeš do tamo ti je trebalo crtanje krivulja. 
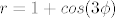 je ta krivulja iz prošlogodišnjeg zadatka i otprilike izgleda kao cvijet sa tri latice xD je ta krivulja iz prošlogodišnjeg zadatka i otprilike izgleda kao cvijet sa tri latice xD
( http://www.wolframalpha.com/input/?i=r+%3D+1+%2B+cos%283phi%29 )
Ima jedno zgodno svojstvo kosinusa koje nam pomaže tu cos(-x) = cos x, znači, dovoljno je samo nacrtati dio iznad x osi, pa ga preslikati ispod x osi - krivulja je simetrična u odnosu na x os.
(Isto tako, krivulje u kojima samo sinus igra ulogu su simetrične u odnosu na y os).
A kako nacrtati tu polovicu krivulje? Pa ono, nema neke prevelike mudrolije, uzmeš si nekoliko zgodnih kuteva i vidiš što ispada, gdje je maksimum...
Ne znam zbilja što bih tu dodatno rekao.
A sad kad si vidila sliku tog cvjetića  , mislim da ti pada na pamet kako je ovdje najlakše izračunati površinu. , mislim da ti pada na pamet kako je ovdje najlakše izračunati površinu.
P.S. Ako hoćeš, mogu malo detaljnije napisati kako bih ja nacrtao ovu krivulju... ako će ti to pomoći.  |
Ako ti nije tesko, lijepo bih te zamolila, uz racun za povrsinu da imam neki koncept rjesavanja, mislim... stvarno mi je ovo bas ne ide.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 12:37 ned, 5. 6. 2011 Naslov: Postano: 12:37 ned, 5. 6. 2011 Naslov: |
    |
|
|
A meni je ovo isto na početku predstavljalo bauk, pa sam se nakon nešto vremena i rješenih zadataka počeo snalaziti u svemu tome.
Znači, [latex]r = f(\phi)[/latex], udaljenost od ishodišta je funkcija kuta. Tako treba sve promatrat u tom okviru, maksimum je onda po tome najveća udaljenost od ishodišta itd.
Znači, [latex]r = 1 + cos(3\phi)[/latex], kao što sam već prije napomenuo, krivulja će biti simetrična u odnosu na x os, pa ću promatrati samo [latex]\phi \in [0, \pi][/latex].
Sada ću promatrati par kuteva za koje je jednostavno izračunati r, i usput se služiti onime što znam o trigonometrijskim funkcijama (dobro je cijelo vrijeme imati jediničnu kružnicu u glavi, možda je i nacrtat negdje sa strane :D ).
Ajmo prvo vidit za kuteve od 0 do [latex]\pi/3[/latex]... za kut 0, r = 2, a za kut [latex]\pi/3[/latex] r je 0.
Možeš si i uzet neku između vrijednost ako ti je tako lakše, ali znamo kako se kosinus ponaša na ovom intervalu, što je kut veći - kosinus je manji.
U pi/6 (točno na ''pola puta'' između 0 i [latex]\pi/3[/latex]) je kosinus trostrukog kuta 0, i zato tu [b]r[/b] iznosi 1 - nakon toga kosinus ide u minus sve dok ne dođe do - 1 u pi/3 -> i tada je vrijednost funkcije 0.
Ako pogledaš graf, vidit ćeš da se tako nešto i događa, ova krivulja koja s gornje strane spaja dvojku na x-osi i ishodište.
E sad, za [latex]\phi \in [\pi/3, \pi][/latex], je maksimum u [latex]2\pi/3[/latex] i opet iznosi 2... i nakon toga opet ''pada'' u ishodište, jer, kad je kut [latex]\pi[/latex] onda je [latex]1 + cos(3\pi) = 1 - 1 = 0[/latex]
Ovaj dio nije teško zamisliti na brojevnoj kružnici, nakon što je kut došao u [latex]2\pi[/latex] (zapamti, gleda se trostruki kut!), kosinus opet pada, isto kao što je opisano u prvom dijelu... (prelazi u minus itd.)...
A za računanje površine bih gledao samo ovaj dio od [latex]\phi \in [0, \pi/3][/latex] i kasnije ga pomnožio sa 6, mislim da je jasno zašto.
Ne znam, da li shvaćaš iz ovoga... teško je prenest nekom način razmišljanja.
Al eto, npr [latex]r = 1 + cos(5\phi)[/latex] je cvjetić sa 5 latica, [latex]r = 1 + sin(3\phi)[/latex] je također cvjetić sa 3 latice, samo simetričan u odnosu na y-os...
Argumentacija je slična kao u ovom slučaju... reci ako ima nejasnoća. :D
A meni je ovo isto na početku predstavljalo bauk, pa sam se nakon nešto vremena i rješenih zadataka počeo snalaziti u svemu tome.
Znači, 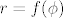 , udaljenost od ishodišta je funkcija kuta. Tako treba sve promatrat u tom okviru, maksimum je onda po tome najveća udaljenost od ishodišta itd. , udaljenost od ishodišta je funkcija kuta. Tako treba sve promatrat u tom okviru, maksimum je onda po tome najveća udaljenost od ishodišta itd.
Znači, 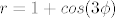 , kao što sam već prije napomenuo, krivulja će biti simetrična u odnosu na x os, pa ću promatrati samo , kao što sam već prije napomenuo, krivulja će biti simetrična u odnosu na x os, pa ću promatrati samo 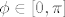 . .
Sada ću promatrati par kuteva za koje je jednostavno izračunati r, i usput se služiti onime što znam o trigonometrijskim funkcijama (dobro je cijelo vrijeme imati jediničnu kružnicu u glavi, možda je i nacrtat negdje sa strane  ). ).
Ajmo prvo vidit za kuteve od 0 do 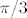 ... za kut 0, r = 2, a za kut ... za kut 0, r = 2, a za kut 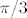 r je 0. r je 0.
Možeš si i uzet neku između vrijednost ako ti je tako lakše, ali znamo kako se kosinus ponaša na ovom intervalu, što je kut veći - kosinus je manji.
U pi/6 (točno na ''pola puta'' između 0 i 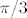 ) je kosinus trostrukog kuta 0, i zato tu r iznosi 1 - nakon toga kosinus ide u minus sve dok ne dođe do - 1 u pi/3 → i tada je vrijednost funkcije 0. ) je kosinus trostrukog kuta 0, i zato tu r iznosi 1 - nakon toga kosinus ide u minus sve dok ne dođe do - 1 u pi/3 → i tada je vrijednost funkcije 0.
Ako pogledaš graf, vidit ćeš da se tako nešto i događa, ova krivulja koja s gornje strane spaja dvojku na x-osi i ishodište.
E sad, za 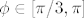 , je maksimum u , je maksimum u 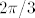 i opet iznosi 2... i nakon toga opet ''pada'' u ishodište, jer, kad je kut i opet iznosi 2... i nakon toga opet ''pada'' u ishodište, jer, kad je kut  onda je onda je 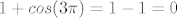
Ovaj dio nije teško zamisliti na brojevnoj kružnici, nakon što je kut došao u 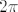 (zapamti, gleda se trostruki kut!), kosinus opet pada, isto kao što je opisano u prvom dijelu... (prelazi u minus itd.)... (zapamti, gleda se trostruki kut!), kosinus opet pada, isto kao što je opisano u prvom dijelu... (prelazi u minus itd.)...
A za računanje površine bih gledao samo ovaj dio od 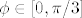 i kasnije ga pomnožio sa 6, mislim da je jasno zašto. i kasnije ga pomnožio sa 6, mislim da je jasno zašto.
Ne znam, da li shvaćaš iz ovoga... teško je prenest nekom način razmišljanja.
Al eto, npr 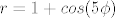 je cvjetić sa 5 latica, je cvjetić sa 5 latica, 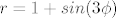 je također cvjetić sa 3 latice, samo simetričan u odnosu na y-os... je također cvjetić sa 3 latice, samo simetričan u odnosu na y-os...
Argumentacija je slična kao u ovom slučaju... reci ako ima nejasnoća. 
|
|
| [Vrh] |
|
fejky
Forumaš(ica)
Pridružen/a: 23. 06. 2010. (16:53:45)
Postovi: (3D)16
Spol: 
|
 Postano: 13:44 ned, 5. 6. 2011 Naslov: Postano: 13:44 ned, 5. 6. 2011 Naslov: |
    |
|
|
Mozda ovo nekome pomogne :D
Znaci za [latex]r = 1 + cos(3\phi)[/latex]:
Najbolje je pogledati kad funkcije mjenja iz padajuce u rastucu ( i obrnuto ), znaci to je za [latex]f(x) = 1 + cos(3 x)[/latex] svakih [latex]\frac \pi 3[/latex].
Nacrtamo pomocni graf [latex]f(x)[/latex] u kartezijev koordinatama.
Nactramo graf u polarnim koodrinatama i oznacimo "kriticne" kuteve ([latex]0, \frac \pi 3, 2 \frac \pi 3, ..., 2 \pi[/latex])
U [latex]f(0)=2 = r[/latex], u [latex]f(\frac \pi 3) = 0 = r[/latex], ljepse receno graf [latex]f(x)[/latex] je u 0 jednak 2 i onda do [latex]\frac \pi 3[/latex] pada u 0 (koristimo pomocni graf da sve jos ljepse vidimo). Pa nacrtamo to. Nadalje za [latex]f(2 \frac \pi 3)= 2 = r[/latex]. Znaci da od [latex]\frac \pi 3[/latex] do [latex]2 \frac \pi 3[/latex] raste do 2. Za [latex]f(\pi)= 0 = r[/latex] pa analogno graf opet pada u 0 (r je udaljenost od ishodista). I sad mozemo iskoristi simetricnost cos preko x osi i dobimo lijepi graf.
Do sada su mi sve dobri grafovi ispali, nemogu garantirati za ne lijepe funkcije :D
Mozda ovo nekome pomogne 
Znaci za 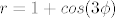 : :
Najbolje je pogledati kad funkcije mjenja iz padajuce u rastucu ( i obrnuto ), znaci to je za 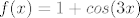 svakih svakih 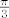 . .
Nacrtamo pomocni graf 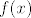 u kartezijev koordinatama. u kartezijev koordinatama.
Nactramo graf u polarnim koodrinatama i oznacimo "kriticne" kuteve (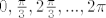 ) )
U 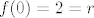 , u , u  , ljepse receno graf , ljepse receno graf 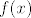 je u 0 jednak 2 i onda do je u 0 jednak 2 i onda do 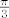 pada u 0 (koristimo pomocni graf da sve jos ljepse vidimo). Pa nacrtamo to. Nadalje za pada u 0 (koristimo pomocni graf da sve jos ljepse vidimo). Pa nacrtamo to. Nadalje za 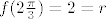 . Znaci da od . Znaci da od 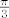 do do 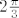 raste do 2. Za raste do 2. Za 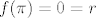 pa analogno graf opet pada u 0 (r je udaljenost od ishodista). I sad mozemo iskoristi simetricnost cos preko x osi i dobimo lijepi graf. pa analogno graf opet pada u 0 (r je udaljenost od ishodista). I sad mozemo iskoristi simetricnost cos preko x osi i dobimo lijepi graf.
Do sada su mi sve dobri grafovi ispali, nemogu garantirati za ne lijepe funkcije 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:04 pon, 6. 6. 2011 Naslov: Postano: 10:04 pon, 6. 6. 2011 Naslov: |
    |
|
|
Dobivamo da su krivulje koje omeđuju ovaj lik zadane s [latex]\displaystyle y=\pm 4(1-(\frac{x}{5})^2)^(3/2)[/latex], zar ne? (Čisto izrazimo [latex]y[/latex] preko iksa.)
Očito, ta površina "počinje" u [latex]x=-5[/latex], a "završava" u [latex]x=5[/latex]. (Tada je [latex]\displaystyle (\frac{x}{5})^2=1[/latex].)
Ova krivulja s minusom ispred sebe je očito manja, pa po poznatoj formuli za površinu, zapravo želimo integrirati [latex]4(1-(\frac{x}{5})^2)^(3/2)- (-4(1-(\frac{x}{5})^2)^(3/2))=8(1-(\frac{x}{5})^2)^(3/2)[/latex] po [latex]\left[-5,5\right][/latex].
To ne bi trebalo biti preteško - radi se o tradicionalnoj trigonometrijskoj supstituciji [latex]x=5\sin t[/latex]. Dobivamo da želimo integrirati [latex]8(1-\sin^2(t))^{3/2}\cdot 5\cdot \cos t[/latex] od [latex]-\pi/2[/latex] do [latex]\pi/2[/latex]. E, a to je [latex]40\cos^4 t[/latex]. Sad samo preostaje integrirati [latex]\cos^4 t[/latex], a to se radi, u nekom trenutku, negdje. :) (Ne budem lijen, išao sam pogledati - međurezultat iz 2.43. d) je u pitanju. :))
Eto, to bi valjda bilo to. Odgovor je navodno negdje [latex]15\pi[/latex]. :)
Dobivamo da su krivulje koje omeđuju ovaj lik zadane s 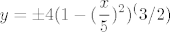 , zar ne? (Čisto izrazimo , zar ne? (Čisto izrazimo  preko iksa.) preko iksa.)
Očito, ta površina "počinje" u  , a "završava" u , a "završava" u  . (Tada je . (Tada je 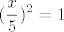 .) .)
Ova krivulja s minusom ispred sebe je očito manja, pa po poznatoj formuli za površinu, zapravo želimo integrirati 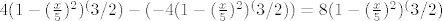 po po 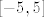 . .
To ne bi trebalo biti preteško - radi se o tradicionalnoj trigonometrijskoj supstituciji 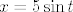 . Dobivamo da želimo integrirati . Dobivamo da želimo integrirati 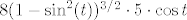 od od 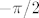 do do 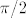 . E, a to je . E, a to je 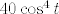 . Sad samo preostaje integrirati . Sad samo preostaje integrirati 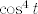 , a to se radi, u nekom trenutku, negdje. , a to se radi, u nekom trenutku, negdje.  (Ne budem lijen, išao sam pogledati - međurezultat iz 2.43. d) je u pitanju. (Ne budem lijen, išao sam pogledati - međurezultat iz 2.43. d) je u pitanju.  ) )
Eto, to bi valjda bilo to. Odgovor je navodno negdje 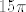 . . 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
|









