| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
borobortic
Forumaš(ica)

Pridružen/a: 03. 06. 2011. (19:02:38)
Postovi: (7)16
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 19:20 pon, 6. 6. 2011 Naslov: Postano: 19:20 pon, 6. 6. 2011 Naslov: |
    |
|
|
[quote="borobortic"]Ljudi, moze pomoc oko jedne sitnice...
Zašto je QXQ podskup od RXQ, a nije podskup od QXR?
To je onaj zadatak iz vjezbi QXR i RXQ nisu slicni...
Zar ne postoji uvijek bijekcija izmedu takvih skupova:
f(a,b) = (b,a) ???[/quote]
Želi se dokazat da su oba ova skupa slična sa R ( s obzirom da im je kardinalnost jednaka c ).
Mislim da se sličnost ovdje "ruši" onim svojstvom ( ne znam kak se točno zove ) da u RXQ postoji prebrojiv podskup koji je gust u RXQ, dok takav ne postoji u QXR, tj. kada bi takav postojao onda bi posebno između svaka dva elementa iz QXR morao postojati barem jedan element iz tog prebrojivog skupa.
Pa bi posbno to moralo vrijediti i za npr sve elemente tipa:
(1,x) i (2,x) ( međutim x ovdje varira po R ), pa bi dobio da taj skup ima elemenata najmanje kao i R, tj. taj skup bi bio neprebrojiv ( a ne prebrojiv ) i tu se dobije da nisu slični ( bijekcija postoji, ali ne postoji sličnost koja ima veze s ovim zadatkom ).
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="Vip"]jel može pomoć oko dokaza jesu li [latex]Q^+ \times Q^- , Q_0^+ \times N[/latex] slični skupovi?[/quote]
Ne znam dal se smije koristiti na kolokviju, no i ako se ne može nije veliki problem za dokazat da je postojanje minimalnog, maximalnog, najmanjeg ili najvećeg elementa invarijanta sličnosti, tj. Ako neki skup ima najmanji element, onda ga ima i svaki skup koji je njemu sličan.
u skupu [latex] Q_0^+ \times N[/latex] je najmanji element (0,0)
dok u [latex]Q^+ \times Q^-[/latex] nema najmanjeg elementa.
( Treba to malo raspisat )
| borobortic (napisa): | Ljudi, moze pomoc oko jedne sitnice...
Zašto je QXQ podskup od RXQ, a nije podskup od QXR?
To je onaj zadatak iz vjezbi QXR i RXQ nisu slicni...
Zar ne postoji uvijek bijekcija izmedu takvih skupova:
f(a,b) = (b,a) ??? |
Želi se dokazat da su oba ova skupa slična sa R ( s obzirom da im je kardinalnost jednaka c ).
Mislim da se sličnost ovdje "ruši" onim svojstvom ( ne znam kak se točno zove ) da u RXQ postoji prebrojiv podskup koji je gust u RXQ, dok takav ne postoji u QXR, tj. kada bi takav postojao onda bi posebno između svaka dva elementa iz QXR morao postojati barem jedan element iz tog prebrojivog skupa.
Pa bi posbno to moralo vrijediti i za npr sve elemente tipa:
(1,x) i (2,x) ( međutim x ovdje varira po R ), pa bi dobio da taj skup ima elemenata najmanje kao i R, tj. taj skup bi bio neprebrojiv ( a ne prebrojiv ) i tu se dobije da nisu slični ( bijekcija postoji, ali ne postoji sličnost koja ima veze s ovim zadatkom ).
Added after 3 minutes:
| Vip (napisa): | jel može pomoć oko dokaza jesu li 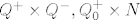 slični skupovi? slični skupovi? |
Ne znam dal se smije koristiti na kolokviju, no i ako se ne može nije veliki problem za dokazat da je postojanje minimalnog, maximalnog, najmanjeg ili najvećeg elementa invarijanta sličnosti, tj. Ako neki skup ima najmanji element, onda ga ima i svaki skup koji je njemu sličan.
u skupu 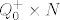 je najmanji element (0,0) je najmanji element (0,0)
dok u 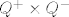 nema najmanjeg elementa. nema najmanjeg elementa.
( Treba to malo raspisat )
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
slash
Forumaš(ica)
Pridružen/a: 20. 02. 2008. (18:17:24)
Postovi: (39)16
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 19:04 uto, 7. 6. 2011 Naslov: Postano: 19:04 uto, 7. 6. 2011 Naslov: |
    |
|
|
[quote="slash"]jel bi netko mogao pomoc oko 4. i 6. zdk sa proslogodisnjeg kolokvija?
4. TUS je okrenut nagore ako u njemu postoji strogo rastuci niz. Dokazite da je okrenutost nagore invarijanta slicnosti.
6. neka je A podskp od [0,1] dobro uređen restrikcijom standardnog uređaja na R. Moze li A biti neprebrojiv? Dokazite.[/quote]
Ja cu rijesit 6ti, a 4ti ce Ana i Jele :P, koje kazu da im je to lako :)
Dakle, 6ti. Pp. da je A neprebrojiv. Jer je A DUS onda svaki element (osim maksimalnog, ako imam maksimalni) ima neposrednog slijedbenika. Definiram funkciju f:A*->Q td. f(a) je neki racionalan broj iz intervala <a,sljedbenik od a> gdje je A*=A\{maksimalni element}, odnosno A*=A ako takvog nema. Jasno je da je i A* neprebrojiv. Ocito je f injekcija sa A* u Q pa je to kontradikcija s neprebrojivoscu od A*.
| slash (napisa): | jel bi netko mogao pomoc oko 4. i 6. zdk sa proslogodisnjeg kolokvija?
4. TUS je okrenut nagore ako u njemu postoji strogo rastuci niz. Dokazite da je okrenutost nagore invarijanta slicnosti.
6. neka je A podskp od [0,1] dobro uređen restrikcijom standardnog uređaja na R. Moze li A biti neprebrojiv? Dokazite. |
Ja cu rijesit 6ti, a 4ti ce Ana i Jele  , koje kazu da im je to lako , koje kazu da im je to lako 
Dakle, 6ti. Pp. da je A neprebrojiv. Jer je A DUS onda svaki element (osim maksimalnog, ako imam maksimalni) ima neposrednog slijedbenika. Definiram funkciju f:A*→Q td. f(a) je neki racionalan broj iz intervala <a,sljedbenik od a> gdje je A*=A\{maksimalni element}, odnosno A*=A ako takvog nema. Jasno je da je i A* neprebrojiv. Ocito je f injekcija sa A* u Q pa je to kontradikcija s neprebrojivoscu od A*.
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
slash
Forumaš(ica)
Pridružen/a: 20. 02. 2008. (18:17:24)
Postovi: (39)16
|
 Postano: 19:15 uto, 7. 6. 2011 Naslov: Postano: 19:15 uto, 7. 6. 2011 Naslov: |
    |
|
|
novi hvala :)
ddddddu imam ih na papiru.
ako te zanima koji su: 1-3 teorija, 5. vec ima na forumu(ono sa slicnosti), 7. izracunaj: (w+2)(w+3)(w+4), 8. dokazite da postoji maksimalan neprazan skup S u ravnini, sa svojstvom da za svake dvije tocke A,B iz S, skup S sadrzi poloviste duzine AB, te da S ne sadrzi niijednu tocku s cjelobrojnim koordinatama.
novi hvala 
ddddddu imam ih na papiru.
ako te zanima koji su: 1-3 teorija, 5. vec ima na forumu(ono sa slicnosti), 7. izracunaj: (w+2)(w+3)(w+4), 8. dokazite da postoji maksimalan neprazan skup S u ravnini, sa svojstvom da za svake dvije tocke A,B iz S, skup S sadrzi poloviste duzine AB, te da S ne sadrzi niijednu tocku s cjelobrojnim koordinatama.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 21:20 uto, 7. 6. 2011 Naslov: Postano: 21:20 uto, 7. 6. 2011 Naslov: |
    |
|
|
Mogu ja 4.? :D
Dakle,u tus-u su svi elementi usporedivi, pa možemo napisati da je taj niz npr. x0<x1<...<xn.
Tvrdimo da je f(x0)<f(x1)<...f(xn) rastući niz. Pretp.suprotno,tj. postoji i,j td f(xi)<f(y)>f(xj), (to je jedan slučaj,ali mislim da je BSO),tj. taj niz nije strogo rastući. Sada primjenimo inverznu f-ju koja također čuva uređaj i dobimo da postoji y iz našeg niza t.d. xi<y>xj,što je kontradikcija.
Ja se nadam da je to ok,iako nisam baš išla u detalje :oops:
Mogu ja 4.? 
Dakle,u tus-u su svi elementi usporedivi, pa možemo napisati da je taj niz npr. x0<x1<...<xn.
Tvrdimo da je f(x0)<f(x1)<...f(xn) rastući niz. Pretp.suprotno,tj. postoji i,j td f(xi)<f(y)>f(xj), (to je jedan slučaj,ali mislim da je BSO),tj. taj niz nije strogo rastući. Sada primjenimo inverznu f-ju koja također čuva uređaj i dobimo da postoji y iz našeg niza t.d. xi<y>xj,što je kontradikcija.
Ja se nadam da je to ok,iako nisam baš išla u detalje 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 21:28 uto, 7. 6. 2011 Naslov: Postano: 21:28 uto, 7. 6. 2011 Naslov: |
    |
|
|
f sličnost
x_n niz
x_i < x_i+1
pretp da f (x_i) > f (x_i+1)
f^-1 također čuva uređaj
hazza! x_i > x_i+1 kontradikcija s x_i < x_i+1
[size=7]nije mi se dalo stisnit latex dugme [/size]
f sličnost
x_n niz
x_i < x_i+1
pretp da f (x_i) > f (x_i+1)
f^-1 također čuva uređaj
hazza! x_i > x_i+1 kontradikcija s x_i < x_i+1
nije mi se dalo stisnit latex dugme
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Mrs. Bean
Forumaš(ica)

Pridružen/a: 29. 06. 2009. (22:03:56)
Postovi: (31)16
Spol: 
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
borobortic
Forumaš(ica)

Pridružen/a: 03. 06. 2011. (19:02:38)
Postovi: (7)16
|
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
borobortic
Forumaš(ica)

Pridružen/a: 03. 06. 2011. (19:02:38)
Postovi: (7)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
|













