| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 12:33 pet, 24. 6. 2011 Naslov: Postano: 12:33 pet, 24. 6. 2011 Naslov: |
    |
|
|
Trebaš provjeriti da li vrijedi
[latex]\varphi(~(x_1,y_1,z_1)+(x_2,y_2,z_2)~)=\varphi((x_1,y_1,z_1))+\varphi((x_2,y_2,z_2))[/latex]
Jer je [latex](x_1,y_1,z_1)+(x_2,y_2,z_2)=(x_1+x_2,y_1+y_2,z_1+z_2)[/latex], uvrštavanjem u [latex]\varphi[/latex] i računanjem se vidi da je to homomorfizam.
Jezgra će biti podskup od Z^3 td. je 3x+5y-z=0 i x+z=0, a slika će biti cijeli Z^2 jer [latex]\varphi(4,-3,-4)=(1,0)[/latex] i [latex]\varphi(4,-3,-3)=(0,1)[/latex], a {(1,0),(0,1)} je baza za Z^2.
Trebaš provjeriti da li vrijedi
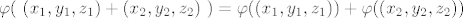
Jer je 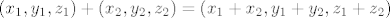 , uvrštavanjem u , uvrštavanjem u 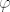 i računanjem se vidi da je to homomorfizam. i računanjem se vidi da je to homomorfizam.
Jezgra će biti podskup od Z^3 td. je 3x+5y-z=0 i x+z=0, a slika će biti cijeli Z^2 jer 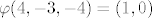 i i 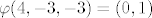 , a {(1,0),(0,1)} je baza za Z^2. , a {(1,0),(0,1)} je baza za Z^2.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 12:56 pet, 24. 6. 2011 Naslov: Postano: 12:56 pet, 24. 6. 2011 Naslov: |
    |
|
|
[quote="goranm"]
Jezgra će biti podskup od Z^3 td. je 3x+5y-z=0 i x+z=0, a slika će biti cijeli Z^2 jer [latex]\varphi(4,-3,-4)=(1,0)[/latex] i [latex]\varphi(4,-3,-3)=(0,1)[/latex], a {(1,0),(0,1)} je baza za Z^2.[/quote]
Ok prvi dio sam shvatio, kao i jezgru...
Ali kako si ti dobio ove vektore [latex](4,-3,4)[/latex] i [latex](4,-3,-3)[/latex] i zasto je cijeli [latex]Z^2[/latex] Im, ako ta dva vektora [latex](4,-3,4)[/latex] i [latex](4,-3,-3)[/latex] kada djelujemo na njega [latex]\varphi[/latex] cine bazu
| goranm (napisa): |
Jezgra će biti podskup od Z^3 td. je 3x+5y-z=0 i x+z=0, a slika će biti cijeli Z^2 jer 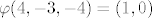 i i 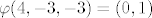 , a {(1,0),(0,1)} je baza za Z^2. , a {(1,0),(0,1)} je baza za Z^2. |
Ok prvi dio sam shvatio, kao i jezgru...
Ali kako si ti dobio ove vektore 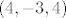 i i 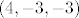 i zasto je cijeli i zasto je cijeli 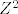 Im, ako ta dva vektora Im, ako ta dva vektora 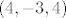 i i 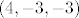 kada djelujemo na njega kada djelujemo na njega 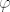 cine bazu cine bazu
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:14 pet, 24. 6. 2011 Naslov: Postano: 13:14 pet, 24. 6. 2011 Naslov: |
    |
|
|
Vektor (4,-3,-4) sam dobio tako što sam riješio sustav
3x+5y-z=1
x+z=0
Rješenje tog sustava je [latex](\frac{1-5y}{4},y,-\frac{1-5y}{4})[/latex] i onda sam uzeo prvi y koji mi je pao napamet tako da (1-5y)/4 bude cijeli broj. Analogno za drugi vektor.
Slika će biti cijeli Z^2 jer ako uzmemo (a,b) iz Z^2, onda je
[latex](a,b)=a(1,0)+b(0,1)=\underbrace{(1,0)+\cdots +(1,0)}_{a~puta}+\underbrace{(0,1)+\cdots +(0,1)}_{b~puta}=\\
\underbrace{\varphi (4,-3,-4)+\cdots+\varphi (4,-3,-4)}_{a~puta}+\underbrace{\varphi(4,-3,-3)+\cdots +\varphi(4,-3,-3)}_{b~puta}=\\
\varphi(a(4,-3,-4)+b(4,-3,-3))=\varphi(4a+4b,-3a-3b,-4a-3b),
[/latex]
tj. za svaki (a,b) iz Z^2 postoji (x,y,z) iz Z^3 tako da je se (x,y,z) preslikava u (a,b).
To sve slijedi iz definicije homomorfizma grupa i generatora grupe i općenito vrijedi da ako homomorfizam preslikava neke elemente domene u bazu kodomene, onda će ujedno biti i epimorfizam.
Vektor (4,-3,-4) sam dobio tako što sam riješio sustav
3x+5y-z=1
x+z=0
Rješenje tog sustava je 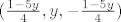 i onda sam uzeo prvi y koji mi je pao napamet tako da (1-5y)/4 bude cijeli broj. Analogno za drugi vektor. i onda sam uzeo prvi y koji mi je pao napamet tako da (1-5y)/4 bude cijeli broj. Analogno za drugi vektor.
Slika će biti cijeli Z^2 jer ako uzmemo (a,b) iz Z^2, onda je
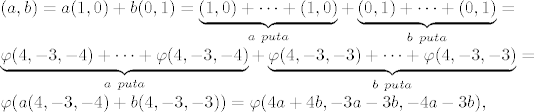
tj. za svaki (a,b) iz Z^2 postoji (x,y,z) iz Z^3 tako da je se (x,y,z) preslikava u (a,b).
To sve slijedi iz definicije homomorfizma grupa i generatora grupe i općenito vrijedi da ako homomorfizam preslikava neke elemente domene u bazu kodomene, onda će ujedno biti i epimorfizam.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Gost
|
 Postano: 10:23 pet, 1. 7. 2011 Naslov: Postano: 10:23 pet, 1. 7. 2011 Naslov: |
    |
|
|
S= Q presjek (0, +besk) defi, binarnu operaciju * ovako: x*y= 3xy, za svaki x,y is S. Evo, moze i ovaj primjer
S= Q presjek (0, +besk) defi, binarnu operaciju * ovako: x*y= 3xy, za svaki x,y is S. Evo, moze i ovaj primjer
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:22 pet, 1. 7. 2011 Naslov: Postano: 11:22 pet, 1. 7. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]S= Q presjek (0, +besk) defi, binarnu operaciju * ovako: x*y= 3xy, za svaki x,y is S. Evo, moze i ovaj primjer[/quote]
Imaš zadan skup i operaciju; i definiciju grupoida. Gdje si zapeo/la u provjeri po definiciji?
| Anonymous (napisa): | | S= Q presjek (0, +besk) defi, binarnu operaciju * ovako: x*y= 3xy, za svaki x,y is S. Evo, moze i ovaj primjer |
Imaš zadan skup i operaciju; i definiciju grupoida. Gdje si zapeo/la u provjeri po definiciji?
|
|
| [Vrh] |
|
Gost
|
 Postano: 11:36 pet, 1. 7. 2011 Naslov: Postano: 11:36 pet, 1. 7. 2011 Naslov: |
    |
|
|
[quote="rafaelm"][quote="Anonymous"]S= Q presjek (0, +besk) defi, binarnu operaciju * ovako: x*y= 3xy, za svaki x,y is S. Evo, moze i ovaj primjer[/quote]
Imaš zadan skup i operaciju; i definiciju grupoida. Gdje si zapeo/la u provjeri po definiciji?[/quote]
(x1,y1)*(x2,y2)=3(x1,x2)(y1,y2)=3x1y13x2y2..
Jel to tak ide?
| rafaelm (napisa): | | Anonymous (napisa): | | S= Q presjek (0, +besk) defi, binarnu operaciju * ovako: x*y= 3xy, za svaki x,y is S. Evo, moze i ovaj primjer |
Imaš zadan skup i operaciju; i definiciju grupoida. Gdje si zapeo/la u provjeri po definiciji? |
(x1,y1)*(x2,y2)=3(x1,x2)(y1,y2)=3x1y13x2y2..
Jel to tak ide?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|












