| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Charmed
Forumaš(ica)


Pridružen/a: 22. 02. 2009. (11:51:49)
Postovi: (20B)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:02 čet, 10. 6. 2010 Naslov: Postano: 19:02 čet, 10. 6. 2010 Naslov: |
    |
|
|
[quote]I kakva je točno povezanost konvergencije L1 i konvergencije po mjeri ?[/quote]
Konvergencija u [latex]L^p,~p>0[/latex] povlači konvergenciju po mjeri, ali obrat ne vrijedi niti za jedan p>0.
[quote](Jer u zadacima sa vježbi negdje smo rekli da po mjeri => L1 ali obrat ne vrijedi?)[/quote]
Obratno je. Npr. niz [latex]f_n=n \cdot 1_{[\frac{1}{n},\frac{2}{n}]}[/latex] konvergira skoro svuda prema 0 i definiran je na prostoru konačne mjere pa konvergira i po Lebesgueovoj mjeri, ali ne konvergira u [latex]L^p[/latex]. Specijalno, za p=1, kada bi taj niz konvergirao u [latex]L^1[/latex], morao bi konvergirati ka istom limesu kao i kod s.s. konvergencije, tj. prema 0. Ali
[latex]||f_n-0||_1=\int |f_n| d\lambda=n\int 1_{[\frac{1}{n},\frac{2}{n}]}d\lambda=n\lambda([\frac{1}{n},\frac{2}{n}])=n\cdot \frac{1}{n}=1 \neq 0.[/latex]
| Citat: | | I kakva je točno povezanost konvergencije L1 i konvergencije po mjeri ? |
Konvergencija u 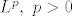 povlači konvergenciju po mjeri, ali obrat ne vrijedi niti za jedan p>0. povlači konvergenciju po mjeri, ali obrat ne vrijedi niti za jedan p>0.
| Citat: | | (Jer u zadacima sa vježbi negdje smo rekli da po mjeri ⇒ L1 ali obrat ne vrijedi?) |
Obratno je. Npr. niz 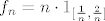 konvergira skoro svuda prema 0 i definiran je na prostoru konačne mjere pa konvergira i po Lebesgueovoj mjeri, ali ne konvergira u konvergira skoro svuda prema 0 i definiran je na prostoru konačne mjere pa konvergira i po Lebesgueovoj mjeri, ali ne konvergira u  . Specijalno, za p=1, kada bi taj niz konvergirao u . Specijalno, za p=1, kada bi taj niz konvergirao u  , morao bi konvergirati ka istom limesu kao i kod s.s. konvergencije, tj. prema 0. Ali , morao bi konvergirati ka istom limesu kao i kod s.s. konvergencije, tj. prema 0. Ali

_________________
The Dude Abides
|
|
| [Vrh] |
|
Charmed
Forumaš(ica)


Pridružen/a: 22. 02. 2009. (11:51:49)
Postovi: (20B)16
Spol: 
|
|
| [Vrh] |
|
Charmed
Forumaš(ica)


Pridružen/a: 22. 02. 2009. (11:51:49)
Postovi: (20B)16
Spol: 
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
 Postano: 8:40 pon, 5. 7. 2010 Naslov: Postano: 8:40 pon, 5. 7. 2010 Naslov: |
    |
|
|
Oznaci [latex]A_n=<1-\frac1n,1>[/latex], onda je [latex]f_n=1_{A_n}[/latex]. Primijeti da je [latex]A_n \subseteq <0,1>[/latex], pa zato [latex]x \not \in <0,1> \Rightarrow x \not \in A_n[/latex]. Sad vidis da je [latex]f_n(x)=0, \forall x \in \mathbb{R} \setminus <0,1>[/latex]. Dakle to je ono [latex]x \geq 1[/latex] i [latex]x\leq 0[/latex]. A sad uzmimo proizvoljni [latex]x \in <0,1>[/latex]. Posto je [latex]1-\frac1n[/latex] rastuci niz s limesom [latex]1[/latex], postoji [latex]n \in \mathbb{N}[/latex] takav da je [latex]1-\frac1n>x[/latex], te je sada ocito [latex]f_n(x)=0[/latex], pa [latex]f_n[/latex] konvergira u nul-funkciju po tockama, dakle i [latex]\mu-s.s[/latex].
Oznaci 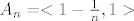 , onda je , onda je  . Primijeti da je . Primijeti da je 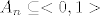 , pa zato , pa zato 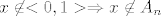 . Sad vidis da je . Sad vidis da je 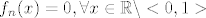 . Dakle to je ono . Dakle to je ono 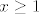 i i  . A sad uzmimo proizvoljni . A sad uzmimo proizvoljni  . Posto je . Posto je  rastuci niz s limesom rastuci niz s limesom  , postoji , postoji  takav da je takav da je  , te je sada ocito , te je sada ocito 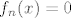 , pa , pa 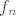 konvergira u nul-funkciju po tockama, dakle i konvergira u nul-funkciju po tockama, dakle i 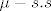 . .
|
|
| [Vrh] |
|
Charmed
Forumaš(ica)


Pridružen/a: 22. 02. 2009. (11:51:49)
Postovi: (20B)16
Spol: 
|
|
| [Vrh] |
|
Zvjezdica
Forumaš(ica)

Pridružen/a: 02. 07. 2009. (12:40:02)
Postovi: (58)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:00 ned, 5. 6. 2011 Naslov: Postano: 16:00 ned, 5. 6. 2011 Naslov: |
    |
|
|
Najprije da ti pokušam razjasniti pojmove konvergencije, u pravu si kad si rekla da uniformna konvergencija povlači konvergenciju po točkama, no, to ne znači da ako nešto konvergira po točkama konvergira i uniformno. Zamisli da u ovom trenutku znaš da ćeš sigurno proći mjeru ovaj semestar, bila bi sretna, jel tako? No, ukoliko si sretna u ovom trenutku, to ne znači da ćeš sigurno proći mjeru, ima logike, zar ne?
Dakle, ako nešto konvergira uniformno, onda to konvergira i po točkama, obratno, općenito, NE VRIJEDI. Točnije, može konvergirati po točkama, ali ne mora uniformno i primjer koji si navela nam točno to i pokazuje.
Evo što vrijedi, opet, samo u navedenim smjerovima, obrati, općenito, NE VRIJEDE! :)
UNIFORMNA KONVERGENCIJA ----> KONVERGENCIJA PO TOČKAMA ----> KONVERGENCIJA [latex]\mu[/latex] - s.s.
Nadalje;
UNIFORMA KONVERGENCIJA ----> KONVERGENCIJA PO MJERI
KONVERGENCIJA U SREDNJEM REDA [latex]p[/latex] (Odnosno, konvergencija u [latex]L^p[/latex].) ----> KONVERGENCIJA PO MJERI
KONVERGENCIJA [latex]\mu[/latex] - s.s. + mjera je konačna ----> KONVERGENCIJA PO MJERI
KONVERGENCIJA PO MJERI ----> postoji podniz koji KONVERGIRA [latex]\mu[/latex] - s.s.
Na kraju, odglumiti ću dobru dušu i raspisati ove zadatke koje si napisala.
Najprije uočimo da sva tri tipa navedenih funkcija egzistiraju samo na skupu [latex]\left\langle 0,\, 1 \right\rangle[/latex]. Pretpostavljam da gledamo Lebesgueovu mjeru, stoga vidimo da radimo na prostoru konačne mjere, točnije, na prostoru mjere [latex]\lambda\left(\left\langle 0,\, 1 \right\rangle\right)=1[/latex].
Pokažimo najprije da sva tri niza konvergiraju po točkama ka nul funkciji. Što će nam odmah reći da konvergiraju i [latex]\mu[/latex] - s.s. prema nul funkciji, a pošto je prostor konačne mjere, konvergiraju i po mjeri ka nul funkciji.
Neka je [latex]x \in \left\langle 0,\, 1 \right\rangle[/latex].
1.) Prema Arhimedovom aksiomu postoji dovoljno velik [latex]n_0 \in \mathbb{N}[/latex] takav da je [latex]1 - \frac{1}{n} > x[/latex] za svaki [latex]n \in \mathbb{N},\ n \geq n_0[/latex], odnosno, [latex]f_n\left(x\right)=0,\ \forall n \in \mathbb{N},\ n \geq n_0[/latex], dakle, zadani niz konvergira po točkama prema nul funkciji.
2.) Samo primijetimo da [latex]\frac{1}{n} \to 0[/latex] kada [latex]n \to +\infty[/latex].
3.) Potpuno ista argumentacija kao u 1.).
Ostaje nam još za ispitati uniformnu konvergenciju i konvergenciju u srednjem reda [latex]p[/latex]. To mi se trenutno ne da pisati, ako bude problema javi pa ću i to raspisati! :)
Najprije da ti pokušam razjasniti pojmove konvergencije, u pravu si kad si rekla da uniformna konvergencija povlači konvergenciju po točkama, no, to ne znači da ako nešto konvergira po točkama konvergira i uniformno. Zamisli da u ovom trenutku znaš da ćeš sigurno proći mjeru ovaj semestar, bila bi sretna, jel tako? No, ukoliko si sretna u ovom trenutku, to ne znači da ćeš sigurno proći mjeru, ima logike, zar ne?
Dakle, ako nešto konvergira uniformno, onda to konvergira i po točkama, obratno, općenito, NE VRIJEDI. Točnije, može konvergirati po točkama, ali ne mora uniformno i primjer koji si navela nam točno to i pokazuje.
Evo što vrijedi, opet, samo u navedenim smjerovima, obrati, općenito, NE VRIJEDE! 
UNIFORMNA KONVERGENCIJA ----> KONVERGENCIJA PO TOČKAMA ----> KONVERGENCIJA 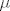 - s.s. - s.s.
Nadalje;
UNIFORMA KONVERGENCIJA ----> KONVERGENCIJA PO MJERI
KONVERGENCIJA U SREDNJEM REDA  (Odnosno, konvergencija u (Odnosno, konvergencija u  .) ----> KONVERGENCIJA PO MJERI .) ----> KONVERGENCIJA PO MJERI
KONVERGENCIJA 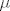 - s.s. + mjera je konačna ----> KONVERGENCIJA PO MJERI - s.s. + mjera je konačna ----> KONVERGENCIJA PO MJERI
KONVERGENCIJA PO MJERI ----> postoji podniz koji KONVERGIRA 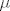 - s.s. - s.s.
Na kraju, odglumiti ću dobru dušu i raspisati ove zadatke koje si napisala.
Najprije uočimo da sva tri tipa navedenih funkcija egzistiraju samo na skupu 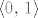 . Pretpostavljam da gledamo Lebesgueovu mjeru, stoga vidimo da radimo na prostoru konačne mjere, točnije, na prostoru mjere . Pretpostavljam da gledamo Lebesgueovu mjeru, stoga vidimo da radimo na prostoru konačne mjere, točnije, na prostoru mjere 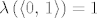 . .
Pokažimo najprije da sva tri niza konvergiraju po točkama ka nul funkciji. Što će nam odmah reći da konvergiraju i 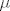 - s.s. prema nul funkciji, a pošto je prostor konačne mjere, konvergiraju i po mjeri ka nul funkciji. - s.s. prema nul funkciji, a pošto je prostor konačne mjere, konvergiraju i po mjeri ka nul funkciji.
Neka je 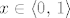 . .
1.) Prema Arhimedovom aksiomu postoji dovoljno velik  takav da je takav da je  za svaki za svaki 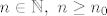 , odnosno, , odnosno, 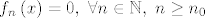 , dakle, zadani niz konvergira po točkama prema nul funkciji. , dakle, zadani niz konvergira po točkama prema nul funkciji.
2.) Samo primijetimo da 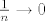 kada kada 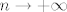 . .
3.) Potpuno ista argumentacija kao u 1.).
Ostaje nam još za ispitati uniformnu konvergenciju i konvergenciju u srednjem reda  . To mi se trenutno ne da pisati, ako bude problema javi pa ću i to raspisati! . To mi se trenutno ne da pisati, ako bude problema javi pa ću i to raspisati! 
|
|
| [Vrh] |
|
Zvjezdica
Forumaš(ica)

Pridružen/a: 02. 07. 2009. (12:40:02)
Postovi: (58)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:29 ned, 5. 6. 2011 Naslov: Postano: 20:29 ned, 5. 6. 2011 Naslov: |
    |
|
|
[quote="Zvjezdica"]Sad kada provjeravamo uniformnu konvergenciju kao kandidata uvijek uzimamo f(x)=0? (to zaključujemo po? )[/quote]
Recimo da provjeravaš tipove konvergencije A i B te neka vrijedi da tip konvergencije A povlači tip konvergencije B. (Obratno ne nužno!)
Ako si pokazala da niz funkcija konvergira u tipu konvergencije B prema funkciji [latex]f[/latex] onda je jasno da ako konvergira u tiipu konvergencije A da to mora biti prema istoj funkciji [latex]f[/latex]. Naime, ukoliko bi u tipu konvergencije A konvergirao prema nekoj drugoj funkciji [latex]g[/latex], onda, pošto tip konvergencije A povlači tip konvergencije B, dobivamo da i u tipu konvergencije B konvergira prema [latex]g[/latex], a to je kontradikcija s tim da u tipu konvergencije B konvergira prema [latex]f[/latex].
Dakle, kod provjeravanja bilo kojeg od 5 tipova konvergencije, ako pokažeš da u jednom od njih konvergira prema [latex]f[/latex] onda znaš da u svima ostalima, ako u njima konvergira, mora konvergirati prema istom tom [latex]f[/latex].
[quote="Zvjezdica"]E i još kod ove provjere po točkama, ako vidimo da je [latex]f_n[/latex]oblika 1/nešto, možemo zaključiti da konvergira prema 0 za [latex]n \to +\infty[/latex] i ne trebamo dalje provjeravati?[/quote]
Rekao bih da da, naravno, moraš paziti da to nešto ovisi o [latex]n[/latex] i da to nešto teži u ful puno kako [latex]n[/latex] teži u ful puno i to za svaki fiksni [latex]x[/latex] iz domene. Normalno, to u slučaju da provjeravaš točkovnu konvergenciju.
[quote="Zvjezdica"]Kod primjera
[latex]f_{n}=\frac{1}{n}\ 1_{<0,n>}[/latex]
napisali smo za konvergenciju po mjeri
[latex]\lambda \{x \in X : |\frac{1}{n}\ 1_{<0,n>}| > \epsilon \} = \lambda (O)=0[/latex]
Zašto prazan skup a ne 1? mislim opet ispada [latex]\lambda (1)=0[/latex][/quote]
Pretpostavljam da ti nedostaje limes, evo, napisati ću sve lijepo! :)
Neka je [latex]\varepsilon > 0[/latex], za svaki [latex]n \in \mathbb{N}[/latex] definirajmo
[latex]A_n := \left\{x \in \mathbb{R} : \left|f_n\left(x\right)\right| > \varepsilon\right\}.[/latex]
Opet koristimo Arhimedov akisom prema kojem znamo da postoji dovoljno velik [latex]n_0 \in \mathbb{N}[/latex] takav da je [latex]\frac{1}{n} \leq \varepsilon,\ \forall n \in \mathbb{N},\ n \geq n_0[/latex]. Dakle, za svaki [latex]n \in \mathbb{N},\ n \geq n_0[/latex] je [latex]A_n = \emptyset[/latex]. Konačno, za svaki [latex]\varepsilon > 0[/latex] dobivamo da je
[latex]\lim\limits_{n \to +\infty} \lambda\left(A_n\right) = \lim\limits_{n \to +\infty,\ n \geq n_0} \lambda\left(A_n\right) = \lim\limits_{n \to +\infty}\lambda\left(\emptyset\right) = 0[/latex].
Eto ga, nadam se da je sve razjašnjeno! :)
| Zvjezdica (napisa): | | Sad kada provjeravamo uniformnu konvergenciju kao kandidata uvijek uzimamo f(x)=0? (to zaključujemo po? ) |
Recimo da provjeravaš tipove konvergencije A i B te neka vrijedi da tip konvergencije A povlači tip konvergencije B. (Obratno ne nužno!)
Ako si pokazala da niz funkcija konvergira u tipu konvergencije B prema funkciji  onda je jasno da ako konvergira u tiipu konvergencije A da to mora biti prema istoj funkciji onda je jasno da ako konvergira u tiipu konvergencije A da to mora biti prema istoj funkciji  . Naime, ukoliko bi u tipu konvergencije A konvergirao prema nekoj drugoj funkciji . Naime, ukoliko bi u tipu konvergencije A konvergirao prema nekoj drugoj funkciji  , onda, pošto tip konvergencije A povlači tip konvergencije B, dobivamo da i u tipu konvergencije B konvergira prema , onda, pošto tip konvergencije A povlači tip konvergencije B, dobivamo da i u tipu konvergencije B konvergira prema  , a to je kontradikcija s tim da u tipu konvergencije B konvergira prema , a to je kontradikcija s tim da u tipu konvergencije B konvergira prema  . .
Dakle, kod provjeravanja bilo kojeg od 5 tipova konvergencije, ako pokažeš da u jednom od njih konvergira prema  onda znaš da u svima ostalima, ako u njima konvergira, mora konvergirati prema istom tom onda znaš da u svima ostalima, ako u njima konvergira, mora konvergirati prema istom tom  . .
| Zvjezdica (napisa): | E i još kod ove provjere po točkama, ako vidimo da je 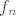 oblika 1/nešto, možemo zaključiti da konvergira prema 0 za oblika 1/nešto, možemo zaključiti da konvergira prema 0 za 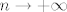 i ne trebamo dalje provjeravati? i ne trebamo dalje provjeravati? |
Rekao bih da da, naravno, moraš paziti da to nešto ovisi o  i da to nešto teži u ful puno kako i da to nešto teži u ful puno kako  teži u ful puno i to za svaki fiksni teži u ful puno i to za svaki fiksni  iz domene. Normalno, to u slučaju da provjeravaš točkovnu konvergenciju. iz domene. Normalno, to u slučaju da provjeravaš točkovnu konvergenciju.
| Zvjezdica (napisa): | Kod primjera
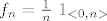
napisali smo za konvergenciju po mjeri
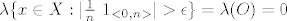
Zašto prazan skup a ne 1? mislim opet ispada  |
Pretpostavljam da ti nedostaje limes, evo, napisati ću sve lijepo! 
Neka je  , za svaki , za svaki  definirajmo definirajmo
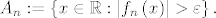
Opet koristimo Arhimedov akisom prema kojem znamo da postoji dovoljno velik  takav da je takav da je  . Dakle, za svaki . Dakle, za svaki 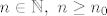 je je 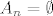 . Konačno, za svaki . Konačno, za svaki  dobivamo da je dobivamo da je
 . .
Eto ga, nadam se da je sve razjašnjeno! 
|
|
| [Vrh] |
|
Zvjezdica
Forumaš(ica)

Pridružen/a: 02. 07. 2009. (12:40:02)
Postovi: (58)16
|
|
| [Vrh] |
|
|












