| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 14:39 sub, 11. 6. 2011 Naslov: Postano: 14:39 sub, 11. 6. 2011 Naslov: |
    |
|
|
Što se radi u njemu? Pa, ova jako komplicirana funkcija je napravljena tako da ''legne'' u Rolleov teorem - tj. da se primjenom Rolleovog teorema dobije rezultat.
Taylorov teorem se prilično koristi kasnije kod Taylorovih redova, a također i u ovom poglavlju o derivacijama (teorem odmah poslije).
E sad, mislim da je najveći problem u dokazu zapravo zapamtiti ovu jako kompliciranu funkciju. :) Pa ću probati to malo olakšati.
Pogledaj malo iznad tog teorema definiciju Taylorovog polinoma i n-tog ostatka Taylorovog polinoma.
Znam da se u skripti tako ne označava, ali kod Taylorovog polinoma je bitno više stvari, zato je [latex]T_n(x)[/latex] malo nespretna oznaka za njega. Također je bitno i u kojoj točki je Taylorov polinom, tako da ću označiti
[latex]T_n(x, c)[/latex] Taylorov polinom n-tog reda funkcije f oko točke c.
Kad tako gledaš onda u dokazu možeš ovo F(t) napisati kao:
[latex]F(t) = f(x) - T_n(x, t) - A \frac {(x-t)^{n+1}} {(n+1)!} [/latex], gdje je [latex]A = \frac {(n+1)!} {(x-c)^{n+1}} (f(x) - T_n(x, c)) [/latex]
Ako hoćeš još kompaktnije to zapisati, možeš primijeniti da je f(x) - Tn zapravo taj ostatak Rn...
Pa bi mogao pisati [latex]f(x) - T_n(x, t) = R_n(x, t)[/latex]
Mislim da je ovako jednostavnije i vidjeti zašto je F(c) = 0.
[latex]F(c) = f(x) - T_n(x, c) - (f(x) - T_n(x, c)) = 0[/latex]
Znam da nije neka jako velika pomoć, ali bar je nekako jednostavnije za zapamtiti (naravno, kad znaš formulu za Tn i Rn).
Mislim da trebaš još to malo bolje raspisati, jer je u skripti dosta koraka preskočeno. Ako ti još nešto nije jasno ili bi htio da neke korake detaljnije objasnim, samo pitaj.
Što se radi u njemu? Pa, ova jako komplicirana funkcija je napravljena tako da ''legne'' u Rolleov teorem - tj. da se primjenom Rolleovog teorema dobije rezultat.
Taylorov teorem se prilično koristi kasnije kod Taylorovih redova, a također i u ovom poglavlju o derivacijama (teorem odmah poslije).
E sad, mislim da je najveći problem u dokazu zapravo zapamtiti ovu jako kompliciranu funkciju.  Pa ću probati to malo olakšati. Pa ću probati to malo olakšati.
Pogledaj malo iznad tog teorema definiciju Taylorovog polinoma i n-tog ostatka Taylorovog polinoma.
Znam da se u skripti tako ne označava, ali kod Taylorovog polinoma je bitno više stvari, zato je 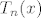 malo nespretna oznaka za njega. Također je bitno i u kojoj točki je Taylorov polinom, tako da ću označiti malo nespretna oznaka za njega. Također je bitno i u kojoj točki je Taylorov polinom, tako da ću označiti
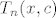 Taylorov polinom n-tog reda funkcije f oko točke c. Taylorov polinom n-tog reda funkcije f oko točke c.
Kad tako gledaš onda u dokazu možeš ovo F(t) napisati kao:
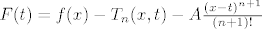 , gdje je , gdje je 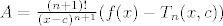
Ako hoćeš još kompaktnije to zapisati, možeš primijeniti da je f(x) - Tn zapravo taj ostatak Rn...
Pa bi mogao pisati 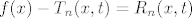
Mislim da je ovako jednostavnije i vidjeti zašto je F(c) = 0.
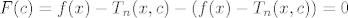
Znam da nije neka jako velika pomoć, ali bar je nekako jednostavnije za zapamtiti (naravno, kad znaš formulu za Tn i Rn).
Mislim da trebaš još to malo bolje raspisati, jer je u skripti dosta koraka preskočeno. Ako ti još nešto nije jasno ili bi htio da neke korake detaljnije objasnim, samo pitaj.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 11:18 pon, 13. 6. 2011 Naslov: Postano: 11:18 pon, 13. 6. 2011 Naslov: |
    |
|
|
U prvom dijelu tog teorema se kaže da kod redova sa pozitivnim članovima vrijedi [latex]\sum a_n = sup\{s_n | n \in N\}[/latex]. U dokazu se želi pokazati da vrijedi [latex]sup\{s_n | n \in N\} \leq sup\{s'_m | m \in N\} [/latex] i [latex]sup\{s_n | n \in N\} \geq sup\{s'_m | m \in N\} [/latex] iz čega će slijediti da su ta dva supremuma jednaka iz čega će slijediti da su te dvije sume jednake.
(Označavat ću sa a', s', elemente ovog drugog, permutiranog reda, tako je i u skripti. Koristit ću i druge oznake iz skripte, ovaj sigma i to).
E sad, pokazat ću samo jedan smjer, možda ti je malo zbunjujuće što su u skripti obadva izvedena paralelno.
Znači, prvi korak - za bilo koji [latex]n \in N[/latex] postoji [latex]p \in N[/latex] tako da je [latex]\sigma(1) < p, ..., \sigma (n) < p[/latex].
Ako razumiješ što je permutacija, mislim da bi ovo trebalo biti prilično jasno, al samo pitaj ako nije.
I odatle - vidi u skripti - [latex]s'_n \leq s_p[/latex], baš zbog takvog izbora p i zato jer red ima pozitivne članove - pa iz toga slijedi ovo manje-ili-jednako kod odgovarajućih supremuma. Opet pitaj ako ti što treba pojasniti oko ovoga.
(Znam da nisam baš previše objašnjavao, al mi je lakše kad ti upreš prstom na dio koji ti nije jasan... Nejasnoća je vjerojatno oko jednog od ova dva koraka :) )
U prvom dijelu tog teorema se kaže da kod redova sa pozitivnim članovima vrijedi 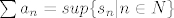 . U dokazu se želi pokazati da vrijedi . U dokazu se želi pokazati da vrijedi 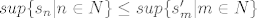 i i 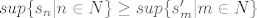 iz čega će slijediti da su ta dva supremuma jednaka iz čega će slijediti da su te dvije sume jednake. iz čega će slijediti da su ta dva supremuma jednaka iz čega će slijediti da su te dvije sume jednake.
(Označavat ću sa a', s', elemente ovog drugog, permutiranog reda, tako je i u skripti. Koristit ću i druge oznake iz skripte, ovaj sigma i to).
E sad, pokazat ću samo jedan smjer, možda ti je malo zbunjujuće što su u skripti obadva izvedena paralelno.
Znači, prvi korak - za bilo koji 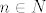 postoji postoji 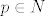 tako da je tako da je 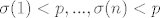 . .
Ako razumiješ što je permutacija, mislim da bi ovo trebalo biti prilično jasno, al samo pitaj ako nije.
I odatle - vidi u skripti - 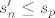 , baš zbog takvog izbora p i zato jer red ima pozitivne članove - pa iz toga slijedi ovo manje-ili-jednako kod odgovarajućih supremuma. Opet pitaj ako ti što treba pojasniti oko ovoga. , baš zbog takvog izbora p i zato jer red ima pozitivne članove - pa iz toga slijedi ovo manje-ili-jednako kod odgovarajućih supremuma. Opet pitaj ako ti što treba pojasniti oko ovoga.
(Znam da nisam baš previše objašnjavao, al mi je lakše kad ti upreš prstom na dio koji ti nije jasan... Nejasnoća je vjerojatno oko jednog od ova dva koraka  ) )
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 12:13 pon, 13. 6. 2011 Naslov: Postano: 12:13 pon, 13. 6. 2011 Naslov: |
    |
|
|
Ja ću to seljački probati objasniti.
Jedan red je a1 + a2 + a3 + a4... koji konvergira.
Drugi red je permutacija: a3 + a8 + a4 + a7 + ... za koji dokazuješ da konvergira također.
Ideja je ova: bilo koja parcijalna suma tog "permutiranog" reda, recimo a3 + a8 + a4 + a7, manja je od neke parcijalne sume prvotnog reda, ovdje konkretno od a1 + ... + a9. Nadam se da je jasno zašto.
Ista argumentacija vrijedi i obrnuto: označimo li članove našeg permutiranog reda a3 + a8 + a4 + a7 + ..., kao b1 + b2 + b3 + b4 + ..., onda je prvotni red zapravo neka permutacija b-ova.
Ja ću to seljački probati objasniti.
Jedan red je a1 + a2 + a3 + a4... koji konvergira.
Drugi red je permutacija: a3 + a8 + a4 + a7 + ... za koji dokazuješ da konvergira također.
Ideja je ova: bilo koja parcijalna suma tog "permutiranog" reda, recimo a3 + a8 + a4 + a7, manja je od neke parcijalne sume prvotnog reda, ovdje konkretno od a1 + ... + a9. Nadam se da je jasno zašto.
Ista argumentacija vrijedi i obrnuto: označimo li članove našeg permutiranog reda a3 + a8 + a4 + a7 + ..., kao b1 + b2 + b3 + b4 + ..., onda je prvotni red zapravo neka permutacija b-ova.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
|






