| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 11:00 sri, 7. 9. 2011 Naslov: Postano: 11:00 sri, 7. 9. 2011 Naslov: |
    |
|
|
Konkavna. Naime, dana je [u]kvadratna funkcija[/u] po varijabli a. Neka te ne buni ovo x. To je nekakav parametar, ali on u ovom slučaju nikako ne utječe na konveksnost/konkavnost funkcije. Promatraš vodeći koeficijent (odnosno, koeficijent uz najveću potenciju varijable). On je jednak -1. Znamo da ako je taj koeficijent pozitivan, "otvor" kvadratne funkcije je otvoren prema gore (konveksna je; tangenta se nalazi "ispod" funkcije za svaki izbor varijable a); a ako je vodeći koeficijent negativan, "otvor" kvadratne funkcije je okrenut prema dolje (konkavna je; tangenta se nalazi "iznad" funkcije za svaki izbor varijable a).
p.s. Da nije možda f(x), a ne f(a)?
Konkavna. Naime, dana je kvadratna funkcija po varijabli a. Neka te ne buni ovo x. To je nekakav parametar, ali on u ovom slučaju nikako ne utječe na konveksnost/konkavnost funkcije. Promatraš vodeći koeficijent (odnosno, koeficijent uz najveću potenciju varijable). On je jednak -1. Znamo da ako je taj koeficijent pozitivan, "otvor" kvadratne funkcije je otvoren prema gore (konveksna je; tangenta se nalazi "ispod" funkcije za svaki izbor varijable a); a ako je vodeći koeficijent negativan, "otvor" kvadratne funkcije je okrenut prema dolje (konkavna je; tangenta se nalazi "iznad" funkcije za svaki izbor varijable a).
p.s. Da nije možda f(x), a ne f(a)?
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 9:55 čet, 8. 9. 2011 Naslov: Postano: 9:55 čet, 8. 9. 2011 Naslov: |
    |
|
|
U slučaju kako si ti napisao, oba su korijena u tom intervalu. Tebe zanimaju dvije situacije:
1) [latex]f(0)>0; f(2)< 0[/latex]
2) [latex]f(0)< 0; f(2) >0[/latex]
Dakle, na tom intervalu funkcija mijenja predznak, zato imamo ta dva slučaja.
Da je ovako kako si ti napisao, bile bi dvije mogućnosti:
1) na intervalu [latex]<0, 2>[/latex] ima dva korijena ili jedan dvostruki (što je zapravo opet [u]dva[/u] rješenja, ali se ona preklapaju)
2) funkcija nema realnih korijena, odnosno diskriminanta je negativna, pa je cijela "iznad" x-osi
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
Nego, da se vratim kratko na onaj prethodni zadatak kada se traži da jednadžba ima jedno negativno rješenje.
Unaprijed ću se ograditi od ovog rješenja jer zadatak nije potpuno postavljen. Da li zadatak traži da jednadžba ima jedno negativno, a jedno pozitivno rješenje ili da jednadžba ima točno jedno rješenje koje je negativno? Ja rješavam za ovu prvu interpretaciju koju sam napisao iz jednostavnog razloga jer kvadratna jednadžba UVIJEK ima dva rješenja, samo se u nekim situacijama ta dva rješenja poklapaju, pa bi u slučaju da se rješava po drugoj interpretaciji bilo točnije napisati "kad jednadžba ima jedno [u]dvostruko[/u] negativno rješenje?".
Neka funkcija [latex]f(x)[/latex] ima dva korijena: [latex]x_1 > 0, x_2<0[/latex]. Koliki je onda umnožak tih dvaju rješenja? [latex]x_1x_2 < 0[/latex]. Po Vieteovim formulama znamo da je [latex]x_1x_2 = \frac{c}{a}[/latex]. Odnosno, uvijet je [tex]\frac{c}{a}<0[/tex], tj. [tex]\frac{m-3}{2m+1}<0[/tex], što se lako riješi.
Kad fja ima dva negativna rješenja? Kad je umnožak [tex]x_1x_2>0[/tex]. Naravno, ovdje sad imamo situaciju da ćemo dobiti više rješenja negoli je potrebno jer će umnožak biti pozitivan i ako su oba korijena pozitivna. Sjetimo se i da znamo Vieteovu formulu za zbroj korijena, pa i to primijenimo. Zbroj dva negativna korijena će biti negativan, pa dodatno imamo i [tex]x_1+x_2 < 0[/tex]. Riješimo taj sustav i dobijemo rješenje.
U slučaju kako si ti napisao, oba su korijena u tom intervalu. Tebe zanimaju dvije situacije:
1) 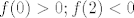
2) 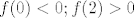
Dakle, na tom intervalu funkcija mijenja predznak, zato imamo ta dva slučaja.
Da je ovako kako si ti napisao, bile bi dvije mogućnosti:
1) na intervalu 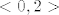 ima dva korijena ili jedan dvostruki (što je zapravo opet dva rješenja, ali se ona preklapaju) ima dva korijena ili jedan dvostruki (što je zapravo opet dva rješenja, ali se ona preklapaju)
2) funkcija nema realnih korijena, odnosno diskriminanta je negativna, pa je cijela "iznad" x-osi
Added after 11 minutes:
Nego, da se vratim kratko na onaj prethodni zadatak kada se traži da jednadžba ima jedno negativno rješenje.
Unaprijed ću se ograditi od ovog rješenja jer zadatak nije potpuno postavljen. Da li zadatak traži da jednadžba ima jedno negativno, a jedno pozitivno rješenje ili da jednadžba ima točno jedno rješenje koje je negativno? Ja rješavam za ovu prvu interpretaciju koju sam napisao iz jednostavnog razloga jer kvadratna jednadžba UVIJEK ima dva rješenja, samo se u nekim situacijama ta dva rješenja poklapaju, pa bi u slučaju da se rješava po drugoj interpretaciji bilo točnije napisati "kad jednadžba ima jedno dvostruko negativno rješenje?".
Neka funkcija 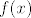 ima dva korijena: ima dva korijena: 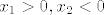 . Koliki je onda umnožak tih dvaju rješenja? . Koliki je onda umnožak tih dvaju rješenja? 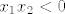 . Po Vieteovim formulama znamo da je . Po Vieteovim formulama znamo da je 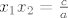 . Odnosno, uvijet je [tex]\frac{c}{a}<0[/tex], tj. [tex]\frac{m-3}{2m+1}<0[/tex], što se lako riješi. . Odnosno, uvijet je [tex]\frac{c}{a}<0[/tex], tj. [tex]\frac{m-3}{2m+1}<0[/tex], što se lako riješi.
Kad fja ima dva negativna rješenja? Kad je umnožak [tex]x_1x_2>0[/tex]. Naravno, ovdje sad imamo situaciju da ćemo dobiti više rješenja negoli je potrebno jer će umnožak biti pozitivan i ako su oba korijena pozitivna. Sjetimo se i da znamo Vieteovu formulu za zbroj korijena, pa i to primijenimo. Zbroj dva negativna korijena će biti negativan, pa dodatno imamo i [tex]x_1+x_2 < 0[/tex]. Riješimo taj sustav i dobijemo rješenje.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 15:39 čet, 8. 9. 2011 Naslov: Postano: 15:39 čet, 8. 9. 2011 Naslov: |
    |
|
|
Da, dobro je, [tex]m \in <0, 4>[/tex]. S tim da ovaj drugi slučaj nisi ni trebao provesti do kraja. Čim si vidio uvjet [tex]m^2<0[/tex] znaš da je taj slučaj nemoguć.
Nego, jesi shvatio zašto se zadatak postavlja da je [tex]f(0)>0, f(2)<0[/tex]?
Da, dobro je, [tex]m \in <0, 4>[/tex]. S tim da ovaj drugi slučaj nisi ni trebao provesti do kraja. Čim si vidio uvjet [tex]m^2<0[/tex] znaš da je taj slučaj nemoguć.
Nego, jesi shvatio zašto se zadatak postavlja da je [tex]f(0)>0, f(2)<0[/tex]?
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 22:45 čet, 8. 9. 2011 Naslov: Postano: 22:45 čet, 8. 9. 2011 Naslov: |
    |
|
|
Ok, onda ajmo to još srediti. Dakle, kvadratna je funkcija neprekidna funkcija. To nam je bitno zbog konačnog zaključka. Nacrtaj si interval [tex]<0, 2>[/tex]. U [tex]x = 0[/tex] stavi da je [tex]y >0[/tex] - to nam je zbog [tex]f(0)>0[/tex]; a u [tex]x = 2[/tex] stavi da je [tex]y < 0[/tex] - to nam je zbog [tex]f(2)<0[/tex]. Slikovito rečeno, za [tex]x = 0[/tex] funkcija vrijednost će biti iznad osi x, a za [tex]x = 2[/tex] funkcija će vrijednost biti ispod osi x. E sad, povuci liniju između te dvije točke. Koliko će puta ta linija presjeći os x? SAMO JEDNOM. Dakle, na tom će intervali imati samo jednu nultočku.
Jasnije?
Ok, onda ajmo to još srediti. Dakle, kvadratna je funkcija neprekidna funkcija. To nam je bitno zbog konačnog zaključka. Nacrtaj si interval [tex]<0, 2>[/tex]. U [tex]x = 0[/tex] stavi da je [tex]y >0[/tex] - to nam je zbog [tex]f(0)>0[/tex]; a u [tex]x = 2[/tex] stavi da je [tex]y < 0[/tex] - to nam je zbog [tex]f(2)<0[/tex]. Slikovito rečeno, za [tex]x = 0[/tex] funkcija vrijednost će biti iznad osi x, a za [tex]x = 2[/tex] funkcija će vrijednost biti ispod osi x. E sad, povuci liniju između te dvije točke. Koliko će puta ta linija presjeći os x? SAMO JEDNOM. Dakle, na tom će intervali imati samo jednu nultočku.
Jasnije?
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
|









