| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
 Postano: 20:13 pon, 24. 10. 2011 Naslov: Postano: 20:13 pon, 24. 10. 2011 Naslov: |
    |
|
|
Pretpostavljam da je ovo 09_10 viška u adresi, jer mi link radi samo bez toga.
2. zadatak:
Kakvi su to polinomi koji su jednaki u x i u -x, i to za svako x? To znači da su simetrični s obzirom na y-os? A, koji su polinomi jedini koji to zadovoljavaju?
Ako uzmemo proizvoljan polinom n-tog stupnja i gledamo f(x) i f(-x), vidimo da nam članovi parnog stupnja ne prave problem, dok ovi drugi... da. Pošto smo uzeli proizvoljan x, dakle bilo koji, a prebacivanjem u oblik f(x) - f(-x) = 0 dobijemo nekakav polinom u kojem će uz sve neparne stupnjeve stajati dvostruki koeficijenti, a s desne strane nulpolinom, pa slijedi da svi oni moraju biti nula.
Dakle, lako se pokaže da su to polinomi koji u sebi sadrže samo članove parnog stupnja (uključujući i nultog i uključujući i nulpolinom, naravno), a od tamo je očita i jedna baza: {[latex]1, x^2, x^4,[/latex] ..... do [latex] x^n[/latex] ili do [latex] x^{n-1}[/latex]}, i baza komplementa: {[latex]x, x^3, x^5[/latex], ... i isti komentar kao i gore}, i dimenzija (najveće cijelo od n/2). Ako treba još, raspisat ću i više.
3.a)
Pošto su uvjeti, tako reći, linearni :P, naslućujemo da zaista i je potprostor. I da, sad to treba raspisivanjem i pokazati, ako uzmemo proizvoljna dva elementa iz tog skupa
[latex]a = (a_1 + a_2 i, -a_2 + a_1 i, -a_1 - a_2 i)[/latex]
i
[latex]b = (b_1 + b_2 i, -b_2 + b_1 i, -b_1 - b_2 i)[/latex]
lako se pokaže da je njihov zbroj i dalje u tom skupu. Dakle, dosta je pokazati da je [latex]\alpha a[/latex] i dalje iz tog skupa. Jedino se postavlja pitanje: odakle je [latex]\alpha[/latex] ? Ako je realan, onda je to trivijalno za pokazati. Ako nije... onda ima ipak malo više raspisivane, no da se :P
Drugi način je da se primjeti da je a zapravo oblika:
[latex]a = (x_1, i*x_1, -x_1) [/latex], gdje je x_1 kompleksan, i ovo nam čini raspisivanje puno ugodnijim. :P
3. b)
Uvjet "nešto NIJE jednako nečemu" je jako... neobičan. To bi trebao biti prvi hint da ovo nije potprostor, dakle tražimo protuprimjer. Najtrivijalni protuprimjer jest taj da nulvektor nije element tog skupa jer je 0+0 = 0, a nulvektor nam je potrebno da bi uopće bio vektorski prostor, a kamo li tek potprostor!
Nekim drugim naštimavanjima bi se isto to moglo pokazati, no ovo je najtrivijalniji, a jako čest, protuprimjer.
Pretpostavljam da je ovo 09_10 viška u adresi, jer mi link radi samo bez toga.
2. zadatak:
Kakvi su to polinomi koji su jednaki u x i u -x, i to za svako x? To znači da su simetrični s obzirom na y-os? A, koji su polinomi jedini koji to zadovoljavaju?
Ako uzmemo proizvoljan polinom n-tog stupnja i gledamo f(x) i f(-x), vidimo da nam članovi parnog stupnja ne prave problem, dok ovi drugi... da. Pošto smo uzeli proizvoljan x, dakle bilo koji, a prebacivanjem u oblik f(x) - f(-x) = 0 dobijemo nekakav polinom u kojem će uz sve neparne stupnjeve stajati dvostruki koeficijenti, a s desne strane nulpolinom, pa slijedi da svi oni moraju biti nula.
Dakle, lako se pokaže da su to polinomi koji u sebi sadrže samo članove parnog stupnja (uključujući i nultog i uključujući i nulpolinom, naravno), a od tamo je očita i jedna baza: {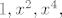 ..... do ..... do 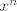 ili do ili do 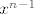 }, i baza komplementa: { }, i baza komplementa: {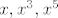 , ... i isti komentar kao i gore}, i dimenzija (najveće cijelo od n/2). Ako treba još, raspisat ću i više. , ... i isti komentar kao i gore}, i dimenzija (najveće cijelo od n/2). Ako treba još, raspisat ću i više.
3.a)
Pošto su uvjeti, tako reći, linearni  , naslućujemo da zaista i je potprostor. I da, sad to treba raspisivanjem i pokazati, ako uzmemo proizvoljna dva elementa iz tog skupa , naslućujemo da zaista i je potprostor. I da, sad to treba raspisivanjem i pokazati, ako uzmemo proizvoljna dva elementa iz tog skupa
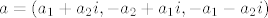
i
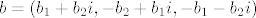
lako se pokaže da je njihov zbroj i dalje u tom skupu. Dakle, dosta je pokazati da je 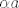 i dalje iz tog skupa. Jedino se postavlja pitanje: odakle je i dalje iz tog skupa. Jedino se postavlja pitanje: odakle je  ? Ako je realan, onda je to trivijalno za pokazati. Ako nije... onda ima ipak malo više raspisivane, no da se ? Ako je realan, onda je to trivijalno za pokazati. Ako nije... onda ima ipak malo više raspisivane, no da se 
Drugi način je da se primjeti da je a zapravo oblika:
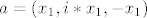 , gdje je x_1 kompleksan, i ovo nam čini raspisivanje puno ugodnijim. , gdje je x_1 kompleksan, i ovo nam čini raspisivanje puno ugodnijim. 
3. b)
Uvjet "nešto NIJE jednako nečemu" je jako... neobičan. To bi trebao biti prvi hint da ovo nije potprostor, dakle tražimo protuprimjer. Najtrivijalni protuprimjer jest taj da nulvektor nije element tog skupa jer je 0+0 = 0, a nulvektor nam je potrebno da bi uopće bio vektorski prostor, a kamo li tek potprostor!
Nekim drugim naštimavanjima bi se isto to moglo pokazati, no ovo je najtrivijalniji, a jako čest, protuprimjer.
_________________
Ceterum censeo Carthaginem esse delendam.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 21:11 pet, 28. 10. 2011 Naslov: Postano: 21:11 pet, 28. 10. 2011 Naslov: |
    |
|
|
i može zadatak 4 neko pokazati ovo s linearnom ljuskom??
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
[quote="Borgcube"]Pretpostavljam da je ovo 09_10 viška u adresi, jer mi link radi samo bez toga.
2. zadatak:
Kakvi su to polinomi koji su jednaki u x i u -x, i to za svako x? To znači da su simetrični s obzirom na y-os? A, koji su polinomi jedini koji to zadovoljavaju?
Ako uzmemo proizvoljan polinom n-tog stupnja i gledamo f(x) i f(-x), vidimo da nam članovi parnog stupnja ne prave problem, dok ovi drugi... da. Pošto smo uzeli proizvoljan x, dakle bilo koji, a prebacivanjem u oblik f(x) - f(-x) = 0 dobijemo nekakav polinom u kojem će uz sve neparne stupnjeve stajati dvostruki koeficijenti, a s desne strane nulpolinom, pa slijedi da svi oni moraju biti nula.
Dakle, lako se pokaže da su to polinomi koji u sebi sadrže samo članove parnog stupnja (uključujući i nultog i uključujući i nulpolinom, naravno), a od tamo je očita i jedna baza: {[latex]1, x^2, x^4,[/latex] ..... do [latex] x^n[/latex] ili do [latex] x^{n-1}[/latex]}, i baza komplementa: {[latex]x, x^3, x^5[/latex], ... i isti komentar kao i gore}, i dimenzija (najveće cijelo od n/2).[b] [size=18]Ako treba još, raspisat ću i više.[/size][/b]
3.a)
Pošto su uvjeti, tako reći, linearni :P, naslućujemo da zaista i je potprostor. I da, sad to treba raspisivanjem i pokazati, ako uzmemo proizvoljna dva elementa iz tog skupa
[latex]a = (a_1 + a_2 i, -a_2 + a_1 i, -a_1 - a_2 i)[/latex]
i
[latex]b = (b_1 + b_2 i, -b_2 + b_1 i, -b_1 - b_2 i)[/latex]
lako se pokaže da je njihov zbroj i dalje u tom skupu. Dakle, dosta je pokazati da je [latex]\alpha a[/latex] i dalje iz tog skupa. Jedino se postavlja pitanje: odakle je [latex]\alpha[/latex] ? Ako je realan, onda je to trivijalno za pokazati. Ako nije... onda ima ipak malo više raspisivane, no da se :P
Drugi način je da se primjeti da je a zapravo oblika:
[latex]a = (x_1, i*x_1, -x_1) [/latex], gdje je x_1 kompleksan, i ovo nam čini raspisivanje puno ugodnijim. :P
3. b)
Uvjet "nešto NIJE jednako nečemu" je jako... neobičan. To bi trebao biti prvi hint da ovo nije potprostor, dakle tražimo protuprimjer. Najtrivijalni protuprimjer jest taj da nulvektor nije element tog skupa jer je 0+0 = 0, a nulvektor nam je potrebno da bi uopće bio vektorski prostor, a kamo li tek potprostor!
Nekim drugim naštimavanjima bi se isto to moglo poazati, no ovo je najtrivijalniji, a jako čest, protuprimjer.[/quote]
može :D
i može zadatak 4 neko pokazati ovo s linearnom ljuskom??
Added after 12 minutes:
| Borgcube (napisa): | Pretpostavljam da je ovo 09_10 viška u adresi, jer mi link radi samo bez toga.
2. zadatak:
Kakvi su to polinomi koji su jednaki u x i u -x, i to za svako x? To znači da su simetrični s obzirom na y-os? A, koji su polinomi jedini koji to zadovoljavaju?
Ako uzmemo proizvoljan polinom n-tog stupnja i gledamo f(x) i f(-x), vidimo da nam članovi parnog stupnja ne prave problem, dok ovi drugi... da. Pošto smo uzeli proizvoljan x, dakle bilo koji, a prebacivanjem u oblik f(x) - f(-x) = 0 dobijemo nekakav polinom u kojem će uz sve neparne stupnjeve stajati dvostruki koeficijenti, a s desne strane nulpolinom, pa slijedi da svi oni moraju biti nula.
Dakle, lako se pokaže da su to polinomi koji u sebi sadrže samo članove parnog stupnja (uključujući i nultog i uključujući i nulpolinom, naravno), a od tamo je očita i jedna baza: {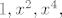 ..... do ..... do 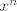 ili do ili do 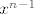 }, i baza komplementa: { }, i baza komplementa: {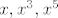 , ... i isti komentar kao i gore}, i dimenzija (najveće cijelo od n/2). Ako treba još, raspisat ću i više. , ... i isti komentar kao i gore}, i dimenzija (najveće cijelo od n/2). Ako treba još, raspisat ću i više.
3.a)
Pošto su uvjeti, tako reći, linearni  , naslućujemo da zaista i je potprostor. I da, sad to treba raspisivanjem i pokazati, ako uzmemo proizvoljna dva elementa iz tog skupa , naslućujemo da zaista i je potprostor. I da, sad to treba raspisivanjem i pokazati, ako uzmemo proizvoljna dva elementa iz tog skupa
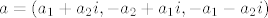
i
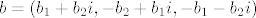
lako se pokaže da je njihov zbroj i dalje u tom skupu. Dakle, dosta je pokazati da je 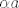 i dalje iz tog skupa. Jedino se postavlja pitanje: odakle je i dalje iz tog skupa. Jedino se postavlja pitanje: odakle je  ? Ako je realan, onda je to trivijalno za pokazati. Ako nije... onda ima ipak malo više raspisivane, no da se ? Ako je realan, onda je to trivijalno za pokazati. Ako nije... onda ima ipak malo više raspisivane, no da se 
Drugi način je da se primjeti da je a zapravo oblika:
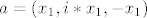 , gdje je x_1 kompleksan, i ovo nam čini raspisivanje puno ugodnijim. , gdje je x_1 kompleksan, i ovo nam čini raspisivanje puno ugodnijim. 
3. b)
Uvjet "nešto NIJE jednako nečemu" je jako... neobičan. To bi trebao biti prvi hint da ovo nije potprostor, dakle tražimo protuprimjer. Najtrivijalni protuprimjer jest taj da nulvektor nije element tog skupa jer je 0+0 = 0, a nulvektor nam je potrebno da bi uopće bio vektorski prostor, a kamo li tek potprostor!
Nekim drugim naštimavanjima bi se isto to moglo poazati, no ovo je najtrivijalniji, a jako čest, protuprimjer. |
može 
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
 Postano: 20:48 ned, 30. 10. 2011 Naslov: Postano: 20:48 ned, 30. 10. 2011 Naslov: |
    |
|
|
Pretpostavit ću da se raspis odnosi samo na 2. zadatak. :P
Dakle, znamo da je potprostor i sad trebamo otkriti kakav je. Pa, idemo prvo provjeriti što nam to kaže uvjet, uzmemo f(x) općeniti polinom n-tog stupnja koji živi u tom skupu, dakle vrijedi:
[latex]f(x) = a_0+a_1x+a_2x^2+...+a_nx^n[/latex]
i gledamo f(x) = f(-x), tj.:
[latex]f(x) = a_0+a_1x+a_2x^2+a_3x^3+a_4x^4...+a_nx^n=f(-x)=a_0-a_1x+a_2x^2-a_3x^3+a_4x^4+....\pma_nx^n - (ovisno o parnosti od n)[/latex]
Sada prebacivanjem dobijemo
[latex]f(x)-f(-x) = 0[/latex]
tj.
[latex]f(x)-f(-x) = 2a_1x+2a_3x^3+2a_5x^5...=0[/latex]
- zadnji član ovisi o parnosti od n, jer očito će svaka parna potencija poništiti samu sebe, a svaka neparna će se udvostručiti.
No, ovo je zapravo jednakost nekog polinoma sa nulpolinomom, pa po teoremu o nulpolinomu slijedi:
[latex]2a_1=2a_3=2a_5=...=0[/latex]
tj.
[latex]a_1=a_3=a_5=...=0[/latex]
Dakle, f(x) uopće ne sadrži članove uz koje stoji [latex]x^{neparna potencija}[/latex] (koeficijenti uz te članove su 0), a kako na uvjet uopće ne utječu članovi sa parnom potencijom, slijedi da je f(x) je linearna kombinacija članova skupa:
[latex]A =\{1,x^2,x^4,x^6,....x^{n-1} ili x^n\}[/latex] - zadnji član, naravno, ovisi o tome je li n paran ili nije. Ako je, onda je [latex]x^n[/latex] unutra, ako nije onda je [latex]x^{n-1}[/latex].
Vidimo da je A sustav izvodnica za zadan potprostor, a kako je A podskup kanonske baze, dakle podskup linearno nezavisnog skupa, slijedi da je i A linearno nezavisan skup. Dakle, A je baza za zadani potprostor.
Preostaje odrediti koliko se članova nalazi u A. Za n paran baza cijelog prostora sadrži n+1 članova, a skup A sadrži n/2+1, dok za n neparan A sadrži n/2+1/2.
Oba slučaja se mogu obuhvatiti sa
[latex]\lceil {n+1}/2 \rceil[/latex], i čini mi se da sam to krivo napisao u gornjem postu :oops: , no taj detalj je i tako nevažan, dosta je raspisati ovo gore.
3. a) je, ako se upotrijebi štos koji sam napisao, jako lagano raspisivanje koje ste morali vidjeti već puno puta na vježbama i nema ništa posebno pametno u njemu.
3. b) se svodi na to da vidimo da nulvektor ne zadovoljava
[latex]x+z\neqy[/latex], a svaki potprostor mora sadržavati nulvektor dakle kraj.
Ako postoji 1 protuprimjer, postoji ih beskonačno, ideja je da prepoznate da uvjet
[latex]x+z\neqy[/latex]
NIJE linearan, dakle ovo nije potprostor, i onda počnete tražiti protuprimjer ili, alternativno, počnete dokazivati da je i zapnete pa se onda zapitate je li stvarno.
Pretpostavit ću da se raspis odnosi samo na 2. zadatak. 
Dakle, znamo da je potprostor i sad trebamo otkriti kakav je. Pa, idemo prvo provjeriti što nam to kaže uvjet, uzmemo f(x) općeniti polinom n-tog stupnja koji živi u tom skupu, dakle vrijedi:
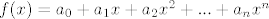
i gledamo f(x) = f(-x), tj.:
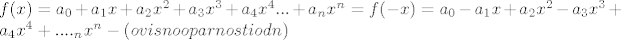
Sada prebacivanjem dobijemo
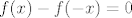
tj.
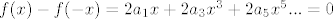
- zadnji član ovisi o parnosti od n, jer očito će svaka parna potencija poništiti samu sebe, a svaka neparna će se udvostručiti.
No, ovo je zapravo jednakost nekog polinoma sa nulpolinomom, pa po teoremu o nulpolinomu slijedi:
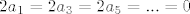
tj.
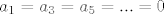
Dakle, f(x) uopće ne sadrži članove uz koje stoji 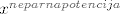 (koeficijenti uz te članove su 0), a kako na uvjet uopće ne utječu članovi sa parnom potencijom, slijedi da je f(x) je linearna kombinacija članova skupa: (koeficijenti uz te članove su 0), a kako na uvjet uopće ne utječu članovi sa parnom potencijom, slijedi da je f(x) je linearna kombinacija članova skupa:
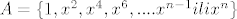 - zadnji član, naravno, ovisi o tome je li n paran ili nije. Ako je, onda je - zadnji član, naravno, ovisi o tome je li n paran ili nije. Ako je, onda je 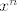 unutra, ako nije onda je unutra, ako nije onda je 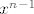 . .
Vidimo da je A sustav izvodnica za zadan potprostor, a kako je A podskup kanonske baze, dakle podskup linearno nezavisnog skupa, slijedi da je i A linearno nezavisan skup. Dakle, A je baza za zadani potprostor.
Preostaje odrediti koliko se članova nalazi u A. Za n paran baza cijelog prostora sadrži n+1 članova, a skup A sadrži n/2+1, dok za n neparan A sadrži n/2+1/2.
Oba slučaja se mogu obuhvatiti sa
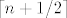 , i čini mi se da sam to krivo napisao u gornjem postu , i čini mi se da sam to krivo napisao u gornjem postu  , no taj detalj je i tako nevažan, dosta je raspisati ovo gore. , no taj detalj je i tako nevažan, dosta je raspisati ovo gore.
3. a) je, ako se upotrijebi štos koji sam napisao, jako lagano raspisivanje koje ste morali vidjeti već puno puta na vježbama i nema ništa posebno pametno u njemu.
3. b) se svodi na to da vidimo da nulvektor ne zadovoljava
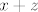 , a svaki potprostor mora sadržavati nulvektor dakle kraj. , a svaki potprostor mora sadržavati nulvektor dakle kraj.
Ako postoji 1 protuprimjer, postoji ih beskonačno, ideja je da prepoznate da uvjet
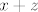
NIJE linearan, dakle ovo nije potprostor, i onda počnete tražiti protuprimjer ili, alternativno, počnete dokazivati da je i zapnete pa se onda zapitate je li stvarno.
_________________
Ceterum censeo Carthaginem esse delendam.
|
|
| [Vrh] |
|
helga
Forumaš(ica)


Pridružen/a: 01. 11. 2011. (22:24:33)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
helga
Forumaš(ica)


Pridružen/a: 01. 11. 2011. (22:24:33)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 17:18 ned, 6. 11. 2011 Naslov: Postano: 17:18 ned, 6. 11. 2011 Naslov: |
    |
|
|
[quote="helga"]Hm, pod [b]a)[/b] mi jedan od uvjeta bude[b] γ(λ+4)=0.[/b]
Budući da oni moraju biti linearno nezavisni, a to su akko su α=β=γ=0, znači li to da λ može biti bilo koji element iz R ili da sam ja nešto fulala? :shock:[/quote]
okej, dobro ti je to. i sada imaš γ(λ+4)=0 i kada će ti to biti jednako 0?? akko je λ+4 različito od 0, tj λ različita od -4
| helga (napisa): | Hm, pod a) mi jedan od uvjeta bude γ(λ+4)=0.
Budući da oni moraju biti linearno nezavisni, a to su akko su α=β=γ=0, znači li to da λ može biti bilo koji element iz R ili da sam ja nešto fulala?  |
okej, dobro ti je to. i sada imaš γ(λ+4)=0 i kada će ti to biti jednako 0?? akko je λ+4 različito od 0, tj λ različita od -4
|
|
| [Vrh] |
|
helga
Forumaš(ica)


Pridružen/a: 01. 11. 2011. (22:24:33)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
sasha.f
Forumaš(ica)

Pridružen/a: 25. 10. 2011. (20:04:19)
Postovi: (3D)16
|
|
| [Vrh] |
|
|







