|
Pošto si već pročitao rješenje, nemam ja tu što mudrovat nego ga pokušati objasniti. :)
Prebrojavamo popločavanja [latex]1 \cdot (n+2)[/latex] pravokutnika koji su 2-slomljivi.
Ta 2-slomljivost ovdje znači da raspored NE SMIJE počinjati sa kvadrat pa domino, jer onda ne bi mogli ''prelomiti'' pravokutnik.
Znači, ta prva dva mjesta možemo pokriti sa kvadrat + kvadrat, ili sa jednom dominom - a ostalih n mjesta na [latex]J_n[/latex] načina... Tako dolazimo do [latex]2J_n[/latex] na lijevoj strani.
E sad, podijelimo na dva slučaja - ovisno je li drugi po redu kvadrat ili domina (pazi, ne na drugom mjestu, već druga po redu pločica).
Ako je domina druga po redu:
-zbog 2-slomljivosti kombinacija kvadrat + domina nije dopuštena, pa i na prvom mjestu mora biti domina
Znači, prva 4 polja znamo kako popločati (sa dvije domine), tako dolazimo do [latex]J_{n + 2 - 4} = J_{n-2}[/latex] popločavanja.
Ako je kvadrat drugi po redu:
- 2-slomljivosti ''ne smeta'' ni kombinacija domina + kvadrat ni kvadrat + kvadrat
Znači, taj kvadrat možemo zanemariti, tj. napraviti bijekciju sa [latex]1 \cdot (n+1)[/latex] preslikavanjem - tako dolazimo do
[latex]J_{n+1}[/latex].
Vjerujem da je ovo možda najviše nejasan korak, ali to si već sigurno zamijetio u diskretnoj - ako nešto ''moramo'' napraviti (kao što ovdje kvadrat mora biti druga pločica) to i ne brojimo, da se malo slobodnije izrazim.
Pošto si već pročitao rješenje, nemam ja tu što mudrovat nego ga pokušati objasniti. 
Prebrojavamo popločavanja 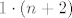 pravokutnika koji su 2-slomljivi. pravokutnika koji su 2-slomljivi.
Ta 2-slomljivost ovdje znači da raspored NE SMIJE počinjati sa kvadrat pa domino, jer onda ne bi mogli ''prelomiti'' pravokutnik.
Znači, ta prva dva mjesta možemo pokriti sa kvadrat + kvadrat, ili sa jednom dominom - a ostalih n mjesta na 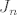 načina... Tako dolazimo do načina... Tako dolazimo do 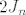 na lijevoj strani. na lijevoj strani.
E sad, podijelimo na dva slučaja - ovisno je li drugi po redu kvadrat ili domina (pazi, ne na drugom mjestu, već druga po redu pločica).
Ako je domina druga po redu:
-zbog 2-slomljivosti kombinacija kvadrat + domina nije dopuštena, pa i na prvom mjestu mora biti domina
Znači, prva 4 polja znamo kako popločati (sa dvije domine), tako dolazimo do 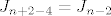 popločavanja. popločavanja.
Ako je kvadrat drugi po redu:
- 2-slomljivosti ''ne smeta'' ni kombinacija domina + kvadrat ni kvadrat + kvadrat
Znači, taj kvadrat možemo zanemariti, tj. napraviti bijekciju sa 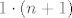 preslikavanjem - tako dolazimo do preslikavanjem - tako dolazimo do
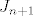 . .
Vjerujem da je ovo možda najviše nejasan korak, ali to si već sigurno zamijetio u diskretnoj - ako nešto ''moramo'' napraviti (kao što ovdje kvadrat mora biti druga pločica) to i ne brojimo, da se malo slobodnije izrazim.
|




