|
Ide rješenje, mislim da je točno.
Neka su [latex]a_1, a_2, ... a_n[/latex] realni brojevi takvi da je [latex]a_1<a_2<a_3<...<a_n[/latex] te vrijedi [latex]f(a_1)=f(a_2)=...=f(a_n)[/latex].
Analogno definiramo brojeve [latex]b_1, b_2, ..., b_n[/latex].
(Znamo da funkcija ima [latex]n[/latex] rješenja jednadžbe [latex]f(x)=a[/latex]. To znamo ili po slici ili intuitivno: na intervalu [latex]<-\infty , c_1>[/latex] funkcija je negativna, na intervalu [latex]<c_n, +\infty>[/latex] funkcija je pozitivna, pada od beskonačnosti i približava se nuli, a za svaki interval [latex]<c_i, c_{i+1}>[/latex] funkcija počinje padati od beskonačnosti (blizu pravca [latex]x=c_i[/latex]), prema -beskonačnosti (uz pravac [latex]x=c_{i+1}[/latex]. Nisam rekao, no jasno je da su pravci [latex]x=c_i[/latex] i [latex]y=0[/latex] asimptote.)
Tada je jasno da je tražena duljina intervala jednaka [latex](a_1-b_1)+(a_2-b_2)+...+(a_n-b_n)= \sum_{i=1}^{n}{a_i} - \sum_{i=1}^{n}{b_i}[/latex]
(Ovdje bi po mojem mišljenju trebala ići malo bolja argumentacija, ali kao što rekoh, sve je jasno sa slike.)
Rješavamo jednadžbu [latex]f(x)=a[/latex].
[latex]a=f(x)=\sum_{i=1}^{n}{\frac{1}{x-c_i}}[/latex]
Sad ću sve pomnožiti s nazivnicima s desne strane i podijeliti s [latex]a[/latex]. U tu svrhu uvodim oznake:
[latex]P_i(x)=(x-c_1)(x-c_2)...(x-c_{i-2})(x-c_{i-1})(x-c_{i+1})(x-c_{i+2})...(x-c_{n})[/latex], [latex]\forall i \in \{1, ..., n \}[/latex] (tj. umnožak svih osim [latex](x-c_{i})[/latex] ).
[latex]Q(x)=(x-c_1)(x-c_2)...(x-c_n)[/latex].
Tada je početna jednakost ekvivalentna sljedećoj:
[latex]Q(x)=\frac{P_1(x)+P_2(x)+...+P_n(x)}{a}[/latex]
[latex]Q(x)-\frac{P_1(x)+P_2(x)+...+P_n(x)}{a}=0[/latex].
Nas zapravo zanima suma rješenja ove jednadžbe. Pošto smo opet s lijeve strane dobili polinom, prema Vieti trebamo samo odrediti koeficijent uz [latex]x^{n-1}[/latex].
U polinomu [latex]Q(x)[/latex] to je [latex]-\sum_{i=1}^{n}{c_i}[/latex] (opet korištenje Viete). U polinomima [latex]P_i(x)[/latex] to je vodeći koeficijent, i to 1.
Dakle suma rješenja je [latex]\sum_{i=1}^{n}{a_i}=\sum_{i=1}^{n}{c_i}+\frac{n}{a}[/latex].
Analogno, [latex]\sum_{i=1}^{n}{b_i}=\sum_{i=1}^{n}{c_i}+\frac{n}{b}[/latex].
Sada je tražena ukupna duljina intervala zapravo razlika tih dviju suma, a to je [latex]n ( \frac{1}{a} - \frac{1}{b} )[/latex].
Ide rješenje, mislim da je točno.
Neka su 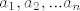 realni brojevi takvi da je realni brojevi takvi da je 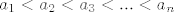 te vrijedi te vrijedi 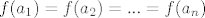 . .
Analogno definiramo brojeve 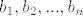 . .
(Znamo da funkcija ima  rješenja jednadžbe rješenja jednadžbe 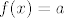 . To znamo ili po slici ili intuitivno: na intervalu . To znamo ili po slici ili intuitivno: na intervalu 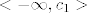 funkcija je negativna, na intervalu funkcija je negativna, na intervalu 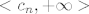 funkcija je pozitivna, pada od beskonačnosti i približava se nuli, a za svaki interval funkcija je pozitivna, pada od beskonačnosti i približava se nuli, a za svaki interval 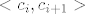 funkcija počinje padati od beskonačnosti (blizu pravca funkcija počinje padati od beskonačnosti (blizu pravca 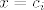 ), prema -beskonačnosti (uz pravac ), prema -beskonačnosti (uz pravac 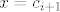 . Nisam rekao, no jasno je da su pravci . Nisam rekao, no jasno je da su pravci 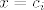 i i 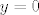 asimptote.) asimptote.)
Tada je jasno da je tražena duljina intervala jednaka 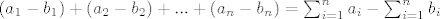
(Ovdje bi po mojem mišljenju trebala ići malo bolja argumentacija, ali kao što rekoh, sve je jasno sa slike.)
Rješavamo jednadžbu 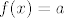 . .
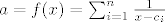
Sad ću sve pomnožiti s nazivnicima s desne strane i podijeliti s  . U tu svrhu uvodim oznake: . U tu svrhu uvodim oznake:
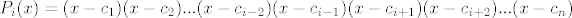 , , 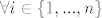 (tj. umnožak svih osim (tj. umnožak svih osim  ). ).
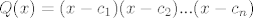 . .
Tada je početna jednakost ekvivalentna sljedećoj:
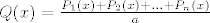
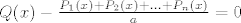 . .
Nas zapravo zanima suma rješenja ove jednadžbe. Pošto smo opet s lijeve strane dobili polinom, prema Vieti trebamo samo odrediti koeficijent uz 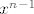 . .
U polinomu 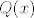 to je to je 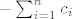 (opet korištenje Viete). U polinomima (opet korištenje Viete). U polinomima 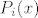 to je vodeći koeficijent, i to 1. to je vodeći koeficijent, i to 1.
Dakle suma rješenja je 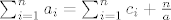 . .
Analogno, 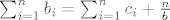 . .
Sada je tražena ukupna duljina intervala zapravo razlika tih dviju suma, a to je 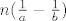 . .
|





