|
Od jednog kolege nedavno dobih nekoliko pitanja o povezanosti i povezanosti putovima. Mislim da tu ima stvari koje bi mogle zanimati i širu javnost, pa evo, kad je već natipkano:
1. Otvoren skup u [latex]\mathbb{R}^n[/latex] je povezan akko je povezan putovima.
Dokaz: Znamo da za proizvoljan [latex]A \subset \mathbb{R}^n[/latex] vrijedi da, ako je povezan putevima, onda je i povezan (Korolar 8.8 ).
Obrat nažalost nije toliko lagan ili, bolje rečeno, jest lagan, i prilično elegantan :), ali prvo moramo malo bolje razmisliti općenito o povezanosti putovima, tj. uočiti da je povezanost putovima relacija ekvivalencije na skupu [latex]A[/latex] (ovdje je za dani [latex]A \subset \mathbb{R}^n[/latex] relacija povezanosti putovima na [latex]A[/latex] definirana sa: x i y iz [latex]A[/latex] su povezane putom akko postoji put u [latex]A[/latex] od x do y). Stvarno:
- refleksivnost: svaka točka x povezana je putom sa samom sobom; primjer puta od x do x je
[latex]f:[0,1] \to A \quad f(t) = x[/latex];
- simetričnost: ako je x povezana putom sa y, onda je i y povezana putom sa x:
ako je put od x do y [latex]f:[a, b] \to A[/latex] t. d. [latex]f(a) = x, f(b) = y[/latex], onda je [latex]g:[0, 1] \to A \quad g(t) = f(t a + (1 - t)b)[/latex] put od y do x u A (prolazi istim točkama, samo unatrag, pa je sigurno u A);
- tranzitivnost: ako je [latex]f:[a, b] \to A[/latex] put u A od x do y, a [latex]g:[c, d] \to A[/latex] put u A od y do z, onda možemo npr. prvo uočiti da su i
[latex]f_1: [0, 1] \to A \quad f_1(t) := f((1 - t) a + t b)[/latex] i [latex]f_2: [0, 1] \to A \quad f_2(t) := g((1 - t) c + t d)[/latex]
isto putovi u A od x do y, odnosno od y do z, pa je
[latex]h:[0, 1]\to A \quad h(t):=
\begin{cases} f_1(2t) & t \in [0,\frac{1}{2}] \\
f_2(2(t - \frac{1}{2})) & t \in <\frac{1}{2}, 1] \\
\end{cases}[/latex]
put od x do z u A.
OK, zašto nam je to bitno? Pa, znamo da relacija ekvivalencije dijeli skup na kojem je zadana na klase ekvivalencije, tj., u našem slučaju, proizvoljan skup [latex]A \subset \mathbb{R}^n[/latex] relacija povezanosti putovima dijeli na hrpu malih klasa, tj. skupića unutar kojih su bilo koje dvije točke povezane putovima, i nijedna njihova točka nije povezana putom ni s kojom točkom izvana. I sad je očito
skup povezan putovima akko je broj klasa ekvivalencije po relaciji povezanosti putovima jednak 1.
Dakle, mi moramo dokazati da je za otvoren (neprazan) skup u [latex]\mathbb{R}^n[/latex] broj tih klasa ekvivalencije točno 1.
Neka je A otvoren u [latex]\mathbb{R}^n[/latex]. Prvo uočimo da je tada svaka klasa ekvivalencije povezanosti putovima otvoren skup: stvarno, za svaku točku c unutar te klase ekvivalencije zbog otvorenosti skupa A postoji otvorena kugla sa središtem u c koja je cijela sadržana u A. Kako su otvorene kugle povezane putovima, onda je i ta naša kugla oko c povezana putovima. Posebno, sve su njene točke povezane putovima sa c, pa se nalaze u klasi ekvivalencije u kojoj se nalazi i c, dakle cijela je kugla oko c sadržana u njenoj klasi ekvivalencije.
Dakle, pokazali smo da oko svake točke c postoji cijela kugla sa središtem u c koja je sadržana u našoj klasi ekvivalencije, dakle ta je klasa otvoren skup.
I sad napokon imamo sve što nam treba:
pretpostavimo da A nije povezan putovima, tj. da je broj klasa ekvivalencije (koje su po definiciji klasa ekvivalencije neprazni skupovi) > 1. Odaberimo jednu i nazovimo je B, a sa C označimo uniju svih preostalih klasa. Očito je B po ovome gore otvoren skup, C je unija otvorenih pa je također otvoren, i B i C su neprazni i u uniji daju cijeli A [latex]\Rightarrow[/latex] A nije povezan!
Kraj.
Uočimo još samo da je bilo bitno da A bude otvoren kako bi klase ekvivalencije bile otvorene, inače ništa od dokaza.
2. Ako je [latex]A \subset \mathbb{R}^n[/latex] povezan, onda je i njegov zatvarač povezan.
Pretpostavimo da je [latex]\overline{A} = B \cup C[/latex], gdje su B i C disjunktni, zatvoreni u [latex]\overline{A}[/latex] i u uniji daju cijeli [latex]\overline{A}[/latex]. Želimo pokazati da je bar jedan od njih prazan skup.
Prvo uočimo da su [latex]B \cap A[/latex] i [latex]C \cap A[/latex] zatvoreni u A, disjunktni i u uniji daju cijeli A. Kako je A povezan, barem je jedan od njih prazan skup, BSO [latex]C \cap A[/latex]. Onda mora biti [latex]B \cap A = A[/latex]. Posebno, imamo
[latex]A \subset B \quad \Rightarrow \quad \overline{A} \subset \overline{B} = B[/latex]
(pri čemu su zatvarači na desnoj strani zatvarači u relativnoj topologiji induciranoj sa [latex]\overline{A}[/latex]. Odavde je [latex]\overline{A} = B[/latex], ali onda jadan C ostaje prazan. A to smo i htjeli.
Nap: Ovdje je korištena "lema": Ako je [latex]A \subset \mathbb{R}^n[/latex] i [latex]B \subset A[/latex] te S skup otvoren (zatvoren) u A, onda je [latex]S \cap B[/latex] otvoren (zatvoren) u B.
3. (Prop. 8. 14.): Ako je [latex]A_i, i \in I[/latex] familija povezanih podskupova od [latex]\mathbb{R}^n[/latex] koji svi sadrže istu točku c, onda je i njihova unija povezan skup.
Dokaz: Zovimo tu uniju S.
Pretpostavimo suprotno, da postoje skupovi B i C koji su otvoreni u S, disjunktni, neprazni i u uniji daju cijeli S. Tada se točka c nalazi točno u jednom od njih, BSO u C.
B je neprazan. Odaberimo neku točku [latex]b \in B[/latex]. Ona se nalazi u nekom [latex]A_i[/latex]-u. E sad, imamo
[latex]B \cap A_i \neq \emptyset \quad[/latex] jer je b unutra,
[latex]C \cap A_i \neq \emptyset \quad[/latex] jer je c unutra (c je u svim [latex]A_i[/latex]-evima);
[latex]B \cap A_i[/latex] i [latex]C \cap A_i[/latex] su otvoreni u [latex]A_i[/latex], disjunktni i u uniji daju cijeli [latex]A_i \quad \Rightarrow \quad A_i[/latex] nije povezan. Kontradikcija!
Nap: Ista propozicija vrijedi i ako povezanost zamijenimo povezanošću putovima, a onda ju je još lakše dokazati: jednostavno se iskoristi da je svaka točka unije povezana putom sa c, a onda tranzitivnost povezanosti putovima, i to je to.
Ako u cijeloj ovoj priči nađete neku rupu, grešku ili ljepši dokaz, objavite, za opće dobro! :roll:
Od jednog kolege nedavno dobih nekoliko pitanja o povezanosti i povezanosti putovima. Mislim da tu ima stvari koje bi mogle zanimati i širu javnost, pa evo, kad je već natipkano:
1. Otvoren skup u  je povezan akko je povezan putovima. je povezan akko je povezan putovima.
Dokaz: Znamo da za proizvoljan 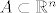 vrijedi da, ako je povezan putevima, onda je i povezan (Korolar 8.8 ). vrijedi da, ako je povezan putevima, onda je i povezan (Korolar 8.8 ).
Obrat nažalost nije toliko lagan ili, bolje rečeno, jest lagan, i prilično elegantan  , ali prvo moramo malo bolje razmisliti općenito o povezanosti putovima, tj. uočiti da je povezanost putovima relacija ekvivalencije na skupu , ali prvo moramo malo bolje razmisliti općenito o povezanosti putovima, tj. uočiti da je povezanost putovima relacija ekvivalencije na skupu  (ovdje je za dani (ovdje je za dani 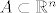 relacija povezanosti putovima na relacija povezanosti putovima na  definirana sa: x i y iz definirana sa: x i y iz  su povezane putom akko postoji put u su povezane putom akko postoji put u  od x do y). Stvarno: od x do y). Stvarno:
- refleksivnost: svaka točka x povezana je putom sa samom sobom; primjer puta od x do x je
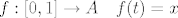 ; ;
- simetričnost: ako je x povezana putom sa y, onda je i y povezana putom sa x:
ako je put od x do y 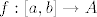 t. d. t. d. 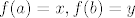 , onda je , onda je 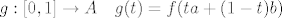 put od y do x u A (prolazi istim točkama, samo unatrag, pa je sigurno u A); put od y do x u A (prolazi istim točkama, samo unatrag, pa je sigurno u A);
- tranzitivnost: ako je 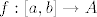 put u A od x do y, a put u A od x do y, a 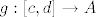 put u A od y do z, onda možemo npr. prvo uočiti da su i put u A od y do z, onda možemo npr. prvo uočiti da su i
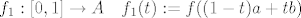 i i 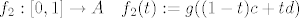
isto putovi u A od x do y, odnosno od y do z, pa je
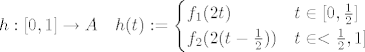
put od x do z u A.
OK, zašto nam je to bitno? Pa, znamo da relacija ekvivalencije dijeli skup na kojem je zadana na klase ekvivalencije, tj., u našem slučaju, proizvoljan skup 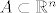 relacija povezanosti putovima dijeli na hrpu malih klasa, tj. skupića unutar kojih su bilo koje dvije točke povezane putovima, i nijedna njihova točka nije povezana putom ni s kojom točkom izvana. I sad je očito relacija povezanosti putovima dijeli na hrpu malih klasa, tj. skupića unutar kojih su bilo koje dvije točke povezane putovima, i nijedna njihova točka nije povezana putom ni s kojom točkom izvana. I sad je očito
skup povezan putovima akko je broj klasa ekvivalencije po relaciji povezanosti putovima jednak 1.
Dakle, mi moramo dokazati da je za otvoren (neprazan) skup u  broj tih klasa ekvivalencije točno 1. broj tih klasa ekvivalencije točno 1.
Neka je A otvoren u  . Prvo uočimo da je tada svaka klasa ekvivalencije povezanosti putovima otvoren skup: stvarno, za svaku točku c unutar te klase ekvivalencije zbog otvorenosti skupa A postoji otvorena kugla sa središtem u c koja je cijela sadržana u A. Kako su otvorene kugle povezane putovima, onda je i ta naša kugla oko c povezana putovima. Posebno, sve su njene točke povezane putovima sa c, pa se nalaze u klasi ekvivalencije u kojoj se nalazi i c, dakle cijela je kugla oko c sadržana u njenoj klasi ekvivalencije. . Prvo uočimo da je tada svaka klasa ekvivalencije povezanosti putovima otvoren skup: stvarno, za svaku točku c unutar te klase ekvivalencije zbog otvorenosti skupa A postoji otvorena kugla sa središtem u c koja je cijela sadržana u A. Kako su otvorene kugle povezane putovima, onda je i ta naša kugla oko c povezana putovima. Posebno, sve su njene točke povezane putovima sa c, pa se nalaze u klasi ekvivalencije u kojoj se nalazi i c, dakle cijela je kugla oko c sadržana u njenoj klasi ekvivalencije.
Dakle, pokazali smo da oko svake točke c postoji cijela kugla sa središtem u c koja je sadržana u našoj klasi ekvivalencije, dakle ta je klasa otvoren skup.
I sad napokon imamo sve što nam treba:
pretpostavimo da A nije povezan putovima, tj. da je broj klasa ekvivalencije (koje su po definiciji klasa ekvivalencije neprazni skupovi) > 1. Odaberimo jednu i nazovimo je B, a sa C označimo uniju svih preostalih klasa. Očito je B po ovome gore otvoren skup, C je unija otvorenih pa je također otvoren, i B i C su neprazni i u uniji daju cijeli A  A nije povezan! A nije povezan!
Kraj.
Uočimo još samo da je bilo bitno da A bude otvoren kako bi klase ekvivalencije bile otvorene, inače ništa od dokaza.
2. Ako je 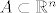 povezan, onda je i njegov zatvarač povezan. povezan, onda je i njegov zatvarač povezan.
Pretpostavimo da je 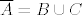 , gdje su B i C disjunktni, zatvoreni u , gdje su B i C disjunktni, zatvoreni u 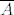 i u uniji daju cijeli i u uniji daju cijeli 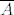 . Želimo pokazati da je bar jedan od njih prazan skup. . Želimo pokazati da je bar jedan od njih prazan skup.
Prvo uočimo da su  i i  zatvoreni u A, disjunktni i u uniji daju cijeli A. Kako je A povezan, barem je jedan od njih prazan skup, BSO zatvoreni u A, disjunktni i u uniji daju cijeli A. Kako je A povezan, barem je jedan od njih prazan skup, BSO  . Onda mora biti . Onda mora biti 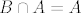 . Posebno, imamo . Posebno, imamo

(pri čemu su zatvarači na desnoj strani zatvarači u relativnoj topologiji induciranoj sa 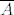 . Odavde je . Odavde je 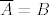 , ali onda jadan C ostaje prazan. A to smo i htjeli. , ali onda jadan C ostaje prazan. A to smo i htjeli.
Nap: Ovdje je korištena "lema": Ako je 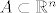 i i 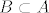 te S skup otvoren (zatvoren) u A, onda je te S skup otvoren (zatvoren) u A, onda je  otvoren (zatvoren) u B. otvoren (zatvoren) u B.
3. (Prop. 8. 14.): Ako je 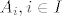 familija povezanih podskupova od familija povezanih podskupova od  koji svi sadrže istu točku c, onda je i njihova unija povezan skup. koji svi sadrže istu točku c, onda je i njihova unija povezan skup.
Dokaz: Zovimo tu uniju S.
Pretpostavimo suprotno, da postoje skupovi B i C koji su otvoreni u S, disjunktni, neprazni i u uniji daju cijeli S. Tada se točka c nalazi točno u jednom od njih, BSO u C.
B je neprazan. Odaberimo neku točku 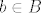 . Ona se nalazi u nekom . Ona se nalazi u nekom 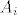 -u. E sad, imamo -u. E sad, imamo
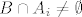 jer je b unutra, jer je b unutra,
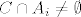 jer je c unutra (c je u svim jer je c unutra (c je u svim 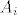 -evima); -evima);
 i i 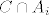 su otvoreni u su otvoreni u 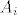 , disjunktni i u uniji daju cijeli , disjunktni i u uniji daju cijeli 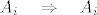 nije povezan. Kontradikcija! nije povezan. Kontradikcija!
Nap: Ista propozicija vrijedi i ako povezanost zamijenimo povezanošću putovima, a onda ju je još lakše dokazati: jednostavno se iskoristi da je svaka točka unije povezana putom sa c, a onda tranzitivnost povezanosti putovima, i to je to.
Ako u cijeloj ovoj priči nađete neku rupu, grešku ili ljepši dokaz, objavite, za opće dobro! 
|




