| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 10:11 pon, 31. 10. 2011 Naslov: Postano: 10:11 pon, 31. 10. 2011 Naslov: |
    |
|
|
Evo, dakle 6. zadatak pod c...
Znači, išao sam tako što sam prvo odredio funkciju distribucije od Z,
to derivirao i dobije se funkcija gustoće.
Vjerojatno se može i direktno uvrštavajući u formule iz šalabahtera, ali tamo
daju od Y/X, dok mi ovdje imamo X/Y, pa sam nešto spetljao.
Ovo je možda malo duži način, ali znam da funkcionira :D
Dakle, B grupa npr.:
Primijeti se da je funkcija distribucije definirana samo za z > 0, inače imamo da je nešto pozitivno manje od nečeg negativnog (to baš
ne želimo)...
[latex]P(Z < z) = P (X / Y < z) = \int_{0}^{\infty} \int_{0}^{yz} \lambda \mu e^{-\lambda x - \mu y} dx\,dy = ... = 1 - \frac{\mu}{\lambda z + \mu}, z > 0[/latex]
I sad se to derivira i dobije se rezultat :D
Za A grupu je potpuno analogno.
Evo, dakle 6. zadatak pod c...
Znači, išao sam tako što sam prvo odredio funkciju distribucije od Z,
to derivirao i dobije se funkcija gustoće.
Vjerojatno se može i direktno uvrštavajući u formule iz šalabahtera, ali tamo
daju od Y/X, dok mi ovdje imamo X/Y, pa sam nešto spetljao.
Ovo je možda malo duži način, ali znam da funkcionira 
Dakle, B grupa npr.:
Primijeti se da je funkcija distribucije definirana samo za z > 0, inače imamo da je nešto pozitivno manje od nečeg negativnog (to baš
ne želimo)...
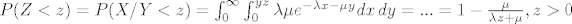
I sad se to derivira i dobije se rezultat 
Za A grupu je potpuno analogno.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|






