| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Zbunjeni
Forumaš(ica)
Pridružen/a: 25. 01. 2011. (12:36:22)
Postovi: (9)16
|
|
| [Vrh] |
|
ebartos
Forumaš(ica)
Pridružen/a: 02. 10. 2011. (10:37:27)
Postovi: (A)16
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
 Postano: 18:32 sub, 17. 12. 2011 Naslov: Postano: 18:32 sub, 17. 12. 2011 Naslov: |
    |
|
|
[quote="pedro"]http://web.math.hr/nastava/la/DZ/la1-1112-dz3.pdf
može prvi zad?[/quote]
domena su parne permutacije tj. broj njihovih inverzija je paran broj. Funkcija uzima jednu parnu permutaciju i komponira ju sa neparnom permutacijom, posto kodomenu cine neparne permutacije kompozicija mora biti neparna, a ako kompozicija nije neparna permutacija onda funkcija nije dobro definirana jer joj je slika veća od kodomena. Trebas provjeriti je li kompozicija neparna, a to provjeris preko signuma, posto vrijedi:
sign(pq)=sing(p)*sing(q),
sign parnih permutacija je 1 a neparnih -1 dobis da je sing(pq)=-1 tj. funkcija je dobro defnirana
nisam posve siguran, volio bih da netko potvrdi tocnost/netocnost ovog rjesenja.
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
sign* :)
| pedro (napisa): | http://web.math.hr/nastava/la/DZ/la1-1112-dz3.pdf
može prvi zad? |
domena su parne permutacije tj. broj njihovih inverzija je paran broj. Funkcija uzima jednu parnu permutaciju i komponira ju sa neparnom permutacijom, posto kodomenu cine neparne permutacije kompozicija mora biti neparna, a ako kompozicija nije neparna permutacija onda funkcija nije dobro definirana jer joj je slika veća od kodomena. Trebas provjeriti je li kompozicija neparna, a to provjeris preko signuma, posto vrijedi:
sign(pq)=sing(p)*sing(q),
sign parnih permutacija je 1 a neparnih -1 dobis da je sing(pq)=-1 tj. funkcija je dobro defnirana
nisam posve siguran, volio bih da netko potvrdi tocnost/netocnost ovog rjesenja.
Added after 1 minutes:
sign* 
_________________
it was merely a setback
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:04 sub, 17. 12. 2011 Naslov: Postano: 19:04 sub, 17. 12. 2011 Naslov: |
    |
|
|
[quote="Shaman"][quote="pedro"]http://web.math.hr/nastava/la/DZ/la1-1112-dz3.pdf
može prvi zad?[/quote]
domena su parne permutacije tj. broj njihovih inverzija je paran broj. Funkcija uzima jednu parnu permutaciju i komponira ju sa neparnom permutacijom, posto kodomenu cine neparne permutacije kompozicija mora biti neparna, a ako kompozicija nije neparna permutacija onda funkcija nije dobro definirana jer joj je slika veća od kodomena. Trebas provjeriti je li kompozicija neparna, a to provjeris preko signuma, posto vrijedi:
sign(pq)=sing(p)*sing(q),
sign parnih permutacija je 1 a neparnih -1 dobis da je sing(pq)=-1 tj. funkcija je dobro defnirana
nisam posve siguran, volio bih da netko potvrdi tocnost/netocnost ovog rjesenja.
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
sign* :)[/quote]
Potrebno je još dokazati da je [tex]\varphi_q[/tex] bijekcija. Dovoljno je pokazati da je injekcija (zašto?).
| Shaman (napisa): | | pedro (napisa): | http://web.math.hr/nastava/la/DZ/la1-1112-dz3.pdf
može prvi zad? |
domena su parne permutacije tj. broj njihovih inverzija je paran broj. Funkcija uzima jednu parnu permutaciju i komponira ju sa neparnom permutacijom, posto kodomenu cine neparne permutacije kompozicija mora biti neparna, a ako kompozicija nije neparna permutacija onda funkcija nije dobro definirana jer joj je slika veća od kodomena. Trebas provjeriti je li kompozicija neparna, a to provjeris preko signuma, posto vrijedi:
sign(pq)=sing(p)*sing(q),
sign parnih permutacija je 1 a neparnih -1 dobis da je sing(pq)=-1 tj. funkcija je dobro defnirana
nisam posve siguran, volio bih da netko potvrdi tocnost/netocnost ovog rjesenja.
Added after 1 minutes:
sign*  |
Potrebno je još dokazati da je [tex]\varphi_q[/tex] bijekcija. Dovoljno je pokazati da je injekcija (zašto?).
_________________
The Dude Abides
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 19:24 sub, 17. 12. 2011 Naslov: Postano: 19:24 sub, 17. 12. 2011 Naslov: |
    |
|
|
3 zad.
uocimo da zadatak ima smisla za n>=2 (jer za n=1 ne postoji neparna permutacija q). pokazat cemo da su [latex]A_n[/latex] i [latex]B_n[/latex] jednakobrojni skupovi, i da je [latex]\varphi_q[/latex] injekcija, odakle slijedi da je i bijekcija (injekcija izmedu jednakobrojni konacnih skupovi je i surjekcija, pa i bijekcija). Da bi pokazali da su [latex]A_n[/latex] i [latex]B_n[/latex] jednakobrojni, pogledajmo ova dva preslikavanja : ako je [latex]p[/latex] parna permutacija, zamijeni ono u sto permutacija baca (12). na primjer, ako je p(1 2 3 4 5) = (3 5 2 1 4), zamijenimo 3 5 i dobijemo (5 3 2 1 4). ovako smo iz parne permutacije dobili neparnu. Sad ako je p neparna permutacija, napravi istu stvar i dobijemo parnu permutaciju. Dakle imamo injektivnu funkciju iz [latex]A_n[/latex] u [latex]B_n[/latex] i injektivnu funkciju u drugom smjeru, pa je [latex]|A_n| \leq |B_n|[/latex] i [latex]|A_n| \geq |B_n|[/latex] => [latex]|A_n| = |B_n|[/latex].
Sad da bi pokazali da je [latex]\varphi_q[/latex] injekcija, pretpostavimo da je [latex]\varphi_q(p_1) = \varphi_q(p_2)[/latex] odnosno [latex]p_1q = p_2q[/latex]. komponiramo zdesna sa [latex]q^{-1}[/latex] (svaka permutacija ima inverz) pa dobivamo [latex]p_1 = p_2[/latex], dakle funkcija je injekcija.
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
i [latex]\varphi_q[/latex] je dobro definirano jer je kompozicija parne i neparne permutacije neparna permutacija (jer je sgn(pq) = sgn(p)*sgn(q) = 1*-1 = -1)
vidim da je dosta ljudi vec odgovorilo dok sam ja to natipkao, a sta ces :D
3 zad.
uocimo da zadatak ima smisla za n>=2 (jer za n=1 ne postoji neparna permutacija q). pokazat cemo da su 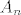 i i 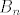 jednakobrojni skupovi, i da je jednakobrojni skupovi, i da je 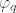 injekcija, odakle slijedi da je i bijekcija (injekcija izmedu jednakobrojni konacnih skupovi je i surjekcija, pa i bijekcija). Da bi pokazali da su injekcija, odakle slijedi da je i bijekcija (injekcija izmedu jednakobrojni konacnih skupovi je i surjekcija, pa i bijekcija). Da bi pokazali da su 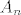 i i 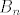 jednakobrojni, pogledajmo ova dva preslikavanja : ako je jednakobrojni, pogledajmo ova dva preslikavanja : ako je  parna permutacija, zamijeni ono u sto permutacija baca (12). na primjer, ako je p(1 2 3 4 5) = (3 5 2 1 4), zamijenimo 3 5 i dobijemo (5 3 2 1 4). ovako smo iz parne permutacije dobili neparnu. Sad ako je p neparna permutacija, napravi istu stvar i dobijemo parnu permutaciju. Dakle imamo injektivnu funkciju iz parna permutacija, zamijeni ono u sto permutacija baca (12). na primjer, ako je p(1 2 3 4 5) = (3 5 2 1 4), zamijenimo 3 5 i dobijemo (5 3 2 1 4). ovako smo iz parne permutacije dobili neparnu. Sad ako je p neparna permutacija, napravi istu stvar i dobijemo parnu permutaciju. Dakle imamo injektivnu funkciju iz 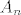 u u 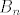 i injektivnu funkciju u drugom smjeru, pa je i injektivnu funkciju u drugom smjeru, pa je 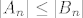 i i 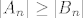 ⇒ ⇒ 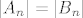 . .
Sad da bi pokazali da je 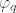 injekcija, pretpostavimo da je injekcija, pretpostavimo da je 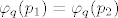 odnosno odnosno  . komponiramo zdesna sa . komponiramo zdesna sa 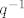 (svaka permutacija ima inverz) pa dobivamo (svaka permutacija ima inverz) pa dobivamo 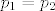 , dakle funkcija je injekcija. , dakle funkcija je injekcija.
Added after 2 minutes:
i 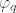 je dobro definirano jer je kompozicija parne i neparne permutacije neparna permutacija (jer je sgn(pq) = sgn(p)*sgn(q) = 1*-1 = -1) je dobro definirano jer je kompozicija parne i neparne permutacije neparna permutacija (jer je sgn(pq) = sgn(p)*sgn(q) = 1*-1 = -1)
vidim da je dosta ljudi vec odgovorilo dok sam ja to natipkao, a sta ces 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
 Postano: 16:51 ned, 18. 12. 2011 Naslov: Postano: 16:51 ned, 18. 12. 2011 Naslov: |
    |
|
|
mislim da se moze 5. dokazat i preko def. umnoska. neka ti je AB=[d(ij)], d(ij)=suma(l=1,...,n)a(il)*b(lj), i=1,...,n, j=1,...,n. Jer je matrica AB opet kvadratna, onda je i=j pa imas d(ij)=suma(l=1,...,n)a(il)*b(li)...analogno neka je BA=[e(ij)], e(ij)=suma(p=1,...,n)b(ip)*a(pi). Sad pogledaj sta ti je AB-BA. sumu(p=1,...,n) mozes zamijenit sumom od l, jer 'secu' po istom pa imas da je AB-BA=suma(l=1,...,n)a(il)b(li)-b(il)a(li)...i sad, kad ti je l=i ( to je mjesto dijagonale) slijedi da je suma =0, a to je kontradikcija s tim da su tu jedinice(jer je tako definirana I)... mislim da se moze tako...ako netko moze rec jel to dobro XD :)
mislim da se moze 5. dokazat i preko def. umnoska. neka ti je AB=[d(ij)], d(ij)=suma(l=1,...,n)a(il)*b(lj), i=1,...,n, j=1,...,n. Jer je matrica AB opet kvadratna, onda je i=j pa imas d(ij)=suma(l=1,...,n)a(il)*b(li)...analogno neka je BA=[e(ij)], e(ij)=suma(p=1,...,n)b(ip)*a(pi). Sad pogledaj sta ti je AB-BA. sumu(p=1,...,n) mozes zamijenit sumom od l, jer 'secu' po istom pa imas da je AB-BA=suma(l=1,...,n)a(il)b(li)-b(il)a(li)...i sad, kad ti je l=i ( to je mjesto dijagonale) slijedi da je suma =0, a to je kontradikcija s tim da su tu jedinice(jer je tako definirana I)... mislim da se moze tako...ako netko moze rec jel to dobro XD 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:06 ned, 18. 12. 2011 Naslov: Postano: 17:06 ned, 18. 12. 2011 Naslov: |
    |
|
|
[quote="jema"]mislim da se moze 5. dokazat i preko def. umnoska. neka ti je AB=[d(ij)], d(ij)=suma(l=1,...,n)a(il)*b(lj), i=1,...,n, j=1,...,n. Jer je matrica AB opet kvadratna, onda je i=j pa imas d(ij)=suma(l=1,...,n)a(il)*b(li)...analogno neka je BA=[e(ij)], e(ij)=suma(p=1,...,n)b(ip)*a(pi). Sad pogledaj sta ti je AB-BA. sumu(p=1,...,n) mozes zamijenit sumom od l, jer 'secu' po istom pa imas da je AB-BA=suma(l=1,...,n)a(il)b(li)-b(il)a(li)...i sad, kad ti je l=i ( to je mjesto dijagonale) slijedi da je suma =0, a to je kontradikcija s tim da su tu jedinice(jer je tako definirana I)... mislim da se moze tako...ako netko moze rec jel to dobro XD :)[/quote]
Malo sam se pogubio u zapisu; želiš reći da u kvadratnim matricama oblika AB-BA na dijagonali su uvijek nule? Ako je tako, uzmi onda 2x2 matrice A i B, gdje A ima sve jedinice, a B ima svuda nule osim na mjestu 2x1 gdje je jedinica. Tada AB-BA na mjestu 1x1 ima jedinicu, a na mjestu 2x2 minus jedan.
| jema (napisa): | mislim da se moze 5. dokazat i preko def. umnoska. neka ti je AB=[d(ij)], d(ij)=suma(l=1,...,n)a(il)*b(lj), i=1,...,n, j=1,...,n. Jer je matrica AB opet kvadratna, onda je i=j pa imas d(ij)=suma(l=1,...,n)a(il)*b(li)...analogno neka je BA=[e(ij)], e(ij)=suma(p=1,...,n)b(ip)*a(pi). Sad pogledaj sta ti je AB-BA. sumu(p=1,...,n) mozes zamijenit sumom od l, jer 'secu' po istom pa imas da je AB-BA=suma(l=1,...,n)a(il)b(li)-b(il)a(li)...i sad, kad ti je l=i ( to je mjesto dijagonale) slijedi da je suma =0, a to je kontradikcija s tim da su tu jedinice(jer je tako definirana I)... mislim da se moze tako...ako netko moze rec jel to dobro XD  |
Malo sam se pogubio u zapisu; želiš reći da u kvadratnim matricama oblika AB-BA na dijagonali su uvijek nule? Ako je tako, uzmi onda 2x2 matrice A i B, gdje A ima sve jedinice, a B ima svuda nule osim na mjestu 2x1 gdje je jedinica. Tada AB-BA na mjestu 1x1 ima jedinicu, a na mjestu 2x2 minus jedan.
_________________
The Dude Abides
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
mirta
Forumaš(ica)
Pridružen/a: 27. 10. 2011. (16:39:01)
Postovi: (9)16
|
|
| [Vrh] |
|
patakenjac
Forumaš(ica)
Pridružen/a: 23. 10. 2011. (17:34:05)
Postovi: (2F)16
|
|
| [Vrh] |
|
mirta
Forumaš(ica)
Pridružen/a: 27. 10. 2011. (16:39:01)
Postovi: (9)16
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
 Postano: 21:45 uto, 3. 1. 2012 Naslov: Postano: 21:45 uto, 3. 1. 2012 Naslov: |
    |
|
|
nije vezano uz 3. dz, vec uz 4. XD ako moze hint za 3 zad...ja sam to krenula ovako: AB=[c{ij}] reda mxs (jer je A mxn, B nxs)..i sad r(A)=min{m,n}, r(AB)=min{m,s}...i sad za m<n,m<s je rang jednak...trebam jos pokazat da je r(A)>=s...kako to? i jel ovo uopce dobar put k rjesenju? mozda nesto 'lakse'? XD hvalaa :)
http://web.math.pmf.unizg.hr/nastava/la/DZ/la1-1112-dz4.pdf
nije vezano uz 3. dz, vec uz 4. XD ako moze hint za 3 zad...ja sam to krenula ovako: AB=[c{ij}] reda mxs (jer je A mxn, B nxs)..i sad r(A)=min{m,n}, r(AB)=min{m,s}...i sad za m<n,m<s je rang jednak...trebam jos pokazat da je r(A)>=s...kako to? i jel ovo uopce dobar put k rjesenju? mozda nesto 'lakse'? XD hvalaa 
http://web.math.pmf.unizg.hr/nastava/la/DZ/la1-1112-dz4.pdf
|
|
| [Vrh] |
|
|











