| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 23:57 sub, 8. 10. 2011 Naslov: Postano: 23:57 sub, 8. 10. 2011 Naslov: |
    |
|
|
Naštimaj u koordinatnom sustavu. ;) Za težište vrijedi [tex]T\left(\frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3}\right)[/tex]. Odaberi si prvi trokut na način da dobiješ neke cjelobrojne koordinate težišta, a onda od toga dalje izračunaj koordinate drugog trokuta. Naravno da ih može biti beskonačno mnogo.
Evo primjer: [tex]A(2, 1), B(4, -1), C(6, 3)[/tex] ima težište [tex]T(4, 1)[/tex]. Za drugi trokut to također treba biti težište. Množenjem sa 3 dobiješ da mora biti [tex]x_P+x_R+x_Q = 12, y_P+y_R+y_Q = 3[/tex]. Recimo, trokut sa koordinatama vrhova [tex]P(-2, 2), R(8, -5), Q(6, 6)[/tex].
Naštimaj u koordinatnom sustavu.  Za težište vrijedi [tex]T\left(\frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3}\right)[/tex]. Odaberi si prvi trokut na način da dobiješ neke cjelobrojne koordinate težišta, a onda od toga dalje izračunaj koordinate drugog trokuta. Naravno da ih može biti beskonačno mnogo. Za težište vrijedi [tex]T\left(\frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3}\right)[/tex]. Odaberi si prvi trokut na način da dobiješ neke cjelobrojne koordinate težišta, a onda od toga dalje izračunaj koordinate drugog trokuta. Naravno da ih može biti beskonačno mnogo.
Evo primjer: [tex]A(2, 1), B(4, -1), C(6, 3)[/tex] ima težište [tex]T(4, 1)[/tex]. Za drugi trokut to također treba biti težište. Množenjem sa 3 dobiješ da mora biti [tex]x_P+x_R+x_Q = 12, y_P+y_R+y_Q = 3[/tex]. Recimo, trokut sa koordinatama vrhova [tex]P(-2, 2), R(8, -5), Q(6, 6)[/tex].
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
 Postano: 9:26 ned, 9. 10. 2011 Naslov: Postano: 9:26 ned, 9. 10. 2011 Naslov: |
    |
|
|
Ok, hvala...A jos samo da pitam...npr jel bi mogla nacrtati te trokute ovako:
Dakle, nacrtam neki trokut i povucem mu tezisnice, odredim teziste i to, a taj drugi trokut nacrtati na nacin da su mu vrhovi zapravo polovista stranica prvog trokuta? Da li sad ta dva trokuta imaju isto teziste ili? Ono, mogu li tako nacrtati mozda? Da li to vrijedi? :)
Ok, hvala...A jos samo da pitam...npr jel bi mogla nacrtati te trokute ovako:
Dakle, nacrtam neki trokut i povucem mu tezisnice, odredim teziste i to, a taj drugi trokut nacrtati na nacin da su mu vrhovi zapravo polovista stranica prvog trokuta? Da li sad ta dva trokuta imaju isto teziste ili? Ono, mogu li tako nacrtati mozda? Da li to vrijedi? 
|
|
| [Vrh] |
|
sequestered
Forumaš(ica)

Pridružen/a: 26. 06. 2011. (20:50:28)
Postovi: (4)16
|
 Postano: 10:45 ned, 9. 10. 2011 Naslov: Postano: 10:45 ned, 9. 10. 2011 Naslov: |
    |
|
|
Neka su [latex] A(x_A,y_A), B(x_B,y_B), C(x_C,y_C)[/latex].
Tada koordinate polovišta dužina [latex]AB , BC, AC [/latex] možemo zapisati redom :[latex]P_{AB}= ( \frac{x_A+x_B}{2},\frac{y_A+y_B}{2}), P_{BC}= ( \frac{x_B+x_C}{2},\frac{y_B+y_C}{2}), P_{AC}= ( \frac{x_A+x_C}{2},\frac{y_A+y_C}{2})[/latex].
Pitanje: Vrijedi li jednakost
[latex]T_{ABC}=T_{P_{AB}P_{BC}P_{AC}}[/latex] ?
Izračunajmo koordinate težišta za trokut [latex]P_{AB}P_{BC}P_{AC}[/latex]:
Prema teoremu o težištu trokuta:
[latex]T_{P_{AB}P_{BC}P_{AC}}= (\frac{\frac{x_A+x_B}{2}+ \frac{x_B+x_C}{2}+\frac{x_A+x_C}{2}}{3}, \frac{\frac{y_A+y_B}{2}+ \frac{y_B+y_C}{2}+\frac{y_A+y_C}{2}}{3})[/latex].
Što, koristeći svojstva množenja i zbrajanja možemo zapisati na sljedeći način:
[latex]T_{P_{AB}P_{BC}P_{AC}}= (\frac{\frac{x_A+x_B+x_B+x_C+x_A+x_C}{2}}{3}, \frac{\frac{y_A+y_B+y_B+y_C+y_A+y_C}{2}}{3})[/latex]
[latex]T_{P_{AB}P_{BC}P_{AC}}= (\frac{\frac{2x_A+2x_B+2x_C}{2}}{3}, \frac{\frac{2y_A+2y_B+2y_C}{2}}{3})[/latex]
[latex]T_{P_{AB}P_{BC}P_{AC}}= (\frac{\frac{2(x_A+x_B+x_C)}{2}}{3}, \frac{\frac{2(y_A+y_B+y_C)}{2}}{3})[/latex]
[latex]T_{P_{AB}P_{BC}P_{AC}}= (\frac{x_A+x_B+x_C}{3}, \frac{y_A+y_B+y_C}{3})=T_{ABC}[/latex].
Jednakost vrijedi, no odabirom tih točaka čini mi se kako je odabrana samo jedna klasa takvih trokuta. Iako trenutno nemam primjer, rekao bih da teorem vrijedi i za neke trokute koji nisu elementi te klase.
Ako sam pogriješio, molim nekoga da ispravi moju pogrešku.
Neka su 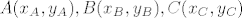 . .
Tada koordinate polovišta dužina 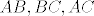 možemo zapisati redom : možemo zapisati redom :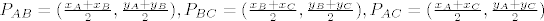 . .
Pitanje: Vrijedi li jednakost
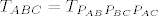 ? ?
Izračunajmo koordinate težišta za trokut 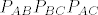 : :
Prema teoremu o težištu trokuta:
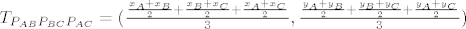 . .
Što, koristeći svojstva množenja i zbrajanja možemo zapisati na sljedeći način:
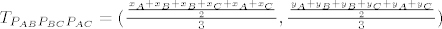
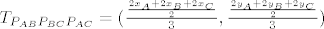
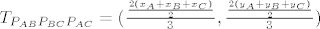
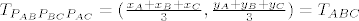 . .
Jednakost vrijedi, no odabirom tih točaka čini mi se kako je odabrana samo jedna klasa takvih trokuta. Iako trenutno nemam primjer, rekao bih da teorem vrijedi i za neke trokute koji nisu elementi te klase.
Ako sam pogriješio, molim nekoga da ispravi moju pogrešku.
|
|
| [Vrh] |
|
tinabg92
Forumaš(ica)

Pridružen/a: 02. 10. 2011. (16:40:51)
Postovi: (5)16
|
|
| [Vrh] |
|
sequestered
Forumaš(ica)

Pridružen/a: 26. 06. 2011. (20:50:28)
Postovi: (4)16
|
 Postano: 19:07 ned, 9. 10. 2011 Naslov: Postano: 19:07 ned, 9. 10. 2011 Naslov: |
    |
|
|
Neka je zadano šest točaka [latex] A, B, C, P, Q, R [/latex] čije su koordinate redom :
[latex] A=(x_A,y_A),B=(x_B,y_B),C=(x_C,y_C) [/latex]
i [latex] P=(x_P,y_P),Q=(x_Q,y_Q),R=(x_R,y_R)
[/latex].
Tada, po teoremu o težištu trokuta vrijede jednakosti:
[latex]T_{ABC}=(\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3})
[/latex] ( za trokut ABC ) i
[latex]T_{PQR}=(\frac{x_P+x_Q+x_R}{3}, \frac{y_P+y_Q+y_R}{3})
[/latex] ( za trokut PQR ).
Tvrdnja koju želimo dokazati :
Ako [latex]AP+BQ+CR=0 [/latex], onda [latex] T_{ABC} = T_{PQR}[/latex].
Tvrdnja se dokazuje direktno.
Pretpostavka: [latex]AP+BQ+CR=0 [/latex].
Zapišimo dani izraz u sljedećem obliku:
[latex](x_P-x_A,y_P-y_A)+(x_Q-x_B,y_Q-y_B)+(x_R-x_C,x_R-y_C)=(0,0)[/latex].
Dvije točke su jednake ako su im pripadajuće koordinate jednake:
[latex]0=(x_P-x_A)+(x_Q-x_B)+(x_R-x_C) [/latex]
[latex]0=(y_P-y_A)+(y_Q-y_B)+(y_R-y_C) [/latex].
Koristeći svojstva zbrajanja, zapišimo u obliku:
[latex]0=x_P+x_Q+x_R-(x_A+x_B+x_C) [/latex]
[latex] 0=y_P+y_Q+y_R-(y_A+y_B+y_C)[/latex].
Dodajmo [latex]x_A+x_B+x_C[/latex] prvoj jednadžbi i
[latex]y_A+y_B+y_C[/latex] drugoj jednadžbi:
[latex]x_A+x_B+x_C=x_P+x_Q+x_R[/latex] i
[latex]y_A+y_B+y_C= y_P+y_Q+y_R[/latex].
Podijelimo dane jednadžbe s [latex]3[/latex]:
[latex]\frac{x_A+x_B+x_C}{3}=\frac{x_P+x_Q+x_R}{3}
[/latex] i
[latex]\frac{y_A+y_B+y_C}{3}=\frac{y_P+y_Q+y_R}{3}
[/latex].
Dvije točke su jednake kada su im pripadajuće koordinate jednake:
[latex](\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3})=(\frac{x_P+x_Q+x_R}{3}, \frac{y_P+y_Q+y_R}{3})
[/latex].
Što možemo zapisati na sljedeći način:
[latex] T_{ABC} = T_{PQR}[/latex].
Ukoliko sam negdje pogriješio, nadam se da će netko tu pogrešku ispraviti.
Neka je zadano šest točaka 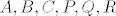 čije su koordinate redom : čije su koordinate redom :
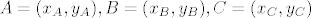
i 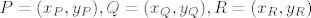 . .
Tada, po teoremu o težištu trokuta vrijede jednakosti:
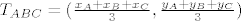 ( za trokut ABC ) i ( za trokut ABC ) i
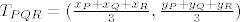 ( za trokut PQR ). ( za trokut PQR ).
Tvrdnja koju želimo dokazati :
Ako 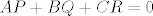 , onda , onda  . .
Tvrdnja se dokazuje direktno.
Pretpostavka: 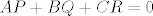 . .
Zapišimo dani izraz u sljedećem obliku:
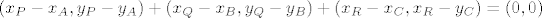 . .
Dvije točke su jednake ako su im pripadajuće koordinate jednake:
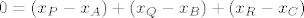
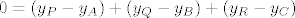 . .
Koristeći svojstva zbrajanja, zapišimo u obliku:
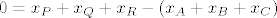
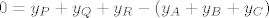 . .
Dodajmo 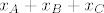 prvoj jednadžbi i prvoj jednadžbi i
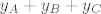 drugoj jednadžbi: drugoj jednadžbi:
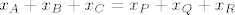 i i
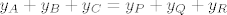 . .
Podijelimo dane jednadžbe s 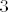 : :
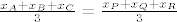 i i
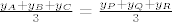 . .
Dvije točke su jednake kada su im pripadajuće koordinate jednake:
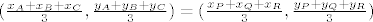 . .
Što možemo zapisati na sljedeći način:
 . .
Ukoliko sam negdje pogriješio, nadam se da će netko tu pogrešku ispraviti.
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
sequestered
Forumaš(ica)

Pridružen/a: 26. 06. 2011. (20:50:28)
Postovi: (4)16
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 23:54 ned, 30. 10. 2011 Naslov: Postano: 23:54 ned, 30. 10. 2011 Naslov: |
    |
|
|
Zapravo je zadatak vrlo trivijalan. Ako točka [tex]O[/tex] leži na dužini [tex]\overline{AB}[/tex] te ako je [tex]|OA| = |OB|[/tex], to znači da je točka [tex]O[/tex] polovište dužine [tex]\overline{AB}[/tex]. Kako vrijedi [tex]|OA| = |OB| = |OC| = r[/tex], to možemo konstruirati kružnicu [tex]k(O, r)[/tex]. S obzirom da je [tex]\overline{AB}[/tex] promjer te kružnice, a točka [tex]C[/tex] leži na kružnici [tex]k(O, r)[/tex], onda po teoremu o obodnom i središnjem kutu zaključujemo da je [tex]\triangle ABC[/tex] pravokutan sa pravim vrhom u kutu [tex]C[/tex].
Malo sam ja to raspisao......ali je dovoljno reći: zaključak slijedi iz Talesovog teorema: obodni kut konstruiran nad promjerom kružnice je pravi kut.
Zapravo je zadatak vrlo trivijalan. Ako točka [tex]O[/tex] leži na dužini [tex]\overline{AB}[/tex] te ako je [tex]|OA| = |OB|[/tex], to znači da je točka [tex]O[/tex] polovište dužine [tex]\overline{AB}[/tex]. Kako vrijedi [tex]|OA| = |OB| = |OC| = r[/tex], to možemo konstruirati kružnicu [tex]k(O, r)[/tex]. S obzirom da je [tex]\overline{AB}[/tex] promjer te kružnice, a točka [tex]C[/tex] leži na kružnici [tex]k(O, r)[/tex], onda po teoremu o obodnom i središnjem kutu zaključujemo da je [tex]\triangle ABC[/tex] pravokutan sa pravim vrhom u kutu [tex]C[/tex].
Malo sam ja to raspisao......ali je dovoljno reći: zaključak slijedi iz Talesovog teorema: obodni kut konstruiran nad promjerom kružnice je pravi kut.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
 Postano: 20:52 uto, 3. 1. 2012 Naslov: Postano: 20:52 uto, 3. 1. 2012 Naslov: |
    |
|
|
Može pomoć oko ovog zadatka? Tvrdnju treba dokazati koristeći metode analitičke geometrije.
[quote]Neka su F1, F2 fokusi, A i B glavna tjemena elipse (F1 je bliži tjemenu A) te P točka na elipsi različita
od A i B. Neka kružnica upisana trokutu F1F2P dodiruje AB u točki Q. Dokažite da je |AQ| = |F1P| i
|BQ| = |F2P|.[/quote]
Ja sam mislio to riješiti ovako: F1P,F2P i x-os su tangente kružnice, pa se pomoću uvjeta za dodir dobiju 4 rješenja (upisana i 3 pripisane kružnice) i zatim Q nađem kao presjek upisane kružnice i x-osi. I zatim pronađem zadane udaljenosti i pokažem da su jednake.
Međutim, trebalo bi mi previše vremena da se izvučem iz svih tih silnih jednadžbi i nepoznanica i varijabli, pa ako netko smisli neki jednostavniji (ili brži) način, slobodno prokomentira.
Hvala.
Može pomoć oko ovog zadatka? Tvrdnju treba dokazati koristeći metode analitičke geometrije.
| Citat: | Neka su F1, F2 fokusi, A i B glavna tjemena elipse (F1 je bliži tjemenu A) te P točka na elipsi različita
od A i B. Neka kružnica upisana trokutu F1F2P dodiruje AB u točki Q. Dokažite da je |AQ| = |F1P| i
|BQ| = |F2P|. |
Ja sam mislio to riješiti ovako: F1P,F2P i x-os su tangente kružnice, pa se pomoću uvjeta za dodir dobiju 4 rješenja (upisana i 3 pripisane kružnice) i zatim Q nađem kao presjek upisane kružnice i x-osi. I zatim pronađem zadane udaljenosti i pokažem da su jednake.
Međutim, trebalo bi mi previše vremena da se izvučem iz svih tih silnih jednadžbi i nepoznanica i varijabli, pa ako netko smisli neki jednostavniji (ili brži) način, slobodno prokomentira.
Hvala.
|
|
| [Vrh] |
|
|







