| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 12:49 sri, 11. 1. 2012 Naslov: |
    |
|
|
Ako ja kuzim oznake ovdje, onda tu nesto ne stoji: lijevo je broj (euklidska norma vektora je realni broj, a skalarni produkti vektora su realni ili kompleksni brojevi, ovisno o samim vektorima), a desno linearna kombinacija vektora x i y.
Ako ja kuzim oznake ovdje, onda tu nesto ne stoji: lijevo je broj (euklidska norma vektora je realni broj, a skalarni produkti vektora su realni ili kompleksni brojevi, ovisno o samim vektorima), a desno linearna kombinacija vektora x i y.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)
Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
| Postano: 14:33 sub, 14. 1. 2012 Naslov: |
|
|
|
Za dobivanje ortonormirane baze koristiš Gramm-Schmidtov postupak ortogonalizacije, već je rađeno na vježbama i u linearnoj 2, skalarni produkt ti je definiran tim integralom...ortonormiraj prvo 1, zatim t pa[tex]t2[/tex]...
ortogonalna projekcija polinoma će biti ort.proj.=(p|e1)e1 +(p|e2)e2 + (p|e3)e3 pri čemu je p-zadani polinom a e1,e2,e3 ortonormirana baza...
Za 5. zad dovoljno je dobiti lambda na 50 što se lako vidi iz razlike kvadrata da je (-1) i 1 pa po teoremu o spektru i funkciji operatora doći ćeš do traženog, također sličan primjer rađen na vježbama....
Nadam se da je objašnjenje razumljivo...
[/tt][/strike][/quote]
Za dobivanje ortonormirane baze koristiš Gramm-Schmidtov postupak ortogonalizacije, već je rađeno na vježbama i u linearnoj 2, skalarni produkt ti je definiran tim integralom...ortonormiraj prvo 1, zatim t pa[tex]t2[/tex]...
ortogonalna projekcija polinoma će biti ort.proj.=(p|e1)e1 +(p|e2)e2 + (p|e3)e3 pri čemu je p-zadani polinom a e1,e2,e3 ortonormirana baza...
Za 5. zad dovoljno je dobiti lambda na 50 što se lako vidi iz razlike kvadrata da je (-1) i 1 pa po teoremu o spektru i funkciji operatora doći ćeš do traženog, također sličan primjer rađen na vježbama....
Nadam se da je objašnjenje razumljivo...
[/tt][/strike][/quote]
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)
Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)
Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol:
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
| Postano: 13:51 čet, 26. 1. 2012 Naslov: |
|
|
|
[quote="kkarlo"][quote="slonic~tonic"]kad trazimo najbolju aproksimaciju, moramo li odrediti matricu ili napisati zbroj pomocu matrica ortonormirane baze ??[/quote]
Odrediti matricu.
Barem je asistentica Prlic dala za rjesenje 5. zadatka iz domace zadace matricu...[/quote]
hvala! :)
nesto me zbunjuje :S..
kad odredujemo adjungirani operator operatora
A(x1, x2) = (2x1, ix1-x2)
je li rjesenje
A*(x1, x2) = (2x1, -ix1-x2), ko sto je odredeno na vjezbama, ili
A*(x1, x2) = (2x1 + ix2, -x2) gdje sam racunala prema postupku iz la2.. :/
| kkarlo (napisa): | | slonic~tonic (napisa): | | kad trazimo najbolju aproksimaciju, moramo li odrediti matricu ili napisati zbroj pomocu matrica ortonormirane baze ?? |
Odrediti matricu.
Barem je asistentica Prlic dala za rjesenje 5. zadatka iz domace zadace matricu... |
hvala! 
nesto me zbunjuje :S..
kad odredujemo adjungirani operator operatora
A(x1, x2) = (2x1, ix1-x2)
je li rjesenje
A*(x1, x2) = (2x1, -ix1-x2), ko sto je odredeno na vjezbama, ili
A*(x1, x2) = (2x1 + ix2, -x2) gdje sam racunala prema postupku iz la2.. 
_________________
Lakše je naučiti matematiku nego raditi bez nje.
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)
Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol:
|
| Postano: 14:17 čet, 26. 1. 2012 Naslov: |
|
|
|
[quote="slonic~tonic"][quote="kkarlo"][quote="slonic~tonic"]kad trazimo najbolju aproksimaciju, moramo li odrediti matricu ili napisati zbroj pomocu matrica ortonormirane baze ??[/quote]
Odrediti matricu.
Barem je asistentica Prlic dala za rjesenje 5. zadatka iz domace zadace matricu...[/quote]
hvala! :)
nesto me zbunjuje :S..
kad odredujemo adjungirani operator operatora
A(x1, x2) = (2x1, ix1-x2)
je li rjesenje
A*(x1, x2) = (2x1, -ix1-x2), ko sto je odredeno na vjezbama, ili
A*(x1, x2) = (2x1 + ix2, -x2) gdje sam racunala prema postupku iz la2.. :/[/quote]
Neznam koji je to postupak iz la2, ali ovaj sa vjezbi je sigurno tocan rezultat.
Mislim, logicno je, prvo nadjemo zapis u npr kanonskoj bazi, jer nam je kasnije lakse za racunat, i onda napravimo komplement i transponiramo je, i vratimo nazad na x1 i x2...
Neznam, probaj opisati postupak koji si ti radila po la2 pa mozda skuzimo gdje je greska...Morala bi dobit isto kosto smo dobili na vjezbama.
| slonic~tonic (napisa): | | kkarlo (napisa): | | slonic~tonic (napisa): | | kad trazimo najbolju aproksimaciju, moramo li odrediti matricu ili napisati zbroj pomocu matrica ortonormirane baze ?? |
Odrediti matricu.
Barem je asistentica Prlic dala za rjesenje 5. zadatka iz domace zadace matricu... |
hvala!
nesto me zbunjuje :S..
kad odredujemo adjungirani operator operatora
A(x1, x2) = (2x1, ix1-x2)
je li rjesenje
A*(x1, x2) = (2x1, -ix1-x2), ko sto je odredeno na vjezbama, ili
A*(x1, x2) = (2x1 + ix2, -x2) gdje sam racunala prema postupku iz la2.. |
Neznam koji je to postupak iz la2, ali ovaj sa vjezbi je sigurno tocan rezultat.
Mislim, logicno je, prvo nadjemo zapis u npr kanonskoj bazi, jer nam je kasnije lakse za racunat, i onda napravimo komplement i transponiramo je, i vratimo nazad na x1 i x2...
Neznam, probaj opisati postupak koji si ti radila po la2 pa mozda skuzimo gdje je greska...Morala bi dobit isto kosto smo dobili na vjezbama.
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
| Postano: 15:04 čet, 26. 1. 2012 Naslov: |
|
|
|
[quote="kkarlo"][quote="slonic~tonic"][quote="kkarlo"][quote="slonic~tonic"]kad trazimo najbolju aproksimaciju, moramo li odrediti matricu ili napisati zbroj pomocu matrica ortonormirane baze ??[/quote]
Odrediti matricu.
Barem je asistentica Prlic dala za rjesenje 5. zadatka iz domace zadace matricu...[/quote]
hvala! :)
nesto me zbunjuje :S..
kad odredujemo adjungirani operator operatora
A(x1, x2) = (2x1, ix1-x2)
je li rjesenje
A*(x1, x2) = (2x1, -ix1-x2), ko sto je odredeno na vjezbama, ili
A*(x1, x2) = (2x1 + ix2, -x2) gdje sam racunala prema postupku iz la2.. :/[/quote]
Neznam koji je to postupak iz la2, ali ovaj sa vjezbi je sigurno tocan rezultat.
Mislim, logicno je, prvo nadjemo zapis u npr kanonskoj bazi, jer nam je kasnije lakse za racunat, i onda napravimo komplement i transponiramo je, i vratimo nazad na x1 i x2...
Neznam, probaj opisati postupak koji si ti radila po la2 pa mozda skuzimo gdje je greska...Morala bi dobit isto kosto smo dobili na vjezbama.[/quote]
dakle, znamo da vrijedi (Ax, y) = (x, A*y).
(Ax, y) = ((2x1, ix1-x2), (y1, y2)) = 2x1y1 + ix1y2 - x2y2 = x1(2y1 + y2) + x2(-y2) = ((x1, x2), (2y1 + iy2, -y2))
i zatim, buduci da je A nad C => A*(x1, x2) = (2x1 - ix2, -x2)
| kkarlo (napisa): | | slonic~tonic (napisa): | | kkarlo (napisa): | | slonic~tonic (napisa): | | kad trazimo najbolju aproksimaciju, moramo li odrediti matricu ili napisati zbroj pomocu matrica ortonormirane baze ?? |
Odrediti matricu.
Barem je asistentica Prlic dala za rjesenje 5. zadatka iz domace zadace matricu... |
hvala!
nesto me zbunjuje :S..
kad odredujemo adjungirani operator operatora
A(x1, x2) = (2x1, ix1-x2)
je li rjesenje
A*(x1, x2) = (2x1, -ix1-x2), ko sto je odredeno na vjezbama, ili
A*(x1, x2) = (2x1 + ix2, -x2) gdje sam racunala prema postupku iz la2.. |
Neznam koji je to postupak iz la2, ali ovaj sa vjezbi je sigurno tocan rezultat.
Mislim, logicno je, prvo nadjemo zapis u npr kanonskoj bazi, jer nam je kasnije lakse za racunat, i onda napravimo komplement i transponiramo je, i vratimo nazad na x1 i x2...
Neznam, probaj opisati postupak koji si ti radila po la2 pa mozda skuzimo gdje je greska...Morala bi dobit isto kosto smo dobili na vjezbama. |
dakle, znamo da vrijedi (Ax, y) = (x, A*y).
(Ax, y) = ((2x1, ix1-x2), (y1, y2)) = 2x1y1 + ix1y2 - x2y2 = x1(2y1 + y2) + x2(-y2) = ((x1, x2), (2y1 + iy2, -y2))
i zatim, buduci da je A nad C ⇒ A*(x1, x2) = (2x1 - ix2, -x2)
_________________
Lakše je naučiti matematiku nego raditi bez nje.
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)
Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol:
|
| Postano: 20:14 čet, 26. 1. 2012 Naslov: |
|
|
|
Cemu kompliciranje? :blista:
[latex]A=\begin{bmatrix} 2 & 0 \\ i & -1 \end{bmatrix}[/latex]
Zatim konjugiras i transponiras (BTW, ti si zaboravila konjugirati)
[latex]A^*=\begin{bmatrix} 2 & -i \\ 0 & -1 \end{bmatrix}[/latex]
[size=9][color=#999999]Added after 18 minutes:[/color][/size]
[quote="slonic~tonic"][quote="Swerz"]Nilpotentan operator u spektru ima samo 0, dok regularni nema 0.
Dakle, operator nije ni nilpotentan ni regularan. (ukoliko si dobro izracunao spektar)[/quote]
e hvala :) shvatila sam :)[/quote]
E krivo si shvatila jer ti je netko krivo pojasnio :D
Daklem, pozivas se na tm o preslikavanju spektra...
Uvrstavas sv. vrijednosti iz zadanog spektra {-3, 0, 2} u [latex]tg(\frac{\pi}{4}sin(\frac{\pi}{2}A))[/latex] i dobijes redom {1, 0, 0}, ilitiga {1,0}. I onda zakljucis da operator nije nilpotentan, a bogami ni regularan :D
Cemu kompliciranje? 
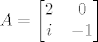
Zatim konjugiras i transponiras (BTW, ti si zaboravila konjugirati)
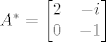
Added after 18 minutes:
| slonic~tonic (napisa): | | Swerz (napisa): | Nilpotentan operator u spektru ima samo 0, dok regularni nema 0.
Dakle, operator nije ni nilpotentan ni regularan. (ukoliko si dobro izracunao spektar) |
e hvala shvatila sam |
E krivo si shvatila jer ti je netko krivo pojasnio 
Daklem, pozivas se na tm o preslikavanju spektra...
Uvrstavas sv. vrijednosti iz zadanog spektra {-3, 0, 2} u 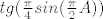 i dobijes redom {1, 0, 0}, ilitiga {1,0}. I onda zakljucis da operator nije nilpotentan, a bogami ni regularan
_________________
Though your dreams be tossed and blown...
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
| Postano: 20:19 čet, 26. 1. 2012 Naslov: |
|
|
|
[/quote]
E krivo si shvatila jer ti je netko krivo pojasnio :D
Daklem, pozivas se na tm o preslikavanju spektra...
Uvrstavas sv. vrijednosti iz zadanog spektra {-3, 0, 2} u [latex]tg(\frac{\pi}{4}sin(\frac{\pi}{2}A))[/latex] i dobijes redom {1, 0, 0}, ilitiga {1,0}. I onda zakljucis da operator nije nilpotentan, a bogami ni regularan :D[/quote]
ma ne ne, to sam znala i prije :D..samo nisam znala odrediti da li je regularan ili nilpotentan..tj nisam znala kad je regularan :oops: :oops: ...
ali hvala ;)
[/quote]
E krivo si shvatila jer ti je netko krivo pojasnio
Daklem, pozivas se na tm o preslikavanju spektra...
Uvrstavas sv. vrijednosti iz zadanog spektra {-3, 0, 2} u 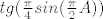i dobijes redom {1, 0, 0}, ilitiga {1,0}. I onda zakljucis da operator nije nilpotentan, a bogami ni regularan [/quote]
ma ne ne, to sam znala i prije ..samo nisam znala odrediti da li je regularan ili nilpotentan..tj nisam znala kad je regularan  ...
ali hvala 
_________________
Lakše je naučiti matematiku nego raditi bez nje.
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)
Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol:
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)
Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol:
Lokacija: pod stolom
|
|
| [Vrh] |
|
cocco
Forumaš(ica)
Pridružen/a: 21. 01. 2010. (22:06:02)
Postovi: (4D)16
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)
Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol:
Lokacija: pod stolom
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)
Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol:
|
|
| [Vrh] |
|
|
