Ovaj zadatak je loše sročen i fale neke informacije koje su potrebne da bi se uopće odredilo o kojem liku se radi. Prvo, presjek y=-0.5 i y=-sinx nije lik. To su točke [latex](\frac\pi 6+2k\pi,-1/2)[/latex] i [latex](\frac{5\pi}{6}+2k\pi,-1/2)[/latex]. Kada se te točke zarotiraju oko x-osi dobiju se kružnice, a one nemaju volumen.
Drugo, ne zna se s koje strane pravca y=-1/2 je omeđen taj lik, tj. da li je omeđen s y=0 i y=-1/2 ili s y=-1/2 i y=-1.
Treće, taj volumen je beskonačan jer nema ograničenja na x. U slučaju da je ploha omeđena s [latex]x=0[/latex], [latex]x=\pi[/latex], [latex]y=0[/latex] i [latex]y=-1/2[/latex], onda bi volumen tijela određenog rotacijom grafa funkcije [dtex]y(x)=\left\{
\begin{array}{rl}
-\sin{x}, & 0\leq x < \frac\pi 6,\\
-1/2, & \frac\pi 6 \leq x \leq \frac{5\pi}{6},\\
-\sin{x}, & \frac{5\pi}{6}<x\leq\pi
\end{array}
\right.[/dtex]
oko osi x izračunali integriranjem
[dtex]V=\pi\int_0^\pi y(x)^2 dx=\pi\int_{0}^\frac{\pi}{6}\sin^2 x dx+\pi\int_{\frac{\pi}{6}}^\frac{5\pi}{6}\frac 14 dx+\pi\int_{\frac{5\pi}{6}}^\pi\sin^2 x dx.[/dtex]
Ovaj zadatak je loše sročen i fale neke informacije koje su potrebne da bi se uopće odredilo o kojem liku se radi. Prvo, presjek y=-0.5 i y=-sinx nije lik. To su točke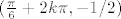 
i 
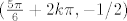. Kada se te točke zarotiraju oko x-osi dobiju se kružnice, a one nemaju volumen.
Drugo, ne zna se s koje strane pravca y=-1/2 je omeđen taj lik, tj. da li je omeđen s y=0 i y=-1/2 ili s y=-1/2 i y=-1.
Treće, taj volumen je beskonačan jer nema ograničenja na x. U slučaju da je ploha omeđena s 
, 
, 
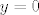i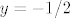 
, onda bi volumen tijela određenog rotacijom grafa funkcije [dtex]y(x)=\left\{
\begin{array}{rl}
-\sin{x}, & 0\leq x < \frac\pi 6,\\
-1/2, & \frac\pi 6 \leq x \leq \frac{5\pi}{6},\\
-\sin{x}, & \frac{5\pi}{6}<x\leq\pi
\end{array}
\right.[/dtex]
oko osi x izračunali integriranjem
[dtex]V=\pi\int_0^\pi y(x)^2 dx=\pi\int_{0}^\frac{\pi}{6}\sin^2 x dx+\pi\int_{\frac{\pi}{6}}^\frac{5\pi}{6}\frac 14 dx+\pi\int_{\frac{5\pi}{6}}^\pi\sin^2 x dx.[/dtex]
_________________
The Dude Abides
.
